Math Olympiad | Find the area of semicircle inside a square | 2 Different Methods
HTML-код
- Опубликовано: 20 апр 2024
- Math Olympiad | Find the area of semicircle inside a square | 2 Different Methods
MY OTHER CHANNELS
••••••••••••••••••••••••••••••••
Calculus Booster : / @calculusbooster
Math Hunter : / @mathshunter
--------------------------------------------------------------------------------
Join the channel to become a member
/ @mathbooster








I now have a question: wouldn't the second method be simplified by the two tangent theorem? I came across a PreMath video that tackles that similar problem.
I love learn math with you
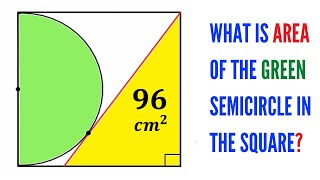
3rd and the easiest solution:
Draw |OQ| line, which is the radius r of the semi circle.
Since the angles APD, PAB, QOC are equal, AQOB and OQPC are similar deltoids.
[PC] can be calculated using similarity: [AB] / [OC] = [QO] / [PC].
So, [PC] = r.r/2.r => [PC]=r/2
Area of triangle=|AD|.|DP|.1/2
6 = 2r.(2r-r/2).1/2
6 = r.3r/2
4 = r²
semicircle area = 4.π/2 = 2π
old but gold here ;)
Nice!
Let α the side of the square ABCD => α=2R and DP=x.
Obviously PC=α-x
AB=AQ=α ( tangent segments from A) and PQ=PC=α-x (tangent segments from P)
AP=AQ+QP=α+α-x=> *AP=2α-x*
Area of triangle ADP =6 => 1/2 AD⋅DP=6=> 1/2 α⋅x=6 => *αx=12* (1)
Pythagoras theorem in orthogonal triangle ADP =>
AD²+DP²=AP²⇒α²+x²=(2α-x)²
α²+x²=4α²-4αx+x²
3α²-4αx=0
3α²-4⋅12=0 cause (1)
So α=4 and R=α/2=2
Area of the semicircle = (πR²)/2=(π⋅2²)/2=2π
By Peytaghoras Theorem
At 7:25, we have 8Rx = 4R². We can safely assume that R is not 0 and factor out R from both sides, leaving 8x = 4R and x = R/2. Now we return to 6 = 2R² - xR and substitute R/2 for x, leaving 6 = 2R² - (R/2)R = 2R² - R²/2 = 3R²/2, (6)(2) = 3R², R² = 4. From there, proceed to calculate the area of the semicircle as (1/2)πR² = (1/2)π(4) = 2π.
An interesting observation can be made about right ΔADP. The lengths of the sides are AD = 4, DP = 3 and hypotenuse AP = 5. So, its sides form the Pythagorean triple 3-4-5. If the area of right ΔADP is changed, the new triangle will be similar to a 3-4-5 right triangle. The ratio of area of the ΔADP to the semicircle will remain 6:2π = 3:π
Wow!!! Thanks for noticing 😊😊😊😊
Area of the semicircle=2π. Thanks ❤.
I love math ❤❤
LOL. I'm embarrassed that it took me almost the entire video to see that PQ = PC, even though I knew easily that AB = AQ. I just couldn't see it!
Same here.
Golly the first method seems to be a lot easier
φ = 30°; ∎ABCD → AB = BC = BO + CO = a/2 + a/2 = r + r = CD = CP + DP = AD = a
AP = AQ + PQ; sin(OBA) = sin(AQO) = sin(POA) = sin(OQP) = sin(3φ) = 1; area ∆ ADP = 6
BAO = OAQ = COP = POQ = ϑ → sin(ϑ) = √5/5 → cos(ϑ) = 2√5/5 → tan(ϑ) = 1/2 →
CP = a/4 → DP = 3a/4 → (1/2)(3a/4)a = 6 → a = 4 → a/2 = 2 = r → area semi circle = 2π
asnwer=35cm