Second fundamental theorem and chain rule | MIT 18.01SC Single Variable Calculus, Fall 2010
HTML-код
- Опубликовано: 6 фев 2025
- Second fundamental theorem and chain rule
Instructor: Christine Breiner
View the complete course: ocw.mit.edu/18-...
License: Creative Commons BY-NC-SA
More information at ocw.mit.edu/terms
More courses at ocw.mit.edu
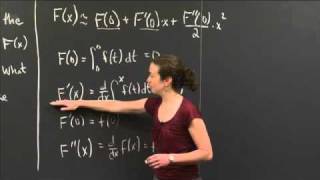

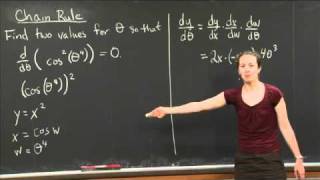






This lady explained in 5 minutes what my teacher failed to explain in 5 days.
in my case, she never explained it XD
the whole semester LOL
@@its_reckoning6667 LMAO
Search mohit tyagi sir in youtube that have done more hard problems on the concept of derivqtive of integration
@@yeonhojung7185 xD
This explanation was simply beautiful. Very well understanding of the proof.
Thanks Christine and Joel. I took this stuff many, many moons ago. Now that I'm retired I'm revisiting it all. The current political climate serves notice that math and science matter; now more than ever. I wish RUclips in general and these 'tutoials' in particular had been around back in the day. It would have made learning a little less painful. Thanks again.
MIT has the nicest chalk borads
Wow that made so much sense. That explanation was spot on.
This was one of the most difficult things to figure out on my own so far in calc 1. I don't know why. But this video was so clear and concise, I can't believe I didn't know how to do this before. Fantastic work.
never thought i would gain a better understanding from an MIT lecture but thanks
Thanks for teaching me like math like the way a chef would.
Got some serious chalk over there at MIT
beautiful explanation, beautiful usage of chalk, this is my favorite video on youtube.
Professor Breiner ,thank you for another fine explanation of the Second Fundamental Theorem of Calculus and the Chain Rule.
Life Saver!
That is pure genius!
Great explanation, concise example.
Thank you for going over this. It seems most books and lectures brush over this concept. You nailed it with this video.
For any Calc 1 students, this is CALCULUS 10e, by Larson, p285, Example 8. The book doesnt do a very good job of explaining this concept. Watch this video, it will save you a giant headache.
Wow! I'm gonna look for more lectures by Christine Breiner.
Dear madam, thank you very much for clear explanation
Thank you!!! I can actually do my calculus homework now!
amazing explanation!
I feel like profs are able to explain in five mins like her but they purposely drag out the class because they have to
Simple and to the point. Thank you.
WHAT A great explanation
i love MIT
Elegantly explained! Thank you!
Thanks MIT. Appreciate your videos and your competent and intelligent instructors.
continuity is not sufficient for differentiability, it is necessary. Investigating differentiability is not a trivial thing to do. ITs a must do thing. ITs like starting swimming without knowing if you can swim.
Thanks christin
this goddess upon earth just explained what a $200 textbook and a $200,000 tenured professor failed to explain. please give her all the mansions and gold
megan fox = 2.5/10, this woman = 12/10
Thank you 🌷🏵
I Really Like The Video Second fundamental theorem and chain rule From Your
really wonderful nd awesome. sweet voice. very appealing to a new learner.
Man, she made that look easy.
silentthriller its easy cause you understand now how to do it
excellent!
why was the lower limit of the integral not evaluated? I thought answer should be 2xcosx2 -cos0
I guess, let t=x ie dx=dt and gives cosx as integral fn and upon integration gives sinx and then we put limits to get sinx^2, and then applying d/dx to give same answer as, 2xcosx^2.😊😊
Don't get this at all. I thought the bounds, when in terms of x were just ' dummy variables' that replaced t, in this example, don't see why the chain rule is needed in all of this.
what if we have the two bounding values as functions of x ?
thanks!
Why can we ignore the lower bound here? Shouldn't it be evaluated? I get for Sin(x) that value is 0, but don't we have to subtract 1 at some point here?
FTC2 isn't concerned with calculating the definite integral as with FTC1 (F(b) - F(a)). FTC 2 says the output of a definite integral with respect to t, lower limit fixed at a and variable upper limit x is F(x), and that F'(x) = f(x) (which is NOT f(t)). And for some reason they always want us to find the derivative of F(x). Nobody has told us why we'd want to do that. But obviously it would be the integrand of the original integral but with an 'x' argument rather than a 't' argument. And here she shows us that we'd need to apply the chain rule if the upper limit of integration was actually a function of x and not just x. Another point about the lower limit of integration 'a' and F: it's baked in to F, which calculates the area under f(t) between a and whatever ends up being x. That is, if you pass 'a' to F it will always be zero because when you pass an argument to F it's always in the role of the upper limit of integration. If the lower limit of integration is the same as the upper limit, as you may recall, you always get zero (think graphically you would be looking for the area under f(t) between a and a which is of course zero). Also consider that If you had a definite integral for some intervals of t^2, F(x) would be a third degree polynomial whose y values indicate the area under t^2, and the graph would always equal zero at a.
What if your lower limit is x instead of 0? So we have d/dx integral ( cos t dt ) on [ x, x^2]
int from x to x^2 = int from x to a + int from a to x^2 = - int from a to x + int from a to x^2
I bit late but if integer from x to x^2 = int from 0 to x^2 - int from 0 to x
==> d/dx( int from x to x^2 of f(x) dx)
= F ' (x^2)2x - F'(x)
@@demr04 A bit late! 7 years late 😅
@@thebagelboyjr9351 I came with the milk tho
Wouldn't it be easier to evaluate de definite integral, and then just deriving it..?
I thought you also had to take the derivative of Cosine?
AMAZING
Why the derivative of cos is still cos?
mathematics is not formulas. Next time before applying formulas and talking about chain rules wud be nice to introduce to kids the fact that both functions are differentiable even if it is trivial to show.
she is not explained using the limits of different variables
how would I solve such a question when the function inside integral be something like (f(t)/t)dt?
But why does it work. Can i get a proff for this.Thanks.
how did we know that F'x= cosx?
1st FTC.
I have never been more confused. 600 sq. ft. of slate, a 2x4 for a piece of chalk, and she starts beating the slate with the 2x4. When I finally recovered from the distraction, she said something about how she wants us to understand there is a much bigger, underlying problem.
NO KIDDING!!!
madam please make me understand first theorem if calculus
Kids go to MIT for the CHALK
only Chuck Norris would be able to solve it between 0:23 - 0:28
They still use chalk at MIT?
A lot of math teachers/professors in particular prefer chalk
@@chilbopro right on
I like chalk
I want ti gi ti MIT
Your solution is very hard to understand.
i didnt hear shit except look at the chalk damnn
Yay for learning! And she's a damn cute mathematician ;).
my math teacher deserve to be paid better ..he is better than her .