Half Derivative of x
HTML-код
- Опубликовано: 9 фев 2025
- You may be familiar with derivatives, but do you know how to take half-derivatives? What does that even mean? In this video I define the concept of a half derivative, and then calculate the half-derivative of x^n, and then show what that result is for x. The answer may surprise you, or maybe not :P
Sequel: • Half derivative of cos x


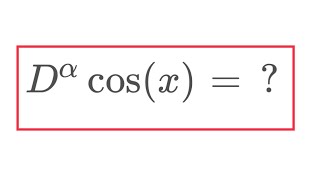






Here’s a link to the sequel: Fractional derivatives of exponential and trigonometric functions
ruclips.net/video/k2T0YilPrWw/видео.html
Some applications of fractional derivatives:
There are surprisingly many applications of this, because it turns out that some differential equations in physics are written in terms of fractional derivatives, see en.wikipedia.org/wiki/Fractional_calculus#Applications
There are three other ones I can think of:
1) In functional analysis, it's an important problem to find a square root of an operator (I don't really know why, maybe to decompose that operator?), and what we really did is to find a square root of the derivative operator, because if you apply D1/2 twice, you get D, so (D1/2)^2 = D, so D1/2 = sqrt(D) in some sense.
2) There is the nice formula in Fourier analysis that says that the Fourier transform of f' is integral of x e^(i something), and we have a similar formula for the fractional derivative, (I think, don't quote me on that) that the Fourier transform of D^(1/2) f is integral of x^(1/2) e^(i something).
3) Fractional derivatives allow us to define nice spaces of functions (for example, those whose fractional derivatives exist and are square integrable), and sometimes in differential equations you have a solution that is not defined in the classical sense (i.e. continuously differentiable), but might belong to this nice space, which allows us to study those equations.
so what would that mean you can have a ith derivative
In electronic filtering applications, an integrator may be used as a low-pass filter that attenuates signals by ~6dB/octave (a factor of two in amplitude for a factor of two in frequency) and a differentiator may be be used as a 6dB/octave high-pass filter. Integration and differentiation thus behaves as filters whose amplitude/frequency function, plotted on a log/log scale, would have slopes of -1 and +1, respectively. I would expect that non-generalized derivatives and integrals would behave as filters whose slope on a log/log scale is the order of the derivative.
2=1+1
7=4+3
Prove 1+1 is 2 or site Cantor`s proof. Doc P can frCTIONAL DERIVATIVES BE DEFINEd using Fourier pseudodiff operators? If so do a video. TIA
*gives blackpenredpen a cookie* (Oreo brand, of course.)
2+2=5
and 1+1=2 communicative property of addition don't forget that either
It now seems obvious that not all derivatives should be positive integers. In fact, when you think about it, negative derivatives are integral to math and science
PCreeper394 god damnit
OH MAN HAD TO READ THAT THRICE BECAUSE I KNEW I WAS MISSING SOMETHING
let's try complex derivatives
@@OfficialMrQ That could be complex
a+b
1:25 Maan, you're gonna kill me with high-level mathematics.
I'm not ready for Ph.D. level math yet! I'm still in high school!
If I watch this video while half asleep, and watch it again while half asleep, will I have watched it in my sleep?
Hahaha, they say that sleeping is addi(c)tive! :P
Never realized how mathematical a bed can be. Multiplication _and_ addi(c)tion?
Hahaha, a bed is an algebra then 😂
What I learned today: 2=1+1. Thanks Dr. Peyam!
I did too!!
i learned today that 2=bprp+dr. peyam
i love '2' !!!
but also that 2≠½+1+½
and 7 = 4 + 3
Your enthusiasm about this beautiful art is contagious, sir. You are amazing.
"A derivative is a derivative, you can't say it's only a half"
Joking aside, really great video
Lmao
As soon as I saw this video I looked for this comment.
Well Dr """"""""""Peyam"""""""" yoshi.
God tier coment
Is this a half video TOO !
Now do the half-integral !
Poetu Hahaha, great idea!!! :D I'm guessing it should be constant times x^3/2 :)
OMG, guess what!!! If you assume that the half-derivative of the half-integral of a function is just the function itself, then:
Claim: The half-integral of a function is just the half derivative of the ordinary integral! Here's why:
By definition, the half integral int^(1/2) should satisfy:
int^(1/2) (int^(1/2) f) = int f (the integral of f)
Now take half derivatives on both sides:
D^(1/2) int^(1/2) (int^(1/2) f) = D^(1/2) int f
Now assuming that the half derivative of the half integral of a function is just the function itself, we then get
int^(1/2) f = D^(1/2) (int f)
Ta-daa!!!! :D
Dr. Peyam's Show amazing!
I totally read that in your voice
Remember, if you do the half integral, make sure you only add C/2 at the end!
I am super excited to watch this video, because actually I have thought about this concept of non-interger order derivatives some years ago, when I was like 16 or so. However I obviously didn't have the tools nor the knowledge to actually develop the idea. But know I'm watching someone who thought about this like I did! Amazing!
Hell, I did the same thing, but I looked up the gamma function, tried to read the Wikipedia article, and gave up.
I was thinking about negative-order derivative
Alexander Fadeev there would be integrals. I think Peyam shows this in other video or in this one. The point is that if the derivative of f is D^1(f), then considering that the grade of the derivative is equal to the sum of the "exponents", and that any function is its own 0th derivative, then D^-1(D^1(f)) = f. Considering the fundamental theorem of calculus, of derive a function and then integrate it you get the original function. Also, considering that integration also satisfies the linear transformation properties, we can assume that D^-1(f) is the integral of f. (Technically you also have a constant of integration, but I've neglected it for demonstration purposes)
SAME. Me too, I considered it as he did but wasn’t thinking about the linearity thing and never tried one.
R u Indian?
Both you and blackpenredpen rock! Keep those awesome math videos coming!
Thanks so much!!! bprp and I really appreciate it!!!
Thanks!!!
Is it blackpenredpen that I can hear in the background? Edit: err probably since he commented on this comment lol...
roygalaasen loll yes.
This is the quality content I came here for. Please explore the properties of non-integer derivatives of some non-polynomials!
RUclips started this rabbit hole for me, and I’m glad it finally brought me to the video that has the best explanation I’ve seen so far!
this dude is just filled to the brim with positive energy
A few years back, I thought of the idea of a half-derivative. I realized that sinx and e^x work quite well, being sin(x + pi/4) and e^x. The only thing was, I almost felt like people would laugh at me for proposing something so ridiculous. Of course now I'm actually quite relieved to see that at least one other person was just as crazy as me, and I kinda wish I wouldn't have convinced myself that it having no apparent application it was useless. I mean like a lot of math was discovered before it was needed, so... I think I should probably finally figure out the half-derivative chain rule.
"A derivative is a derivative. You can't say it's only a half." - TJ Henry Yoshi
Computer pannenkoek2012 heck yes
Your excitement is contagious. Love your personality.
I just learnt derivatives in School and watched this entirely video without getting a single thing and enjoyed the hell out of it only from watching the hype and excitement. Wished i had you as a teacher xD. Keep it up ^^ :3
Dr Payem! What about negative derivatives, are they possible? Or is that an integral?
What about complex derivatives? (The i-th derivative of x)
Maybe this can be used to create some very hard differential equations.
This is an eye opener thanks for the amazing video.
Ahsoka Tano Indeed the -1th derivative of f is just the integral of f, because by definition we should have D(D-1 f) = f, and similarly the -alpha derivative of f is the integral of the alpha derivative of f. Not sure about complex numbers, but since Gamma is defined for complex numbers this might actually work! I'll check it out and see what happens, but I'm guessing it's just a constant times x^(1-i)
Ahsoka Tano Oh, and there are indeed differential equations with fractional derivatives! Check out one of the comments below where I put some applications!
Wait but wouldn't the kth derivative (where k is a negative natural number) not exist for x^n since that would yield a negative natural number in the gamma function, which isn't defined?
Dr Peyam yay
And yet, GermanSnipe14, we can very easily integrate x to obtain it's kth integrals (where k is positive natural number), so I think this generic definition of the derivative is incomplete, do we need to make a special gamma function so that it has satisfactory values?
This is only the first video of yours I've seen, but it's so dang good I had to subscribe!
Thanks so much!!!! :D
This was a fascinating video, it had everything: Derivatives, Gamma Function and the Gaussian Integral. Thank you Dr. Peyam!
Excellent explanation and presentation of the non-integer derivation of the monoms. I would have two other candidates for similar cases to examine: 1) You could take the taylor development of the square root and apply it to the derivative operator. 2) You could take the Fourier analysis of the function you want to derivate and then the n-th derivative of sin(omega x) is (omega^n)*sin(omega x + n*pi/2) and the n-th derivative of cos(omega x) is (omega^n)*cos(omega x + n*pi/2).
Check out my playlist, I do precisely that
For those wanting to read up on this subject, there is a book published by Dover Publications and authored by KB Oldham and J Spanier. It is a good introduction to the subject.
What's it called?
Here it is:
b-ok.cc/book/2315244/757a6e
@@RAJAT6555 Thank you so much...
Mind blowing half derivative.... of x
Simply amazing.
Dr. Peyam always master of mathematics
Thanks, Dr. Peyem! Very clear; each step made sense Now I need to think, re-view and internalize the whole thing! Then I'll be able to grin a Cheshire-cat-like grin, and know what I'm talking about.
Thanks for the kudos, Dr Peyam! The Cheshire Cat now awards himself a generous saucer of double cream.
This is great stuff! Never thought of the concept of fractional order derivatives, but it comes so naturally. Thanks Dr P!
Fun fact: It is not possible to extend that result to any continously differentiable function.
Why not? He claimed it is a linear operator so polynomials and power series are half-differentiable and thus so are all holomorphic functions which even though still doesnt cover all continuously differentiable functions it includes most elementary functions
turbo potato As an exercise try to calculate the half derivative of x->1 (this only requires basic linear algebra), this will lead to a contradiction.
Isn't "f(x)=x" a continuous, differentiable function? So the last result shown in the video is not valid?
Wait... what do you mean?
Thanks for supplying a little bit of actual math here.
I love how he always sneaks in pop culture references into his videos
This was soooooooo fucking legit
Thank you!!!
He is the happiest person I've ever seen.
Your video is cool! The half derivative of a function is really a great thing; I want to learn more about it. But, I want to know what is the geometrical interpretation of half derivative?
I have done so many proofs in Undergraduate Maths but I never enjoyed it. finding you I am enjoying learning mathematics.
Thank you Sir.
What a fun video. Interesting topic, and it was great to see you guys having so much fun with the maths. Subbed :)
2 =1+1
BPRP : LAUGHS LIKE CRAZY
Fast forward to 2019:
BPRP: 2=1+1
I'm just waiting for a practical use of this incredible and ridiculously complicated piece of art.
See the pinned comment for applications :)
That got a lot more tricky than I anticipated. Well played!
I nenver, ever imagine that this could be posible. Your channel is amazing.
Wow I really wonderred if there's any way to define derivative 'continuously' when I first knew the second and third derivative and this video answers my question in 20 mins! I really enjoyed this video and now I wonder how to define half derivative in analytic way. Thank you Dr. Peyam!!
This is amazing! 6 min in and im already impressed!
Incredibly amazed. Great video!!!
Thanks for the great video! Do you know of any applications of fractional derivatives? Why might someone want to calculate fractional derivatives?
There are surprisingly many applications of this, because it turns out that some differential equations in physics are written in terms of fractional derivatives, see en.wikipedia.org/wiki/Fractional_calculus#Applications
There are three other ones I can think of:
1) In functional analysis, it's an important problem to find a square root of an operator (I don't really know why, maybe to decompose that operator?), and what we really did is to find a square root of the derivative operator, because if you apply D1/2 twice, you get D, so (D1/2)^2 = D, so D1/2 = sqrt(D) in some sense.
2) There is the nice formula in Fourier analysis that says that the Fourier transform of f' is integral of x e^(i something), and we have a similar formula for the fractional derivative, (I think, don't quote me on that) that the Fourier transform of D^(1/2) f is integral of x^(1/2) e^(i something).
3) Fractional derivatives allow us to define nice spaces of functions (for example, those whose fractional derivatives exist and are square integrable), and sometimes in differential equations you have a solution that is not defined in the classical sense (i.e. continuously differentiable), but might belong to this nice space, which allows us to study those equations.
Ahsoka Tano This is the comment I was referring to!
Thanks Dr. Peyam!
"When Dr. Peyam teaches It's a show" believe me It is absolutely true.💜💜💜
Dr. Peyam show is very addictive.if someone enter this show,he/she never go out.
Good Gamma, what a mind blower! I need a straight jacket!
Sir you are a legend. Mind blown!!!
My PDE's professor just casually started talking about half-derivatives in undergrad and I just cried inside lmao
Hahaha
Hi ,10 ans passés que j'attends cette démonstration , en fait j'ai lu dans livre de distributions mathématiques mais sans aucune indication ,c'est magique ,les mathématiques avancent plus vite que la physique ,certainement il y aura l application de cette formule ,MERI Dr, c'est génial. write in French.
You are every bit as good as the 3b1b and bprp's of this world
❤️
Such a happy presentation. I get to go to sleep thinking about fractional calculus, thanks. : )
You just rekindled my inner math fire! ❤️😍
There is an "interesting" case where half derivative simplifies the function used as argument: Half derivative of square root of x = constant = half * (square root of pi).
Can we prove that D x = constant ? ( Or that statement is wrong ).
snnwstt It's actually a very interesting case: Yes, I think the 1/n derivative of a constant is 0, because if you apply this n times you get 0, which is the derivative of a constant. On the other hand, there's an issue because if you take the half-derivative of sqrt(x), you get a constant, and take the half derivative again, you get 0, which is not the derivative of sqrt(x) ! It's not that the definition is flawed, but just that this might not work for all functions! But any power bigger than 1/2 works!
Hum... let us note the half-derivate of something as W(something). We know that W(W(constant)) = 0 since that is the first derivate of a constant. But that does not imply that W(constant)=0. As counter example, we "could" have something along the spirit of W(a+b*i) = sqrt(a*b) + i* a ( a and b constants, i^2 = -1), so W(6) is not zero while W(W(6)) = 0. Oh, well, Cauchy-Riemann is probably applicable too so the solution I used for illustration is not really derivable, but that was just for "illustration".
That's true, you're right, we don't necessarily have W(constant) = 0, although that would certainly be a natural guess :)
Indeed, *if* Descartes' rule is applicable ( derivative of a product), then starting with the first derivative of a constant that we know to be equal to zero:
0= W(W(c))
= W(W(a*b)) since a constant c can be the product of two constants, a and b,
= W(a*W(b) + b*W(a)) by Descartes' rule
= a*W(W(b)) + W(a)*W(b) + W(b)*W(a) + b*W(W(a)) again, Descartes' rule
= 2*W(a)*W(b) since 0 = W(W(any constant))
leaving either W(a)=0, wither W(b) = 0.
Not sure that Descartes' rule is applicable, though.
snnwstt Unfortunately Descarte's rule and the quotient rule don't apply for half-derivatives, so that might not work :(
How amazingly u explained , thanku so much 😃😃
My pleasure 😊
I would love to see an animation of a plot as you let the derivative vary. I wonder if it would be a smooth animation
I didn't know Kakà is now a calculus teacher... great explanation by the way!
You kinda look like Ramanujan xD
Hahah!!! YES THATS TRUE BUT NOT FORGET THE TRUE GENIUS !!!
He does actually, now that you mention it. Haha
I have never thought about this before. Amazing!
D^(1/2) of (x)^(1/2) is just a constant? Amazing!!
Yep, it’s pretty amazing! sqrt(x) plays the role of x in the half-derivative world!
Charly Lozano I read this comment spoilers :(
wait...
Half derivative of constant is 1/2sqrt(x) ?
I had the same idea as well. But instead of x^n, I chose xe^x. The nth derivative of xe^x is (x+n)e^x which is very simple and doesn't require any analytically continued functions.
Oh wow, that’s a beautiful example, I didn’t even think about that!
Thanks I was pretty proud of it haha. I just stumbled upon this channel today and I'm loving the content so far. Keep up the great work!
Dr Peyam! WHERE HAVE YOU BEEN ALL MY LIFE???!!!
Wonderful, I really enjoyed it Dr Payam Show.
Wonderful! Your best video yet.
The donkey kong joke caught me off guard hahaha so good
Brilliant video. You just earned a sub
hey dr peyam i have never seen such thing in my maths class,although i studied calculus upto class 12. so could you please suggest me some resourses or some good books to study these stuffs of calculus
I love their energy !!!
Even before watching this, I'm gonna guess that the gamma function is involved. Taylor expansion of a function involves a factorial. You can take an nth derivative or antiderivative by taylor expanding a function. (which can be represented as just a triangular matrix operation of involving n choose k and a factorial, or just a 1/factorial diagonal matrix when x = 0). Just shift the resulting vector n terms (up for derivative, down for antiderivative), and then apply the inverse matrix. The half derivative would intuitively be a half shift of that vector would be a half shift of the factorials. So just replace the factorials with gamma(1+n) and you can shift those by any real number, or even imaginary numbers if you want to get really crazy.
There's a Fourier transform interpretation of this, too that's even more simple. Derivatives in the Fourier transform just involves multiplying the frequency domain by frequency ω^n or ω^-n for anti derivatives, so a half derivative would be
f( f(t)*ω^(1/2) )
This would do some weird shifts in the real and imaginary parts and would give you complex results for real valued functions. (the Hilbert transform might have an interesting interpretation here too, but I'm not sure what that would be)
Just realized the taylor expansion version would also give complex results since it involves raising the expansion point to a power: (-z)^-n, so that goes complex for half values.
Excellent video, thank you very much sir!
as always :) just beautiful !! thanks Dr Peyman
Dr. Peyam is a great man.
You all are enjoying yourselves. Thx. For the video.
Fantastic work,
thanks for sharing this wonderful work
great stuff and camerawork!
I'm thinking about fractional derivatives of other common functions. Here's my derivation of D^(1/2) cos(x)
1) D^(1/2) e^(ax) = sqrt(a)*e^(ax)
2) D^(1/2) e^(ix) = sqrt(i)*e^(ix) = (1 + i)/sqrt(2)*(cos(x) + i*sin(x)) = 1/sqrt(2)*cos(x) - 1/sqrt(2)*sin(x) + i*(...)
3) D^(1/2) cos(x) = real part of D^(1/2) e^(ix) = 1/sqrt(2)*(cos(x) - sin(x)) = cos(x + pi/4)
But of course it must be cos(x + pi/4), since D cos(x) = -sin(x) = cos(x + pi/2). Duh!
Martin Epstein I think that's correct, but I have to think more about this :) I'll probably make a video about half derivatives of exponential and trig functions at some point
Dr. Peyam's Show Wow, then can we solve half-differential equations like y+y*=x(y*=half-deriv of y)? :)
Yep :) Even half partial diff equations!
Thank you so much! I always asked myself if this could be possible. Very nice job
i just thought about this again and came to say: plugging in the expansion of e^x - 1, the half derivative of it is x erf(sqrt(x)) e^x + sqrt(x/pi), which is wild.
I'm rewatching this just to tell you you're awesome
Awwwwww, thanks!!!
Wish my calc 2 course covered this, neat stuff
I really love your videos, much more than before!!
Wow.... That's why I love math. And that's why I love you,Sir....
I was just wondering, does this have any application or is it just a fun thing?
This stuff is amazing! Good work guys!
Interesting ! I learned something today.
I would kill for one calc class with Dr. Peyam
Really good work 👍.
Fantastic,
But don't forget gamma function doesn't make sense when x=-1,-2,-3,...,-n,..and so on
Remember this please... so there are not connection between gamma function and n! To negative real numbers.
This is a great and natural extension of derivatives. Just like we define the 3rd operation (exponentiation) first as repeatedly multiplying ^n , then finding an inverse ^1/n and therefore having rational exponents, you apply this to the "multiplication" of differential operators.
On another note, I am always annoyed by the shift in the operand of the gamma function. I prefer having Π(n) = n!, which is much more intuitive and removes some unnecessary thinking efforts, just like with π=τ/2 (why alway 2 π, if you mean 1 period ? why always Γ(x) = x-1!).
I can't say nothing just wooooowww! I haven't seen something like this. Everything makes sense. You're awesome 😮
D^k (x^n) = n!/(n-k)! * x^(n-k) is only true if k
This was a really awesome video, but I had a couple questions. Is it mathematically rigorous to treat the derivative operators as variables when you kind of add the "exponents"/n-th order on the derivative operator? If not, what is the mathematically rigorous way to defined fractional derivatives? Also, what do fractional derivatives conceptually mean (I know what a regular derivative conceptually mean, but it's hard for me to visualize a fractional derivative)?
I've just had a Mathgasm...
Woah, I found this channel by accident. I shouldn't be surprised you're here.
So this shows that the expression given is *a* solution to "What is the half-derivative of the given expression?" But how do we know that there are not more solutions?
Man, you're so cool!! I wish i was as good as you , in maths
Great video! I was wondering if the linearity of the half derivative is ever proved, or if we just assume it?
Great video Dr., thanks
we're talking about using rational fractions... but what about irrational?
EDIT: just realized reading your pinned comment. square integration. holy crap this goes deep
FINALLY! Someone else who understands fractional derivatives! :)
Every time I mention taking fractional derivatives, I get weird looks and laughs, even from people claiming to be mathematicians with degrees ;o (I think I've seen some of them in the comments under +BlackPenRedPen videos once) So who's laughing now? :q
Sci Twi we can all go home happy now and enjoy our Xmas
Right after solving for X ;)
Sci Twi Xmas= money
X= money/mas
X= oney/as
I lost you at 1:25
Then my mind was completely boggled at 1:49
Thanks for another great video, Dr. Peyam !! How can we generalize this for any arbitrary function of x? Perhaps via the following argument? Any "reasonable" function of x can be expressed as a power series in x, within an "applicable neighborhood". Half derivative can be applied to each individual term of the expansion, and then combined back by virtue of linearity?
See playlist
Dude you're a complete nut and it's awesome!
dr peyam scares the shit out of me sometimes