Kinetics pulley example problem with a friction surface

Please support my work on Patreon: / engineer4free
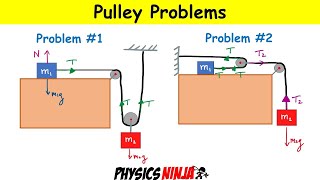
This tutorial goes over an example with a kinetic pulley and a friction surface. The general method is very similar to simple Atwood machine problems, you just have to consider the force of friction as well in the force balance of the block in contact with the surface. But otherwise, both blocks will share a common magnitude acceleration in their respective directions of travel, and the tension will also be the same acting on each block.
Links:
All Free Engineering Dynamics Tutorials (Website): www.engineer4f...
All Free Engineering Dynamics Tutorials (RUclips): • Dynamics
Dynamics Practice Problems & Solutions: www.engineer4f...
Subscribe on RUclips: / @engineer4free
Join the Mail List: www.engineer4f...
Patreon: / engineer4free
Thanks for watching, I hope it helps!

[@Abigail-gp9pf]

What the heck, why did my teacher never do it this way. IT MAKES SO MUCH MORE SENSE

[@Engineer4Free]

What the heck indeed. Glad it helps!!

[@aofddofa6661]

Uou are awesome ..5 min better than my teacher 5 hours At school

[@ItsDanielStar]

i love you, very simple and easy to comprehend

[@Engineer4Free]

Love you too

[@inhinyerongsibil6383]

very well explained and presented. Thou im now registered engineer, this topic refreshes my knowledge which is a great help to everybody

[@Engineer4Free]

Thanks so much for that feedback! Really glad to hear it 🙂

[@RandomCorner]

Awesome video man I couldn't find any explanations before I stumbled upon this

[@Engineer4Free]

Glad I could help! You should check out the full playlist here: engineer4free.com/dynamics this is video 27 out of 53 =)

[@11sayedfareen]

Thank you so much ...I was so confused as my teacher was making it complex ...

[@_H8ed_]

Wow it finally makes sense 🎉

[@justanalien7255]

It was such a savior 😭

[@Engineer4Free]

Glad I could help!! More vids here: engineer4free.com/dynamcs =)

[@elliejohnson2786]

My friend thinks of me as the smart math person, so this video was very helpful when they ambushed me with a pulley question that I hadn't done in years.

[@MATHMAN-qz3de]

question is it possible for the tow bodies to have different magnitude accelerations? like one has a 4 m/s^2 and the other -1.2m/s^2. and is there a difference to find the acceleration of the system

[@nathanwillis5607]

thanks man

[@drewchmieleski9631]

Hey Engineer4Free! I'm doing that exact problem but with different masses, but the coefficient of friction isn't given to me. How am I supposed to solve this?

[@drewchmieleski9631]

All it says is it rests against a smooth horizontal surface

[@Engineer4Free]

"smooth surface" often (but not always) refers to "frictionless." If it is indeed frictionless, then the problem basically becomes a slightly modified Atwood machine. See videos 22 - 28 here: engineer4free.com/dynamics The whole system would only be driven by the weight of the hanging block then.

[@dylanbeard9770]

Why is it w - T = ma and not T - w = ma? Wouldn't the weight be in the negative y direction?

[@manishasharma8217]

That is because in these sorts of problems, people just make the down direction positive rather than negative, since they aren’t portraying upward acceleration

[@nortezarioraveliic.1095]

I think there's something wrong; you didn't plug in the (-) sign in W-T=ma, how come T=W-ma? @3:23

[@maan_kartik]

Take the T other side and take ma this side now your eq be - w - ma = T which can also be written as T = w - ma 3:23

[@abdullahsiddiqui5830]

Hi man, I want to really ask about how make your videos. I also teach engineering statics but my lectures aren't in english. I would like some tips on how to make videos like you.

[@Engineer4Free]

Hey Abdullah, thanks for reaching out. I’ve got a full list of all the hardware and software that I use here: engineer4free.com/tools that you should check out. It’s all relatively standard stuff