
- Видео 239
- Просмотров 1 280 764
MAFarooqi
Пакистан
Добавлен 19 июн 2012
NCS - 42 - Backstepping control for strict feedback systems
This lecture extends the backstepping control technique to a more general class of nonlinear systems, called strict feedback systems. Some examples and exercise problems are presented to explain the design procedure.
Просмотров: 1 387
Видео
NCS - 35 - Chattering in Sliding Mode Control
Просмотров 1,4 тыс.10 месяцев назад
Sliding Mode Control is associated with chattering, this lecture explains the chattering phenomenon and its reasons.
NCS - 34c - Sliding Mode Control for Pendulum - Simulation Results
Просмотров 1,8 тыс.10 месяцев назад
Simulation result for the designed sliding mode control for the pendulum system are presented in this part of the lecture.
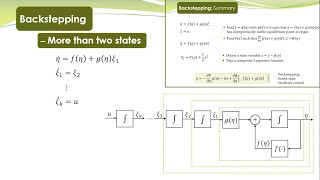
NCS - 41 - Bacstepping Control - General Case - more than two states
Просмотров 1,2 тыс.10 месяцев назад
This lecture explains the backstepping control for a more general class of nonlinear systems. Based upon the idea of simple system with only two states, the idea is extended to systems with more than two states. MATLAB/Simulink Simulations are performed to demonstrate the designed controller.
NCS - 40a - Backstepping Control - Basic Concept
Просмотров 3,5 тыс.10 месяцев назад
Basic concept of the back-stepping control for nonlinear systems is explained in this lecture. Backstepping is a very powerful technique for design of controllers for nonlinear systems. Systems with particular structure, called strict feedback systems, can be handled with this approach. This lecture explains the concept with a simple case when the system has only two states.
NCS - 40b - Backstepping Control - Example
Просмотров 2,7 тыс.10 месяцев назад
This lecture demonstrates the application of back-stepping control technique for the design of controller for nonlinear systems. MATLAB/Simulink simulations are performed to demonstrate the efficacy of the controller.
NCS - 37 - Chattering reduction in SMC (Approach 2)
Просмотров 86710 месяцев назад
This lecture demonstrates that replacing the signum function with high slope saturation function can reduce the chattering associated with sliding mode control.
NCS - 36b - Chattering reduction - MATLAB demonstration
Просмотров 86111 месяцев назад
MATLAB Simulations for demonstration of first approach for chattering reduction in sliding mode control.
NCS - 36a - Chattering Reduction (Approach 1)
Просмотров 96911 месяцев назад
Sliding Model Control (SMC) is associated with chattering phenomenon. This lecture explains an approach for reduction of chattering in SMC.
NCS - 34d - Sliding Mode Control explained with phase portraits
Просмотров 1,3 тыс.11 месяцев назад
NCS - 34d - Sliding Mode Control explained with phase portraits
NCS - 34b - Sliding Mode Control - Example of Pendulum
Просмотров 2,7 тыс.11 месяцев назад
This part of the lecture demonstrates the procedure to design sliding mode control with the help of a simple system of pendulum.
NCS - 34a - Sliding Mode Control - Basic Concept
Просмотров 10 тыс.11 месяцев назад
This lecture discusses the concept of Sliding Mode Control (SMC), which is a powerful technique for designing controllers for nonlinear systems. It explains how the control law can bring any initial condition to the sliding surface and maintain trajectories on the surface, leading to stable system dynamics. The approach is robust against uncertainties and can be implemented with a simple contro...
NCS - 19b - Examples: Invariance Set Theorem
Просмотров 898Год назад
NCS - 19b - Examples: Invariance Set Theorem
NCS - 19a - LaSalle's Invariance Set Theorem
Просмотров 1,3 тыс.Год назад
NCS - 19a - LaSalle's Invariance Set Theorem
NCS - 18b - Krasovskii's Method for Stability
Просмотров 2,4 тыс.Год назад
NCS - 18b - Krasovskii's Method for Stability
NCS - 18a - Selection of Candidate Lyapunov Function
Просмотров 2,3 тыс.Год назад
NCS - 18a - Selection of Candidate Lyapunov Function
NCS - 17b - Examples of Global Asymptotic Stability
Просмотров 1,8 тыс.Год назад
NCS - 17b - Examples of Global Asymptotic Stability
NCS - 17a - Global Asymptotic Stability - Lyapunov Theorem
Просмотров 1,9 тыс.Год назад
NCS - 17a - Global Asymptotic Stability - Lyapunov Theorem
NCS - 16b - Examples: Application of Lyapunov Stability Theorem
Просмотров 2,9 тыс.Год назад
NCS - 16b - Examples: Application of Lyapunov Stability Theorem
NCS - 16a - Lyapunov Stability Theorem, Energy Concept, Definiteness of functions
Просмотров 3,3 тыс.Год назад
NCS - 16a - Lyapunov Stability Theorem, Energy Concept, Definiteness of functions
LCS - 53c - Diagonal canonical form (DCF) representation of state equations
Просмотров 13 тыс.Год назад
LCS - 53c - Diagonal canonical form (DCF) representation of state equations
LCS - 53b - Observable Canonical Form (OCF) and signal flow graphs
Просмотров 15 тыс.Год назад
LCS - 53b - Observable Canonical Form (OCF) and signal flow graphs
LCS - 53a - Controllable Canonical Form (CCF) state-space models
Просмотров 19 тыс.Год назад
LCS - 53a - Controllable Canonical Form (CCF) state-space models
LCS - 52b - Signal flow graphs for state-space models
Просмотров 7 тыс.Год назад
LCS - 52b - Signal flow graphs for state-space models
LCS - 52a - State-space to transfer function
Просмотров 14 тыс.Год назад
LCS - 52a - State-space to transfer function
LCS - 51 - Differential equation to state-space, transfer function to state-space, block diagrams
Просмотров 6 тыс.Год назад
LCS - 51 - Differential equation to state-space, transfer function to state-space, block diagrams
NCS - 30 - Two more examples of input-output linearization
Просмотров 2,3 тыс.Год назад
NCS - 30 - Two more examples of input-output linearization
LCS - 50 - State variables and state equations
Просмотров 2,6 тыс.Год назад
LCS - 50 - State variables and state equations
NCS - 32 - Stabilization and tracking problem using feedback linearization
Просмотров 2,2 тыс.Год назад
NCS - 32 - Stabilization and tracking problem using feedback linearization
NCS - 29 - Internal dynamics, zero dynamics, and example of input-output linearization
Просмотров 3,7 тыс.Год назад
NCS - 29 - Internal dynamics, zero dynamics, and example of input-output linearization








Thank you professor. Your videos are very clear.
Good day sir, very helpful video, just quick clarification on equation 2. Shouldn't it be 3s^2+20s+1 instead of 3s^2+20s+4 since there's no spring valued at 4?
hey doc how can i find x1 x2 block in simulink ?thanku
i have known thank u for ur sharing
@mafarooqi sir apne ye chapter karwya ha ?The Design of State Variable Feedback Systems
sir i find the ans of example-1 is Theta2(s)/T(s) = 1/10 --------------------------------- 850s^2 + 2000s + 600 i think it is the right ans. can you give a suggestion?
shef please comeback ı cant finish my school without you ı need to learn power electronics please mak a video series. esselamaleykum.
God bless you my king
Thankyou Sir for this lecture...very well explained
shouldnt the error be = 1/(1+Kv) instead of 1/Kv
السلام عليكم، what is name of this tool box for simulation in matlab?
It is pplane8.m, you can run it in MATLAB.
Hi Prof. I have a question regarding the case when dE/dt == 0, that means Energy is a constant number. For pendulum, this can be the case when pendulum is in the upright position with zero velocity and acceleration. But this is not a stable equilibrium point. Then why do you say equilibrium point is table when dE/de <= 0?
A detailed answer is necessary. A system at equilibrium will remain in that state indefinitely unless disturbed externally. This applies to all equilibrium points, both stable and unstable, as indicated by dE/dt = 0 at the equilibrium point. When discussing the stability of equilibrium points, we consider the future behavior of the system's energy for trajectories that start slightly away from the equilibrium point.
@@MAFarooqi I see, this is a great explanation. Thank you so much! Btw, do you have plan to make some videos on more advanced control methods like MPC? I like your teaching style, especially for Lyapunov, you give lots of examples before dive into definitions and equations.
Thank you for the amazing video
isnt it supposed to be N2/N1?
sir i think question no. 1 K (spring) value should be 3 not 6? 300(5/50)^2 is = 3 not 6 1/10 -------------------- 8.5s+20s+3
There is a second spring as well, if you add its effect, then you will get the transfer function given in the slides.
Watch ruclips.net/video/5daCE9VBx1M/видео.html for MATLAB Simulation/Animation of an Inverted Pendulum with LQR (Linear Quadratic Regulator).
thank u sho much sir
Thank you, sir.
sb koi alg alg bta rha h dimag khra b h
Thank you sir, for the detailed, descritive video❤
Thank you sir❤
Jazakallah brother, really good explanation
Sir,could u pls send me these pdf files?(I am a student in Beihang university,China,found ur videos r very helpful.)
drive.google.com/drive/folders/1KlLqvsKJ8VALBHYEs3HZB_UuYcSvGJs2
great video sir
Dear Professor Thank you for your lecture. Why we should consider P is symmetry matrix.
Candidate Laypunov function must be positive definite. For linear systems, x'Px can be taken as a Lyapunov function, with P a positive definite matrix. Remember that positive definiteness is only defined for symmetric matrices.
Dear Professor Many thanks for your time and support on my doubts.
Dear Professor Thank you for your wonderful explanation about Lyapunov function.
Can you give a link to the related books you are using? Also thanks for the amazing content. May Allah give you an infinite reward for the good work.
A useful reference is the book Nonlinear Systems by Hassan Khalil.
Hey I just want to say, I used some of these videos for my course magnetic circuits last year.... this year I have a course called Electric Machines! And its based on the same previous stuff we learnt plus some new stuff. Which by coincidence is the name of this exact playlist of videos made by you! Thank you and have a great day
Thank you so much for this video it is very clear explanation. Could you please make a video about controllability canonical form and observability canonical form ? ( I couldn't find any video or material about this topic but our professor includes these topics to the lecture)
Controllable ( or Controllability ) canonical form ruclips.net/video/sYguf97Rnjk/видео.html
You teach much better compared to my teacher HAHAHAHAH
Sir thank you for sharing us good and comprehensive videos...also can you share us the topics about AC motors also
Make a playlist also about AC motors... you teach much better compared to my teacher ahhahahaha😅
Ba monk bapa UNZA leave a like 🇿🇲😹 Machines teyabana ... this man deserves to be dean
يسعدلي جوك ياشيخ
So helpful, could you please share the slides?
drive.google.com/drive/folders/1KlLqvsKJ8VALBHYEs3HZB_UuYcSvGJs2
@@MAFarooqi thank you
I want to know if the data used for the calculation are per-phase data
Why is there no equivalent circuit of the permanent magnet?
Thank you so much sir! My professor does not draw much that is why his lecture is really hard to understand when it comes to looking at different perspectives of the machine 😭
If you are here because of Dr. Zulu leave a like UNZA monk
Yayaya 😂😂😂😅
@@hichuunduhabeenzu3574 let's hope siza menya peka peka quiz yaba Mudala. 😹😹
Yeah😂
😂😂😂
niyokaba🤣🤣🤣🤣
5:51 in and i feel ready for my assignment. My uni lecturer failed to explain the steps in over an hour
AoA, Can you please upload your lectures on Robust Control?
Sir,, Please do not share this type of vedio which are wrong. Please , please
dear sir , what is a b c and d
These are commutator segments. Now, what are commutator segment? This is elaborated in Lecture 15.
@@MAFarooqi_sir, Thank you sir
farooqi saab,masha allah kya gazab ke lectures banaya hai aapne
hello. firstly, thank you for your video it is helpful to me i'm curious about why gain is 164 i will get happy if you answer to me
Explained in lecture 35 at the following link ruclips.net/video/Jp06lFFvxWc/видео.htmlsi=PX8LznTK2v9Oza06
@@MAFarooqi Thanks so much
👍
Great video! Thanks for sharing your explanation!
Thank you Sir for your videos but 5:30 to 7:00 is confusing me .
The flux density in the air gap is not only function of angular position but also function of time.
Good explanation! But I really didn't understand the definition of V(x). Can we choose it arbitrarily?
Any positive definite function can be taken as V(x). Further guidelines for selection of V(x) is in the lecture at ruclips.net/video/-BhjiV6WP3s/видео.html
@@MAFarooqi Thanks! really appreciate your explanation😄
Hello! Professor, Thank you for your lectures. I have one doubt. If we use some hyperbolic function like tanh(ks) where k is a larger number so that function approaches sgn(s). can we use this type of function? so that my control action will become, u = -\beta(x) * tanh(k*s).
Thank you Professor!
Thank you so much sir!