
- Видео 760
- Просмотров 708 403
ILIEKMATHPHYSICS
США
Добавлен 12 мар 2014
Hello! I like to make videos on mathematical proofs and derivations!
Geometric Explanation of arctan x = lim(2^n xn) = lim(2^n xn / sqrt(1+xn^2)) (ILIEKMATHPHYSICS)
This video is part of the “Real Analysis” series I am making.
Thanks and enjoy the video!
Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS
Note that this video is not a proof that the sequences converge to arctan x. The purpose here is to give a geometric perspective of what the two sequences look like.
Proof that 2^n xn converges video: ruclips.net/video/41mHRdnpp7o/видео.html
Proof that 2^n xn / sqrt(1+xn^2) converges video: ruclips.net/video/seEyryvLOJk/видео.html
Thanks and enjoy the video!
Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS
Note that this video is not a proof that the sequences converge to arctan x. The purpose here is to give a geometric perspective of what the two sequences look like.
Proof that 2^n xn converges video: ruclips.net/video/41mHRdnpp7o/видео.html
Proof that 2^n xn / sqrt(1+xn^2) converges video: ruclips.net/video/seEyryvLOJk/видео.html
Просмотров: 652
Видео
An Alternative Definition of ln(x): the limit of 2^n(xn - 1) and 2^n(1 - 1/xn) (ILIEKMATHPHYSICS)
Просмотров 5084 часа назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Proof of limit of n(x^1/n - 1) = ln(x) video: ruclips.net/video/96z-uCrq7LA/видео.html Link to Hurwitz's paper: ia600708.us.archive.org/view_archive.php?archive=/28/items/crossref-pre-1923-scholarly-works/10.1007%2Fbf01449600.zip&file...
Prove that lim n(x^1/n - 1) = ln(x) (ILIEKMATHPHYSICS)
Просмотров 3,1 тыс.7 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS
Prove if x ﹥ 0, then lim(x^1/n) = 1 (Second Proof) (ILIEKMATHPHYSICS)
Просмотров 8679 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS
Prove if x ﹥ 0, then lim(x^1/n) = 1 (First Proof) (ILIEKMATHPHYSICS)
Просмотров 3969 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that the exponential function is continuous video: ruclips.net/video/OYFCBE-aFJg/видео.html
Prove the limit of sin(x) / x = 1 as x approaches 0 (ILIEKMATHPHYSICS)
Просмотров 1,7 тыс.12 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that 2^n xn converges (definition of arctan) video: ruclips.net/video/41mHRdnpp7o/видео.html Prove if x ﹥ 0, then x/sqrt(1 x^2) ﹤ arctan(x) video: ruclips.net/video/seEyryvLOJk/видео.html Prove that |arctan x| = arctan|x| video ...
Prove that sin(x) / cos(x) = tan(x) (ILIEKMATHPHYSICS)
Просмотров 1,6 тыс.14 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that e^z * e^w = e^(z w) video: ruclips.net/video/PK0JxSVo7oE/видео.html Proof that 2^n xn converges (definition of arctan) video: ruclips.net/video/41mHRdnpp7o/видео.html Prove that arctan is bounded (definition of pi) video: r...
Prove that cos(x) is decreasing on [0,π] (ILIEKMATHPHYSICS)
Просмотров 59314 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that sin2x - sin2y = 2sin(x-y)cos(x y) and cos2x - cos2y = -2sin(x-y)sin(x y) video: ruclips.net/video/XZh2EGS7Xxg/видео.html Prove that cos(x) ﹥ 0 for all x in -π/2 ﹤ x ﹤ π/2 video: ruclips.net/video/wXIwDQSwTHc/видео.html Last...
Prove that cos(x) ﹥ 0 for all x in -π/2 ﹤ x ﹤ π/2 (ILIEKMATHPHYSICS)
Просмотров 63116 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that 2^n xn converges (definition of arctan) video: ruclips.net/video/41mHRdnpp7o/видео.html Prove that arctan : R → (-π/2, π/2) is onto video: ruclips.net/video/A45bHcz1zH4/видео.html Prove that arctan(1) = π/4 video: ruclips.n...
What is sin(nπ/2) = ? and cos(nπ/2) = ? (ILIEKMATHPHYSICS)
Просмотров 28716 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Video containing proof of cos(π/2) = 0 and sin(π/2) = 1: ruclips.net/video/bKa8yU5L-KA/видео.html Proof of De Moivre's Theorem video: ruclips.net/video/7nKKfWLdvnI/видео.html
Prove De Moivre's Theorem (cosz + isinz)^k = coskz + isinkz (ILIEKMATHPHYSICS)
Просмотров 1 тыс.19 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Proof that cosine is even and sine is odd video: ruclips.net/video/Zea-Yf3FVbk/видео.html Prove the sine and cosine addition formulas video: ruclips.net/video/tOAmJkv3YWE/видео.html Prove that sin^2(z) cos^2(z) = 1 video: ruclips.net/...
Prove that sin(x) and cos(x) are continuous (ILIEKMATHPHYSICS)
Просмотров 1,1 тыс.19 часов назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that |sin(x)| ≤ 1 and |cos(x)| ≤ 1 video: ruclips.net/video/9lpPcf-ic6M/видео.html Prove that |sin(x)| ≤ |x| video: ruclips.net/video/UeQqg17pDHU/видео.html Prove that sin2x - sin2y = 2sin(x-y)cos(x y) and cos2x - cos2y = -2sin(...
Prove that sin2x - sin2y = 2sin(x-y)cos(x+y) and cos2x - cos2y = -2sin(x-y)sin(x+y)
Просмотров 18321 час назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Proof that cosine is even and sine is odd video: ruclips.net/video/Zea-Yf3FVbk/видео.html Prove the sine and cosine addition formulas video: ruclips.net/video/tOAmJkv3YWE/видео.html
Prove that |sin x| ≤ |x| (ILIEKMATHPHYSICS)
Просмотров 2,2 тыс.21 час назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that 2^n xn converges (definition of arctan) video: ruclips.net/video/41mHRdnpp7o/видео.html Prove if x ﹥ 0, then x/sqrt(1 x^2) ﹤ arctan(x) video: ruclips.net/video/seEyryvLOJk/видео.html Prove that |arctan x| = arctan|x| video ...
Prove that cos(2arctanx) = 1-x^2 / 1+x^2 and sin(2arctanx) = 2x / 1+x^2 (ILIEKMATHPHYSICS)
Просмотров 309День назад
This video is part of the “Real Analysis” series I am making. Thanks and enjoy the video! Real Analysis Playlist: ruclips.net/p/PLDiddIbnOEOWLbdQ4DoC8bfaV_y4VyOsS Prove that 2^n xn converges (definition of arctan) video: ruclips.net/video/41mHRdnpp7o/видео.html Prove that e^2iarctanx = 1 ix / 1-ix video: ruclips.net/video/9vzCYkw_oFs/видео.html Prove that cos(x) = Re(e^ix) and sin(x) = Im(e^ix)...
Prove that |sin x| ≤ 1 and |cos x| ≤ 1 (ILIEKMATHPHYSICS)
Просмотров 1,5 тыс.День назад
Prove that |sin x| ≤ 1 and |cos x| ≤ 1 (ILIEKMATHPHYSICS)
Prove that sin^2(z) + cos^2(z) = 1 (ILIEKMATHPHYSICS)
Просмотров 319День назад
Prove that sin^2(z) cos^2(z) = 1 (ILIEKMATHPHYSICS)
Prove the sine and cosine addition formulas for complex numbers (ILIEKMATHPHYSICS)
Просмотров 395День назад
Prove the sine and cosine addition formulas for complex numbers (ILIEKMATHPHYSICS)
Prove that cos(-z) = cos(z) and sin(-z) = -sin(z) (ILIEKMATHPHYSICS) (cos is even and sine is odd)
Просмотров 673День назад
Prove that cos(-z) = cos(z) and sin(-z) = -sin(z) (ILIEKMATHPHYSICS) (cos is even and sine is odd)
Prove Euler's Formula e^iz = cos(z) + isin(z) (ILIEKMATHPHYSICS)
Просмотров 569День назад
Prove Euler's Formula e^iz = cos(z) isin(z) (ILIEKMATHPHYSICS)
Prove that cos(x) = Re(e^ix) and sin(x) = Im(e^ix) (ILIEKMATHPHYSICS)
Просмотров 461День назад
Prove that cos(x) = Re(e^ix) and sin(x) = Im(e^ix) (ILIEKMATHPHYSICS)
Prove that the conjugate of e^z is equal to e^conjugate of z (ILIEKMATHPHYSICS)
Просмотров 493День назад
Prove that the conjugate of e^z is equal to e^conjugate of z (ILIEKMATHPHYSICS)
Prove if zn converges to z, then zn conjugate converges to z conjugate (ILIEKMATHPHYSICS)
Просмотров 19814 дней назад
Prove if zn converges to z, then zn conjugate converges to z conjugate (ILIEKMATHPHYSICS)
Prove that arctan(1) = π/4 (ILIEKMATHPHYSICS) (Real Analysis)
Просмотров 92014 дней назад
Prove that arctan(1) = π/4 (ILIEKMATHPHYSICS) (Real Analysis)
Prove that arctan : R → (-π/2, π/2) is onto (ILIEKMATHPHYSICS) (definition of tan(x))
Просмотров 33314 дней назад
Prove that arctan : R → (-π/2, π/2) is onto (ILIEKMATHPHYSICS) (definition of tan(x))
Prove that lim{x→∞} arctan(x) = π/2 and lim{x→-∞} arctan(x) = -π/2 (ILIEKMATHPHYSICS)
Просмотров 41514 дней назад
Prove that lim{x→∞} arctan(x) = π/2 and lim{x→-∞} arctan(x) = -π/2 (ILIEKMATHPHYSICS)
Prove that arctan(x) is bounded (ILIEKMATHPHYSICS) (includes a definition of pi)
Просмотров 34814 дней назад
Prove that arctan(x) is bounded (ILIEKMATHPHYSICS) (includes a definition of pi)
Prove that arctan(x) is continuous (ILIEKMATHPHYSICS)
Просмотров 48714 дней назад
Prove that arctan(x) is continuous (ILIEKMATHPHYSICS)
arctan(x) is an increasing function (Proof) (ILIEKMATHPHYSICS)
Просмотров 49614 дней назад
arctan(x) is an increasing function (Proof) (ILIEKMATHPHYSICS)
If xy ﹤ 1, then arctan(x) + arctan(y) = arctan((x+y)/(1-xy)) (Proof) (ILIEKMATHPHYSICS)
Просмотров 37114 дней назад
If xy ﹤ 1, then arctan(x) arctan(y) = arctan((x y)/(1-xy)) (Proof) (ILIEKMATHPHYSICS)





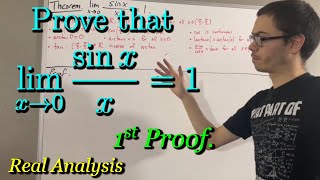
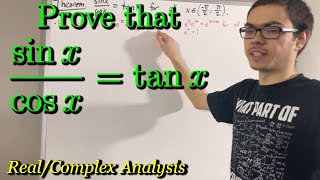
![Prove that cos(x) is decreasing on [0,π] (ILIEKMATHPHYSICS)](http://i.ytimg.com/vi/B2-7ej8bdcI/mqdefault.jpg)
