- Видео 9
- Просмотров 287 669
jHan
США
Добавлен 10 янв 2021
Mathematics can sometimes be frustrating and unintuitive. This channel seeks to explain and express mathematical concepts and ideas in a beautiful, intuitive way. Animations are made with 3Blue1Brown's animation engine Manim: github.com/3b1b/manim
The Axiom of Choice
Mathematics is based on a foundation of axioms, or assumptions. One of the most important and widely-used set of axioms is called Zermelo-Fraenkel set theory with the Axiom of Choice, or ZFC. These axioms define what a set is, which are fundamental objects in mathematics. And the Axiom of Choice is arguably one of the most important and interesting axioms of ZFC. But what does it really say? And how is it used? This video dives deep into the formal definition of the Axiom of Choice, as well as its important equivalences which have their own fascinating applications in various branches of mathematics. Furthermore, we look into the controversy behind AC, and why it has garnered much discuss...
Просмотров: 79 491
Видео
Genius Mathematicians Lost Too Soon
Просмотров 2,8 тыс.10 месяцев назад
Some mathematicians changed the field of mathematics at a young age, only to die too early. Let us look at the lives of some of these young, brilliant minds who left too soon. Evariste Galois was a French mathematician who laid the foundations of abstract algebra and Galois theory, proving the quintic's insolubility. Srinivasa Ramanujan was an Indian mathematician who, upon his genius being dis...
But what is a Vector Space?
Просмотров 3,1 тыс.11 месяцев назад
Vectors are fundamental tools in mathematics and sciences. Yet different fields like mathematics, physics, and engineering seem to define vectors differently. It is mathematics, unsurprisingly, that formally defines a vector. We will go through this process of formalization, using the foundational tools of abstract algebra to define and construct a vector space. Additional Resources: Wikipedia ...
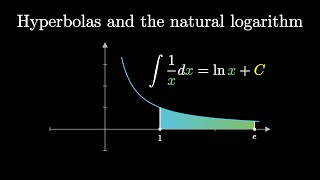
Why Logarithms Appear in This Integral
Просмотров 2,2 тыс.Год назад
Before the days of Calculus, one Pierre de Fermat wanted to find the area under the function f(x)=x^n. This problem we now call "integration" was then called "quadrature" or "squaring". Fermat was able to square every function f(x)=x^n for any rational n except for one case: n=-1 (that is, the hyperbola). It turns out that this unique nature of the hyperbola was tied to logarithms and Euler's n...
How to Find the Biggest Primes
Просмотров 8 тыс.Год назад
How do people find big primes? These primes have millions of digits, and may take years of collective effort and computing power to be found. Unsurprisingly, mathematicians have figured out various ways to more efficiently and accurately find these big primes. In the process, the unique and interesting properties of various primes have also been found. Great Internet Mersenne Prime Search: www....
Cardinality of the Continuum
Просмотров 53 тыс.Год назад
What is infinity? Can there be different sizes of infinity? Surprisingly, the answer is yes. In fact, there are many different ways to make bigger infinite sets. In this video, a few different sets of infinities will be explored, including their surprising differences and even more surprising similarities. 0:00 - Euclid's Proof of Infinite Primes 1:55 - Bigger Infinities? 2:27 - Set Theory and ...
The Cardinality of an Interval
Просмотров 2,7 тыс.2 года назад
Cantor's Diagonal Argument proves that there are an uncountable number of real numbers. But what about any interval of real numbers? Are those sets uncountable as well, no matter how small the interval?
Can the power of two irrationals be rational?
Просмотров 4,1 тыс.2 года назад
Are there two irrational numbers, let’s say x and y, such that x to the y is rational? The answer to this question brings us through a fascinating journey about transcendental numbers and the Gelfond-Schneider theorem. Additional Resources: Where I found this theorem: math.stackexchange.com/questions/728223/simple-beautiful-math-proof/728276 Music: www.purple-planet.com Animations were made by ...
Why do trig functions appear in Euler's formula?
Просмотров 132 тыс.2 года назад
Why do trig functions appear in Euler’s formula? This was the question I had when I first saw Euler’s formula. This connection between trigonometry and exponents seems so unexpected, especially along with complex numbers. To answer this question, we must journey into the intricate and beautiful mathematical relationship between trig functions, e, and complex numbers. We will look at two differe...