A Nice Radical Equation With Parameters

🤩 Hello everyone, I'm very excited to bring you a new channel (SyberMath Shorts).
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
/ @sybermath
/ @aplusbi
⭐ Join this channel to get access to perks:→ bit.ly/3cBgfR1
My merch → teespring.com/...
Follow me → / sybermath
Subscribe → www.youtube.co...
⭐ Suggest → forms.gle/A5bG...
If you need to post a picture of your solution or idea:
in...
#algebra #counting #geometry #numbertheory #calculus
via @RUclips @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
▶ Trigonometry: • Trigonometry
▶ Algebra: • Algebra
▶ Complex Numbers: • Complex Numbers
▶ Calculus: • Calculus
▶ Geometry: • Geometry
▶ Sequences And Series: • Sequences And Series

[@mikeyu3243]

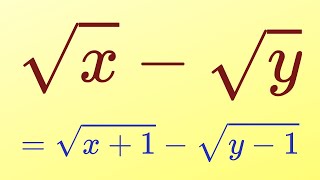
Inversed: 1/(sqrt(x+a)+sqrt(x)) = 1/a
multiply sqrt(x+a)-sqrt(x) to left, the result is 1

[@icfj77]

this problen has sense only for a=0, and a>1, a=1.

[@chaosredefined3834]

Method 4. In other words, how I'd do it if I didn't spot the diff of squares.
sqrt(x + a) + sqrt(x) = a
sqrt(x + a) - sqrt(x) = b
Subtract the two:
2 sqrt(x) = a - b
Divide through by 2
sqrt(x) = (a - b)/2
Square it
x = (a^2 - 2ab + b^2)/4
Add the initial two:
2 sqrt(x + a) = a + b
Divide through by 2
sqrt(x + a) = (a + b)/2
Square it
x + a = (a^2 + 2ab + b^2)/4
Substituting in the x from the subtraction step:
(a^2 - 2ab + b^2)/4 + a = (a^2 + 2ab + b^2)/4
Multiplying through by 4
a^2 - 2ab + b^2 + 4a = a^2 + 2ab + b^2
Subtract a^2 + b^2 from both sides
-2ab + 4a = 2ab
Add 2ab to both sides
4a = 4ab
Either a = 0 or b = 1.
Well, we wanted b. So, b = 1, unless a = 0. Let's check that cases:
sqrt(x + 0) + sqrt(0) = 0
sqrt(x) = 0
x = 0
sqrt(0 + 0) - sqrt(0) = 0 - 0 = 0.
So, if a = 0, then b = 0. Otherwise, b = 1.

[@ProactiveYellow]

Given the first equation, we have
√(x+a)+√x=a
Add and subtract x on the right
√(x+a)+√x=x+a-x
We can factor a difference of squares on the right
√(x+a)+√x=(√(x+a)+√x)(√(x+a)-√x)
Notice that the LHS and RHS have the same expression multiplied by our target expression. This only works in two cases:
1. The LHS expression is 0. If this is the case, then √(x+a)+√x=0=a →2√x=0→x=0, so √(x+a)-√x=√(0+0)-√0=0
2. The target expression is the multiplicative identity, that is, √(x+a)-√x=1
These are the only two solutions.

[@surenderkumar4560]

Rationalize the numerator and the answer in the 2nd step is 1

[@paulortega5317]

Method 3 please. LOL

[@yakupbuyankara5903]

1

[@Kraken-lm1cx]

I just multiplied sqrt(x + a) + sqrt(x) = a by sqrt(x + a) - sqrt(x) on both sides to get:
a = a(sqrt(x + a) - sqrt(x) )
Clearly if a != 0, sqrt(x + a) - sqrt(x) = 1

[@Uranyus36]

simple:
for a =/= 0,
(sqrt(x+a) + sqrt(x))(sqrt(x+a) - sqrt(x)) = x + a - x
a(sqrt(x+a) - sqrt(x)) = a
(sqrt(x+a) - sqrt(x)) = 1
for a = 0, x = 0 so (sqrt(x+a) - sqrt(x)) = 0

[@jacobcohen2957]

The solution is valid for a>1.
Otherwise, sqrt(x) = (a-1)/2 is negative.

[@maxgoldman8903]

Do we need to consider the absolute value for √ (·)² appearing in method 1 and 2 when there’s no specification on parameter a?

[@omni-e1w]

Absolutely.

[@yurenchu]

Answer:
√(x+a) - √x = 1 OR √(x+a) - √x = 0
Calculation:
√(x+a) + √x = a
√(x+a) - √x = ?
(√(x+a) + √x) * (√(x+a) - √x) =
= (√(x+a))² - (√x)²
= (x+a) - x
= a
==>
(√(x+a) + √x) * (√(x+a) - √x) = a
and
(√(x+a) + √x) = a
==>
a * (√(x+a) - √x) = a
a * (√(x+a) - √x) - a = 0
a * [ (√(x+a) - √x) - 1 ] = 0
[ (√(x+a) - √x) - 1 ] = 0 OR a = 0
(√(x+a) - √x) = 1 OR a = 0
(√(x+a) - √x) = 1 OR (√(x+a) - √x) = (√(x+0) - √x) = (√x - √x) = 0

[@xgx899]

From (A-B)(A+B)=A^2-B^2, first expression times the second = a. Hence the second is 1. Another presentation by cybermath that is long-winded and trivial.