Integral of x/(2x - 1)
HTML-код
- Опубликовано: 8 фев 2025
- Integral of x/(2x - 1)
If you enjoyed this video please consider liking, sharing, and subscribing.
Udemy Courses Via My Website: mathsorcerer.com
Free Homework Help : mathsorcererfo...
My FaceBook Page: / themathsorcerer
There are several ways that you can help support my channel:)
Consider becoming a member of the channel: / @themathsorcerer
My GoFundMe Page: www.gofundme.c...
My Patreon Page: / themathsorcerer
Donate via PayPal: paypal.com/don...
***********Udemy Courses(Please Use These Links If You Sign Up!)************
Abstract Algebra Course
www.udemy.com/...
Advanced Calculus Course
www.udemy.com/...
Calculus 1 Course
www.udemy.com/...
Calculus 2 Course
www.udemy.com/...
Calculus 3 Course
www.udemy.com/...
Calculus 1 Lectures with Assignments and a Final Exam
www.udemy.com/...
Calculus Integration Insanity
www.udemy.com/...
Differential Equations Course
www.udemy.com/...
Differential Equations Lectures Course (Includes Assignments + Final Exam)
www.udemy.com/...
College Algebra Course
www.udemy.com/...
How to Write Proofs with Sets Course
www.udemy.com/...
How to Write Proofs with Functions Course
www.udemy.com/...
Trigonometry 1 Course
www.udemy.com/...
Trigonometry 2 Course
www.udemy.com/...
Statistics with StatCrunch Course
www.udemy.com/...
Math Graduate Programs, Applying, Advice, Motivation
www.udemy.com/...
Daily Devotionals for Motivation with The Math Sorcerer
www.udemy.com/...
Thank you:)
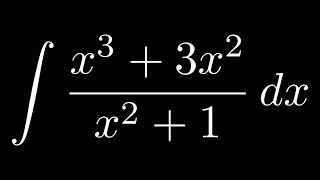








How to the integration of
2x/1+x dx
Please solve
Gotta love shortcuts! 😁
Thanks got it❤
Thank you!!!
Very unique integration 👌
I did it bt subbing 2x-1 = t, differentiating it, then solving for x in terms of t and finally putting all the numbers into the integral. It's longer than your method and slightly more tedious. So I loved your shortcut!
Is there a extra -1/4 left in your style?
@@mr.ravager.1306 No, the my final answer matches his answer
@@mr.ravager.1306 it doesn't really matter if there is a -1/4 since its a constant but if you solve this using t = 2x-1 you will get a -1/4
Thnx sr
a question about integrals: when using substitution can you solve for x and do dx=f'(u)du ? with f(u)= solution of x
Thanks Sir. Useful video.
integral of (e^2x+2e^x-e^-x-1)*e^(e^x+e^-x) dx= g(x)*e^(e^x+e^-x)+c where c is the constant of integration then g(0)+?
❤❤❤❤
Bro in India we do these sums without using a pen 😂
Why didn't you just equate the denominator to 'u' directly ?
Finally
I think the answer is wrong
The correct answer is
0.5x-0.25+0.25ln|2x-1|+c
But your method is correct it show me how to solve such these problems.
Khoya 3lash derti changement de variable
To a layperson, this is a bit hard to follow. Is it possible to explain the steps just a little bit more?
You want the integral to be in a form where you can use u-substitution. Problem is, there's an x term in the numerator which prevents you from using substitution.
So the first step is to make it so that there are like terms in both the numerator and denominator. Do this by multiplying the numerator by 2. Because you essentially add a 2 from "nowhere", you also have to multiply it by 1/2 so it cancels out. You can pull the 1/2 constant outside the integral. To match the denominator, add a '-1' as well. But again, you can't just add '-1' from nowhere so add a '+1' to cancel it out.
Then separate the fraction by representing it as (2x - 1)/(2x - 1) + (1 / (2x - 1)). (2x - 1) /(2x - 1) equals 1. Integration rule for addition states that you can represent an integral of the addition of two functions as two separate integrals of each function adding each other. You also have to distribute the 1/2 constant across both integrals. The problem then becomes 1/2 ∫ 1 dx + 1/2 ∫ 1/(2x - 1) dx. The antiderivative of '1' is just x + c. It's basically the Power Rule, 1 = x^0 so the antiderivative is x^1 / 1 = x + c. You don't have to write the + c due to redundancy, but it's a good reminder that antiderivatives/indefinite integrals always have the '+ c' constant of integration in answer.
For the second integral, you can use u-substitution. Let u = 2x - 1. Differentiating both sides gets du/dx = 2. Or just simplify it by writing du = 2 dx. Divide both sides by 2 and you get (1/2)du = dx. Rewrite the integral in terms of u. So the integral is 1/2(1/2) ∫ 1/u du. Antiderivative of '1/u' is ln|u| + c. Substitute back in terms of x so it becomes ln|2x - 1| + c. Final answer is (1/2)x + (1/4)ln|2x - 1| + c.
Hope this helped!
@@JasonJia11 Thanks, very much appreciated! Will have to review.
there should be a -1/4
Why?
@@marcushendriksen8415 actually it doesn't really matter if there is a -1/4 since its a constant but if you solve this using u = 2x-1 you will get a -1/4
@@Crackkka
No. Solution is true.