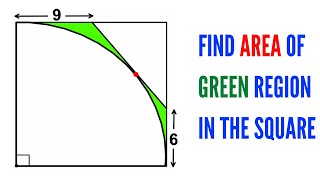
Can you find the area of the Green shaded region? | (Quarter circle in a square) |
HTML-код
- Опубликовано: 3 фев 2025
- Learn how to find the area of the Green shaded region. Quarter circle is inscribed in a square. Important Geometry and Algebra skills are also explained: area of a triangle formula; area of a sector formula; Pythagorean theorem. Step-by-step tutorial by PreMath.com
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!
Step-by-step tutorial by PreMath.com
• Can you find the area ...
Need help with solving this Math Olympiad Question? You're in the right place!
I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at
/ premath
Can you find the area of the Green shaded region? | (Quarter circle in a square) | #math #maths
Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!
#FindGreenArea #Square #QuarterCircle #AreaOfSector #SOHCAHTOA #Radius #AreaOfTriangle #CircleTheorem #GeometryMath #EquilateralTriangle #PythagoreanTheorem #PerpendicularBisectorTheorem
#MathOlympiad #ThalesTheorem #RightTriangle #RightTriangles #CongruentTriangles
#PreMath #PreMath.com #MathOlympics #HowToThinkOutsideTheBox #ThinkOutsideTheBox #HowToThinkOutsideTheBox? #FillInTheBoxes #GeometryMath #Geometry #RightTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam
How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the Radius
Equilateral Triangle
Pythagorean Theorem
Area of a circle
Area of the sector
Right triangles
Radius
Circle
Quarter circle
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun
Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.








Nice problem! Thanks!
Happy to help!
Thanks a lot ❤️🌹
Excellent exercise
Your geometry skills are superb , and so are your detailed solutions .
Glad you like them!
Thanks a lot ❤️🌹
That was just too clean explain for the problem 👏👏👏
Excellent and awesome! Nice question and great explanation. Thanks a million!👍👏
Glad you liked it! ❤️🌹
Angle PBC = 15 degrees.
Area of triangle PBC = 0.5 x 2 x root 2 x sin 15 degrees.
Root 2 x sin 15.
Triangle QBC same area, therefore sum of both = 2 x root 2 x sin 15.
Root 8 x sin 15 = 0.732.
Area of 30 degree sector = Pi x 4 /12 = Pi /3 = 1.0472.
Green area = 1.0472 - 0.732 = 0.315.
I was so stumped when I saw the thumbnail - as soon as you drew the lines to the radius it all clicked! What a clever puzzle to solve, thank you for sharing it!
The area of 1/4 Circle that includes green area is 1/4(2X2 )X 3.14.units = 3.14 units and there are three 1 by 1 squares, which is 3 square unis altogether. Therefore, 3.14units minus three units are approximately 0,14 units.
After establishing the sector PQ subtends angle 30. We calculate PQ from which we infer that PC=CQ=sqrt(3)-1. Then, the result follows as ( sector PBQ - triangle BPQ + triangle PQC) area=pi/3-sqrt(3)+1.
Very good
Thanks ❤️
A very interesting problem. Enjoyed watching for the solution, I didn't get but I will now try it out myself as an exercise. Thank you teacher!☀
Thanks my dear friend ❤️🌹
Thanks Professor. You the Best😊
You rock! ❤️🌹
By observation (the picture makes me think of the unit circle), we can see the BPG is an equilateral triangle so PD= sqrt3, so PC=sqrt3-1 and the sum of the area of the 2 congruent triangles BCP and BCQ = sqrt3-1
Area of the green region= Area of the 30 degree sector - area of the sum of BCP and BCQ = pi x 4 /12 - (sqrt3-1)= pi/3 - sqrt3+1
sin α = ½R / R = 1/2
α = 30°
Side of green region
(s +1) = R cos α = 2.√3/2
s = 0,73205 cm = √3-1
Area of angular sector:
A= ½αR² = ½.30°.2²
A = 1,0472 cm² = π/3
Area of 2 triangles:
A = 2 . (½ b.h)
A = s. R/2 = (√3-1).1
A = 0,73205 cm² = √3-1
Area of green region:
A = A₁ - A₂
A = 1,0472 - 0,73205
A = 0,31515 cm² ( Solved √ )
Nice solution sir 🎉🎉
First comment
Thanks dear ❤️
asnwer=1 cm isit 1
Before viewing: a quick very rough estimate to ensure my final answer is in the correct ballpark. It looks about 1/3 sq un or about (1/10)pi, sq un, depending on the final formatting.
Quadrant radius is 2, so quadrant area is (4 pi)/4 = pi sq un. BC = sqrt(2) and C to the quadrant’s closest circumference is 2 - sqrt(2). Take C as a new circle centre with radius of 2 - sqrt(2). Green area is ((2 - sqrt(2))^2 * pi
((2 - sqrt(2))^2 = 4 - 4*sqrt(2) + 2. Simplify to 6 - 4*sqrt(2), then multiply by pi.
I'm getting 1.078... which is clearly wrong.
Aha. It's a smaller quadrant. I forgot to divide by 4. Oops! It's 0.2695... A bit less than my visual, very rough estimate, but close enough for me to go with it.
Thanks ❤️
I went wrong with this one but, more importantly, I now see where and why. It might have been a good idea if I'd realised sooner that C cannot be the circle centre of the smaller quadrant. Ho-hum. I move on :)
Alternatively, let M and N be the midpoint of AH and HG, it's easy to calculate the area of AHG, AMP. AMP=QNG, so MPQNH=AHG-2*AMP, PCQ=MCNH - MPQNH
How do you calculate the area of AMP ?!
After we find that the sector PBQ is 30 degree, then we can conclude that its area is one third of the sector ABQ which area is pi. The total areas of PBC and QBC = sq root 3 -1, therefore the green area is pi - (sq root 3 -1) = pi - 3 + 1.
Good afternoon....how can drive the relation which make me find the third line of non-right angle triangle.I have the value of the other tow lines and the angle between there.
Please sir....not the low.....
I want driving the low.
Thank you very much
شكرا
يمكن استعمال حساب التكامل......
Thanks ❤️
Nice 👍❤
Thanks ✌
π = area of 1/4 circle; π/3 + √3/2 = area in 1/4 circle above center, and the same area in 1/4 circle to the right of center. Thus, 2(π/3 + √3/2) - 1 = area in 1/4 circle excluding green area, and green area is π - [(2π/3 + √3) - 1] = 0.31515...
👍
Thanks ❤️
Draw BP, BG, and BC. Let M be the midpoint of BG and N be the midpoint of BA. As BP and BG are radii of the quarter circle, BP = BG = 2. As BP = 2 and BM = 1, ∆PMB is a 30-60-90 special right triangle, and PM = √3. By symmetry, QN is also √3. By observation, PC and QC are √3-1.
Triangle ∆CBP:
A = bh/2 = (√3-1)1/2 = (√3-1)/2
By symmetry, ∆CBQ = (√3-1)/2 as well, so quadrilateral CPBQ = √3-1.
As ∠PBM = 60°, ∠ABP = ∠GBQ = 30°, so ∠PBQ = 90-30-30 = 30°.
Sector PBQ:
A = (θ/360)πr² = (30/360)π2² = 4π/12 = π/3
Green area:
A = Sector PBQ - CPBQ
A = π/3 - (√3-1) = 1 + π/3 - √3 ≈ 0.315
Basis triangle BEP the side BE is sqrt3
Now sides AB and GH are parallel with right angles and sides equal making it square
Thus, at the centre of square .the intersection will be at right angles meaning green part is quarter circle
Since mid pointscare connecting
Further side CP can now be deduced as sqrt3 -1
Therefore area of green section is pi * (sqrt3 -1)^2 /4
Alternatively, find the difference of the the integral of sqrt(4-x^2) over the intervals [1,2] and [0,1] and add 1.
Si llamamos T a la proyección ortogonal de Q sobre BG→ QT=1 y QB=2→ El ángulo QBG=30º→ Por simetría, el ángulo en B está trisecado y PBQ=30º→ BT=√3→ CQ=√3 -1 → Área verde = (⊓2²/12)-2(1*CQ/2) =(⊓/3)-(√3 -1)=(⊓/3)+1-√3 =0.3151
Gracias y un saludo cordial.
Thanks❤️🌹
Since DB = 1 and the hypotenuse BP = 2, △DBP is a special 30° - 60° - 90° triangle ⇒ PD = √3.
By symmetry, △BCP ≅ △BCQ with a base of √3 − 1 and a height of 1 for a total area of √3 − 1......➀
Since the right angle ABG is trisected, the area of the circular sector BPQ is ¹⁄₁₂ π 2² or ⅓ π .........➁
The green shaded region is ➁ − ➀, that is ⅓ π − (√3 − 1) or 1 − √3 + ⅓ π ≈ 0.315 square units.
I would use calculus for this
شكرا لكم
ليكن Xهو المجهول
و s مساحة القطاع الدائري PBQ
وb مساحة المثلث PBQ
وC مساحة المثلث PCQ
إذن X=s-b+c
X=pi/3 +(1- جذر 3)
A = 0.315
Procedo con geometria e integrali ..π/3-(√3-1)
Thanks ❤️🌹
I resorted to using integral calculus to reach the same result.
1st Comment
1st view
Super ❤️🌹