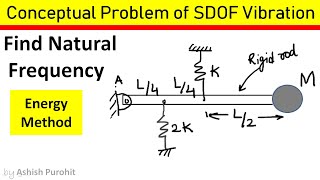
Problem 2 7 Finding Natural Frequency of massless bar and mass at end
HTML-код
- Опубликовано: 8 фев 2025
- MECHANICAL VIBRATIONS
Images from S. Rao, Mechanical Vibrations, 6th Edition
Video by Carmen Muller-Karger, Ph.D
Florida International University
Natural frequency of mass springs systems, finding the equation of motion, equivalent constant of the spring








You saved my degree, utmost respect for putting in the time to explain this for my vibrations exam!
I am very glad I could help!.
Indians attendance here ❤❤❤❤
Thankyou this cleared my doubt in a problem from physics galaxy
Thanks so much 🙏
how to make videos like this
i want to start a channel like this
solving mechanical engineering problems
thank u very much!!!!
Instead of doing the similar triangles approach, can you just work in terms of angular displacement or would that not be correct? Many thanks
yes, you can!
The videos are not clear 😢
How can I help?
If the bar had a mass, would you need to equal the first equation of motion to (Moment of inertia of the bar)(Angular acceleration) ? Thanks for solving it helped a lot
yes, and the system becomes a two-degrees-of-freedom system. See videos for multi-degree of freedom systems.
@@cmullerk_Mechanics Thanks for the answer
On 8.45 there is a little mistake i think. It must be K3.K2.l2^2/l3^2 but you wrote K3.K1.l2^2/l3^2 am i wrong? I will be very happy if you answer, thanks.
yes, you are right. Thank you for noticing that. I wrote it correctly after when I used k_eq to determine the natural frequency.
@@cmullerk_Mechanics Thanks for answer
Why don’t you consider beam stiffness? Is this reason about pin rotation?
The problem statement says that this is a rigid massless bar.
Oh, I understand. Thank you!
Could u please explain how does mg cancel out with the static deflection of the springs ?
The weight is a constant force that, for a vertical bar, only affects the deflection of the springs and does not contribute to the vibration motion. It only changes the equilibrium position of the system. If you measure the vibration respect to the equilibrium position this constant force will not appear in the response.
Which book you're referring to for alk of these lectures
Images and problems are from S. Rao, Mechanical Vibrations, 6th Edition. I added this information on the thumbnail of the video and description.
Why acceleration is exist? We put Angular acceleration is 0
Thx for video
Newton 's second law is f=ma, you have acceleration of the mass
Can i reach you please? I have a question and i couldn't solve it, maybe you can upload a video about that problem.
which one is the question? maybe I already solve it
All vibrating bodies have following DOF: a)1 b)2 )3 d)4
Please answer
Depending on how you model your system, you can have 1, 2, 3, etc DoF.