A Homemade Functional Equation | Math Olympiads
HTML-код
- Опубликовано: 7 ноя 2024
- 🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
/ @sybermathshorts
/ @aplusbi
⭐ Join this channel to get access to perks:→ bit.ly/3cBgfR1
My merch → teespring.com/...
Follow me → / sybermath
Subscribe → www.youtube.co...
⭐ Suggest → forms.gle/A5bG...
If you need to post a picture of your solution or idea:
in...
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries #sequence
via @RUclips @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Number Theory Problems: • Number Theory Problems
Challenging Math Problems: • Challenging Math Problems
Trigonometry Problems: • Trigonometry Problems
Diophantine Equations and Systems: • Diophantine Equations ...
Calculus: • Calculus



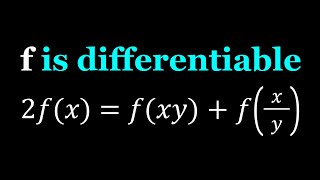





Absolute legend. Never stop making these ❤
Man, this is like your third video today. Wish i had your energy
And his passion too.
Hehe thanks 😍
😍
I just wrote x/3+2/x as (x^2+6)/3x then expressed Right hand side as (x^4+36)/18x^2 and then used formula for (a+b)^2 to simplify and replaced (x^2+6)/3x by z then finally replaced z by x
3rd 😇 See that x²/18 + 2/x² is "almost" (x/3 + 2/x)² so try to rewrite the rhs into a form that contains (x/3 + 2/x)².
Like so: x²/18 + 2/x² = ( x²/9 + 4/x² ) / 2 = ( x²/9 + 4/x² + 2∙2/x∙x/3 - 2∙2/x∙x/3 ) / 2 = ( x/3 + 2/x )² / 2 - 2/3.
So we have f( x/3 + 2/x ) = ( x/3 + 2/x )² / 2 - 2/3. Now we can finally re-label the argument and get f(x) = x²/2 - 2/3 😊
Nice!
The original expression has a reduced domain, |x/3+2/x|>=2sqrt(2/3)
you can see that a few ways
f(x/3+2/x)=(1/3)(x^2/6+6/x^2)=(2/3)cosh(ln(x^2/6))
cosh(real)>=1
so f(x/3+2/x)>=2/3
Yup!
This solution is valid only within (x/2 + 3/x)'s range:
prnt.sc/65opaMmhKgJT
Namely, any function f: R -> R that can be restrictable to the said solution within (x/2 + 3/x)'s range is a solution too.
For example, f(0) may take any value as the original condition does not apply to zero.
Exactly! There are actually an infinite number of functions satisfying the given property, unless f's domain is restricted to (x/3 + 2/x)'s range.
Sybermath's second method is MUCH easier and quicker.
Let u =x/3 and v=2/x then uv = 2/3
Substituting f( u + v) = ( u^2 + v ^2)/2
= ((u+v)^2)/2 -uv = ((u+v)^2)/2 - 2/3
Replace u+v with x then f(x)=(x^2)/2 - 2/3
Ok I guessed it will be x²/2 but don't know how tf constant came I will watch now
Got it silly me forgot about the 2ab term after squaring
Hold on: x/3 + 2/x is not 'onto'.If |t| < sqrt(6)/3 + 2/sqrt(6), f(t) is not defined. Your analysis holds only for |t| >= sqrt(6)/3 + 2/sqrt(6)
F.i.; f(0) is not defined. Which x do I have to chose such that x/3 + 2/x = 0?
I would love to see the responses to this.
Exactly! There are actually an infinite number of functions satisfying the given property, unless f's domain is restricted to (x/3 + 2/x)'s range.
>> "f(0) is not defined"
Rather you should say _f(0) is unconstrained it could be anything_
@@RUclips_username_not_found true, but im not writing a paper for the ams here ;-)
I just solved this in like 10 seconds and you did a 10 minutes video on this??
Let u = x/3 + 2/x then (u^2)/2 = (x^2)/18 + 2/(x^2) + 2/3
So f(u) = (u^2)/2 - 2/3. Done
congratulations! this channel is mainly for mortals :D
😄