¿¿¿PUEDES SUSTENTAR TU RESPUESTA CON UN MÉTODO???🧠🧠 ¡¡sin tanteo!!
HTML-код
- Опубликовано: 9 фев 2025
- UNETE GRATIS A NUESTRO CANAL DE TELEGRAM:t.me/boost/mate8a Si deseas crecer más en las matemáticas mira estas listas: • nivel monstruo matematico DONACIONES: PAYPAL: paypal.me/carl... PERÚ Mi número de cuenta BCP Soles es 25502336763002.
Mi número de cuenta interbancaria es 00225510233676300288. YAPE:996979664 CRIPTOMONEDAS USDT: binance 6J7P9LvgjKDjsf1vJgBKX9v4mryvSgKtDvHFySShPEne QUANFURY:4dA9CLwa7Yn5W8ERPE7o1kymcRdzALMpfKxpn7fSScb9



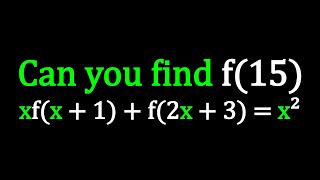





UNETE GRATIS A NUESTRO CANAL DE TELEGRAM:t.me/boost/mate8a Si deseas crecer más en las matemáticas mira estas listas:ruclips.net/p/PLN8VSugoTSIz2exC91mxHhsL3Q6FetfB8&si=iRVnssNFDqpuOSZxruclips.net/p/PLN8VSugoTSIw--pS4oGbWFXy-Wsn0hcS1&si=Fc0tK4WdQx11NRA-ruclips.net/p/PLN8VSugoTSIwLVxln2ll_cqIAogtzUusn&si=i993gW6GI7dHqOTW DONACIONES: PAYPAL: paypal.me/carlosov8a?country.x=PE&locale.x=es_XC PERÚ Mi número de cuenta BCP Soles es 25502336763002.
Mi número de cuenta interbancaria es 00225510233676300288. YAPE:996979664 CRIPTOMONEDAS USDT: binance 6J7P9LvgjKDjsf1vJgBKX9v4mryvSgKtDvHFySShPEne QUANFURY:4dA9CLwa7Yn5W8ERPE7o1kymcRdzALMpfKxpn7fSScb9
Para evitar la función de Lambert:
3¹¹ = (11-x)•3^(11-x)
9•3⁹ = (11-x)•3^(11-x)
Por similaridad, notamos que para que esto se cumpla:
11 - x = 9
x = 2
@@waylluq gracias por su comentario 🧠✋
Buen trabajo. Excelente.
@@EstebanChacon-e3e muchas gracias 🧠🧠🧠
Bien resuelto
Saludos desde perú🧠✋desde donde me escribes. Espero que estés bien✋
@@mundomatematico2015 Desde España
Mi agradecido, muy bien explicado muchas gracias
@@victor82942 muchas también a ud un saludo desde lima perú ¿ desde donde me sigues??🧠✋
Buenísima tu explicación. No conocía esa función.W. Puedes poner más ejercicios de este tipo porfa???
Hay varios en mi canal que he publicado recientemente. Puede dar una mirada al canal y verá......🧠✋👌muchas gracias x su comentario. 🧠🧠
Osea, se sabe la respuesta, el problema es como explicarlo, gracias profe
@@Gabriel-e9p9b así es🧠🧠🧠✋✋✋
Bd prof inca espero este recuperado de su salud.monte un video con esta ecuación exponencial:x^3-x-4=0.ssaludos desde la tierra de Bolívar.
Bien mi estimado saludos gracias x su paciencia 🧠🧠🧠🧠👌✋❤
Una ecuación que puedo resolverlo en tres segundos, Por qué demoraría media hora ??.. El tiempo es ORO !..
@@firefull8205 bien genio un saludo. Recuerda que es un tutorial no examen de admisión ✋✋✋🧠
@@mundomatematico2015
Disculpa, pero no es arrogancia, es practicidad, vivimos en un mundo en el que no podemos perder tiempo, ni siquiera "aprendiendo", sino, dando respuestas correctas en el menor tiempo posible, siendo evaluados permanentemente y, todo vale!.. Es solamente iterar el valor de "x" y al segundo siguiente tienes el valor correcto.. Si claro, si se trata de enseñar el uso de la función "W" sirve muy bién tu ejercicio, pero, por lo menos busca que el valor de "x" sea fraccionario, no entero, por lo demás, te felicito por tu empeño y tu dedicación, tu si mereces el título de "GENIO"..
@firefull8205 se repeta su opinión 🧠✋
Este ejercicio ...me resultó muy complejo - teniendo presente ...que seguro me faltan conceptos ..- pero VALORÓ MUCHO SU PACIENCIA Y DEDICACION ¡¡-
@josealbertogeiorgi8338 muchas gracias por tu respuesta 🧠✋
Hola. No sé dónde fue mi comentario anterior.
En el minuto 10:26 observo que de nuevo vuelve a sacarse un conejo de la chistera.
Convenientemente ha descompuesto
ln(3) · 3¹¹ = ln(3) · 3² · 3⁹
de tal manera que la función W de Lambert se resuelve de manera inmediata.
Pero sigue sin explicar cómo ha sabido que había que descomponer 3¹¹ como 3² · 3⁹, con potencias 2 y 9.
¿Por qué precisamente esas dos potencias? ¿Cómo lo supo?
¿Por qué no usó 3 y 7?
¿O bien 4 y 6?
¿O bien 5 y 4?
Lo que usted ha hecho es un cálculo mental QUE ES EQUIVALENTE EN DIFICULTAD a resolver la ecuación de partida.
No debería insistir en tropezar de nuevo con la misma piedra.
El argumento es simple:
Dado un problema original que se pretende resolver, en un punto concreto de su desarrollo se necesita resolver un subproblema, que es idéntico o equivalente en complejidad, a dicho problema original.
Es como utilizar la definición de un objeto dentro de la propia definición de dicho objeto.
ES UN RAZONAMIENTO CIRCULAR.
Usted debe tener claro que la función W de Lambert se resuelve mediante tanteo o métodos numéricos, salvo algunos casos triviales que todos conocemos de memoria, W(0)=0, W(e)=1, W(-1/e)=-1
Debe asumir que ES IMPOSIBLE CALCULAR LA FUNCIÓN W DE LAMBERT DE FORMA DIRECTA, SIN REALIZAR TANTEOS O LOGRAR APROXIMACIONES MEDIANTE MÉTODOS NUMÉRICOS.
Si usted en mitad del ejercicio realiza un tanteo algebraico, llamémosle truco, para calcular W(ln(3) · 3¹¹) para resolver la ecuación W(ln(3) · 3¹¹) = (11−x)·ln(3) es equivalente a resolver el ejercicio, 3ˣ + x − 11 = 0. SON PROBLEMAS EQUIVALENTES PUES LOS DOS REQUIEREN TANTEO Y TIENEN LA MISMA COMPLEJIDAD.
@@antonionavarro1000 agradezco tu comentario. Saludos✋✋✋🧠🧠🧠