Solving exponential equations with different bases
HTML-код
- Опубликовано: 5 ноя 2024
- How do we solve exponential equations with different bases? Oh well, make the bases the same first! Sometimes it's easy, sometimes we might have to use a log property that b^logb(x)=x
Subscribe to @bprpmathbasics for more fun algebra videos!
Get a blue e t-shirt 👉 bit.ly/blue2718
Get a 1.618 t-shirt 👉 bit.ly/1618shirt
Use "WELCOME10" for 10% off
-----------------------------
For more official SAT practice problems, check out 👇
• SAT math questions fro...
Download & try the official SAT practice tests on College Board here: 👇satsuite.colle...
-----------------------------
If you find my channel helpful and would like to support it 💪, then you can
support me on Patreon: 👉 / blackpenredpen
or buy a math shirt or a hoodie: 👉 blackpenredpen...
-----------------------------
"Just Algebra" (by blackpenredpen) is dedicated to helping middle school, high school, and community college students who need to learn algebra. Topics include how to solve various equations (linear equations, quadratic equations, square root equations, rational equations, exponential equations, logarithmic equations, and more), factoring techniques, word problems, functions, graphs, Pythagorean Theorem, and more. We will also cover standardized test problems such as the SAT. Feel free to leave your questions in the comment!
Subscribe for future algebra tutorials 👉 bit.ly/just_al...
-----------------------------
#justalgebra

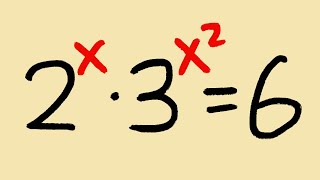






for the second equation I did,
(2^4x) x 2 = 3^x
(16^x) x 2 = 3^x
(3^x)/(16^x) = 2
(3/16)^x = 2
Taking log base (3/16) on both sides
x = log base 3/16 (2)
x = -0.414 (which is the same as yours)
great problems, looking forward to more!
I like how this was explained so clearly and simply. Crisp, without needless complications.
He teaches better in one second than many teachers in 1 hour.
2:00 his humor is crazy
It's cool how the answer to the second one still has 1,2,3,4 in it.
so that's when "log that's not base e" is important 😮
I'm some of my computer science classes, lg was used as a convention for log base 2.
I am highly impressed sir
"Surprising, right?"
Hahahaha
Well explained
(3x+1)log2 = xlog4
3xlog2 + log2 = xlog4
3xlog2 - xlog4 = -log2
x(3log2-log4) = -log2
x = -log2/3log2-log4
I love this guy. It's just funny because if he would have just took the ln of 2 and 3 in the first place he wouldn't have to re-write the answer
It also the x is ²log (3/16)
I did a more tedious method and got log2/log3-log2(4) which is still correct
i just used the property of logarithms, where you put the exponent in front of the logarithm
That is a good one!!!
(4x+1)ln2=xln3
4xln2+ln2=xln3
xln16+ln2=xln3
ln2=x(ln3-ln16)
x=ln2/(ln3-ln16)
Im supposed to solve using only natural log. that has been my problem finding examples of people solving with that and not log! Stuff like 2^(5x+4)=3^(3x-2) can you just write ln instead of log?
Since we have the change-of-base rule, it is arbitrary whether you write ln(8)/ln(2) or log(8)/log(2). Both produce the same result. You can solve any problem involving logs, using either natural log or log base ten. Or even some completely different base like log base 2.
To do the problem you provided using natural log:
Given: 2^(5*x+4) = 3^(3*x - 2)
Take the natural log of both sides:
ln(2^(5*x + 4)) = ln(3^(3*x - 2))
Use the log property, ln(a^b) = b*ln(a) to pull the exponents out in front:
(5*x + 4)*ln(2) = (3*x - 2)*ln(3)
Expand, move constants to the right, and variables to the left:
5*x*ln(2) + 4*ln(2) = 3*x*ln(3) - 2*ln(3)
5*x*ln(2) - 3*x*ln(3) = -2*ln(3) - 4*ln(2)
Factor the left:
[5*ln(2) - 3*ln(3)]*x = -2*ln(3) - 4*ln(2)
Isolate x:
x=[-2*ln(3) - 4*ln(2)]/[5*ln(2) - 3*ln(3)]
This can simplify to:
x = -ln(144)/ln(32/27), which evaluates to about -29.25
crazy guy
What is 2 log base2 of 3
I shouted NO ******* WAY for the second equation
Nice Shoes and nice video also
Beautiful
Those nikes bruh
wow