A Nice Mathematics algebra problem | Olympiad Question | Exponential problem | x=?

#quantativeaptitude #maths #olympiad#exponents#exponents #integral#rational
World math olympiad question | can you solve this? | can you solve this math problem,can you solve this challenging problem?,can you solve this equation,can you solve this puzzle,learn how to solve this challenging problem,can you solve this maths puzzle,math olympiad algebra problem,how can solve this puzzle,math olympiad problem,olympiad mathematics,math olympiad problems,mathematics olympiad,mathematics

[@HuzaifaKhan-m3i]

❤❤❤❤❤

[@AfsarSaid-f8s]

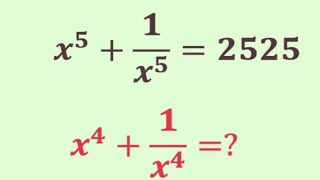
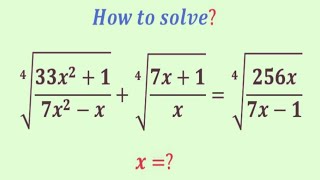
Good question

[@NaeemKhan-q6w1v]

Good

[@SrisailamNavuluri]

1040=16(65)=2^4(81-16)=2^4(3^4-2^4)=6^4-4^2
9+1/x=6,1/x=-3,x=-1/3
7+1/x=4,1/x=-3,x=-1/3.

[@SidneiMV]

8 + 1/x = u
(u + 1)⁴ - (u - 1)⁴ = 1040
u⁴ + 4u³ + 6u² + 4u + 1
- (u⁴ - 4u³ + 6u² - 4u + 1) = 1040
8u³ + 8u - 1040 = 0
u³ + u - 130 = 0
u³ - 125 + u - 5 = 0
(u - 5)(u² + 5u + 25) + (u - 5) = 0
(u - 5)(u² + 5u + 26) = 0
u = 5
8 + 1/x = 5
*x = -1/3*

[@RealQinnMalloryu4]

(3^2+/x)^2^2 ➖ (3^4+/x)2^2 (1^1+/x)^1^1 ➖ (3^2^2+/x)^1^1 (3^1^2+/x)^1 (3^2+/x) (x ➖ 3x+2).

[@Ismailorakzai-u1m]

❤❤❤❤❤❤