Let's Solve A Functional Equation | 2nd Method?
HTML-код
- Опубликовано: 8 сен 2024
- 🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
/ @sybermathshorts
/ @aplusbi
⭐ Join this channel to get access to perks:→ bit.ly/3cBgfR1
My merch → teespring.com/...
Follow me → / sybermath
Subscribe → www.youtube.co...
⭐ Suggest → forms.gle/A5bG...
If you need to post a picture of your solution or idea:
in...
#algebra #functionalequations #functions
via @RUclips @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Number Theory Problems: • Number Theory Problems
Challenging Math Problems: • Challenging Math Problems
Trigonometry Problems: • Trigonometry Problems
Diophantine Equations and Systems: • Diophantine Equations ...
Calculus: • Calculus
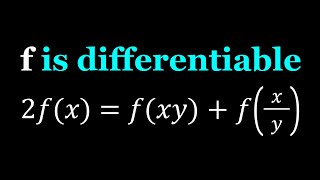








My friend (I still don't know your real name, Sybermath 😢), I absolutely LOVE your videos; and you're such a talented mathematician. Please, my friend, keep it up. THANK YOU! ❤
Np! Thank you so much 😀
For anyone familiar with hyperbolic functions and their inverses the result was quite expected because we have
cosh(u) = (eᵘ + e⁻ᵘ)/2 = (e²ᵘ + 1)/(2eᵘ)
If we set cosh(u) = x and we want to find an expression for the inverse function arcosh(x) = u in terms of x we can set eᵘ = t which then gives (t² + 1)/(2t) = x or
t² − 2xt + 1 = 0
So t = x ± √(x² − 1). For the domain ℝ the range of the cosh function is [1, ∞) so the domain of arcosh is [1, ∞), that is, x ≥ 1. Both values of t = x ± √(x² − 1) are real and positive for x ≥ 1, so, since eᵘ = t implies u = ln t we get two values u = ln(x ± √(x² − 1)) which are each others opposite since the product of the roots of the quadratic in t is 1. This is because cosh is an even function and therefore not invertible if we take ℝ as its domain.
If we restrict the domain to [0, ∞) then cosh(u) = x with u ≥ 0 and then the function is invertible and we have u = ln(x + √(x² − 1)) and therefore
arcosh(x) = ln(x + √(x² − 1))
for x ≥ 1.
We could use this to solve the functional equation
f(x + √(x² − 1)) = x
in a single line, because if we set x + √(x² − 1) = t and t = eᵘ then x = cosh(u) = (e²ᵘ + 1)/(2eᵘ) = (t² + 1)/(2t) so f(t) = (t² + 1)/(2t). This, however, supposes that x ≥ 1.
Note that since t = x + √(x² − 1) and t = x − √(x² − 1) both imply x = (t² + 1)/(2t) the functional equation
f(x − √(x² − 1)) = x
has the same solution f(t) = (t² + 1)/(2t) but that for |x| ≥ 1, x + √(x² − 1) can only take values on [−1, 0) ∪ [1, ∞) and x − √(x² − 1) can only take values on (−∞, −1] ∪ (0, 1]. This is in agreement with the fact that, considered as a real function, f(t) = (t² + 1)/(2t) has the domain ℝ\{0} and the range (−∞, −1] ∪ [1, ∞).
If we have x ≤ −1 and we set x + √(x² − 1) = τ then τ is negative but then we have (−x) − √((−x)² − 1) = −τ = t where −x ≥ 1 and t is positive, so with t = eᵘ we then again have −x = cosh(u) = (e²ᵘ + 1)/(2eᵘ) = (t² + 1)/(2t) and therefore x = (t² + 1)/(−2t) = (τ² + 1)/(2τ) so f(τ) = (τ² + 1)/(2τ). This is a simple consequence of the fact that x + √(x² − 1) = t and x − √(x² − 1) = t both imply x = (t² + 1)/(2t).
Put "-x" in place of "x"
Now, add both equations..
You get,
f(x+√{x²-1}) = - f(-x+√{x²-1})
=> x+√{x²-1} = x-√{x²-1}
=> x²-1=0
=> x=±1
Domain of original was x could not be between -1 and 1
For reals, yes. But, if you plot the absolute value (converting the coefficients of i) the graph is very interesting.
Yu are excellent. I suppose that you work with a team because it is imposible for me to think that only one person can solve and produce a lot of problems, that are sometimes very, very complex.
Thank you! I have a good number of friends who sometimes suggest problems but most of the time I'm by myself
You could also let x = cosθ and use Euler's formula
x = cost wouldn’t work as |x| >= 1. However you could x as sect
@@amanrishal5269 But that's exactly the reason it works out: the radical comes out to be ±isin(t), so the argument of the function is exp(±it). Now, on the right hand side you have cos(t), which is (exp(it) + exp(-it))/2; given that addition is commutative, if you consider exp(it) or exp(-it) for the argument on the left hand side the answer on the right hand side is always going to be (x+1/x)/2, which simplifies to (x²+1)/2x
Better use x = ch(t) since ch^2(t) - 1 = sh^2(t)...then if t>= 0 (hence x>0) x + sqrt( x^2 - 1) = ch(t) + sh(t) = exp(t); you end up solving f[exp(t)] = ch(t)...then if x
@@amanrishal5269I set x equal to secant theta..is that what you meant? But then how did you go from there?
Wow!!! Great idea ❤️😍
Thank you so much.... Master
You are very welcome
One interesting point is that although the function is defined on the reals for all nonzero x, the argument of the function in the functional equation is complex for |x| < 1. In fact, digging a little deeper leads to the observation that if x is a complex root of unity, then f(x) will be a real number on the interval [ -1, 1 ].
Actually, a minor correction: if x is a complex root of unity with a positive imaginary part, f(x) will be a real number on the interval [ -1, 1 ]. I have not characterized the function for the other half of the group complex roots of unity.
It is true that if f(z) = (z² + 1)/2z = ½(z + z⁻¹) and if z is a complex root of unity, then f(z) is a real number on the interval [−1, 1] but this is not just true if z is a complex root of unity but true for any z such that |z| = 1. In fact we have f(z) ∈ [−1, 1] if and only if |z| = 1.
To see this, assume that f(z) is a real number on the interval [−1, 1], then there exists a (real) θ such that
½(z + z⁻¹) = cos θ
which gives
z² − (2·cos θ)·z + 1 = 0
This quadratic equation has the solutions
z₁ = cos θ + i·sin θ
z₂ = cos θ − i·sin θ
So, for any complex number z with |z| = 1 we have f(z) ∈ [−1, 1] and, conversely, for any real number t ∈ (−1, 1) there exists a pair of conjugate complex numbers with modulus 1 such that f(z) = f(z̄) = t. In other words, the complex function f(z) = ½(z + z⁻¹) maps the unit circle onto the real interval [−1, 1]. If cos θ = 1 then the equation z² − (2·cos θ)·z + 1 = 0 reduces to (z − 1)² = 0 which has a double root z = 1 and if cos θ = −1 then the equation reduces to (z + 1)² = 0 which has a double root z = − 1. Since for any t ∈ (−1, 1) there exists a unique θ ∈ (0, π) such that cos θ = t and since sin θ > 0 for any θ ∈ (0, π) the complex function f(z) = ½(z + z⁻¹) bijectively maps the upper half of the unit circle onto the real interval [−1, 1] and since f(z) = t implies f(z̄) = t whenever |z| = 1 it also bijectively maps the lower half of the unit circle onto the real interval [−1, 1].
Addendum: since for any complex z we have |z|² = zz̄ it follows that for any z with modulus unity we have zz̄ = 1 and therefore z⁻¹ = z̄. Consequently, for any z such that |z| = 1 we have
f(z) = ½(z + z⁻¹) = ½(z + z̄ ) = Re(z)
and it immediately follows from this that f(z) bijectively maps both the upper half and the lower half of the unit circle onto the real interval [−1, 1].
Let x+sqrt(x^2-1)=u and x-sqrt(x^2-1)=z,and notice uz=1 so z=1/u. Now x=0.5(u+z)=0.5(u+1/u) so f(x)=0.5(x+1/x)😊
easy
That's a quadratic solution btw.
❤🙏🙏😀
❤️😍
Writing z = x + √ ( x^2 - 1)
z^2 - 2 z x + 1 = 0
x = z /2 + 1 /( 2 z)
f ( z) = (z + 1/z) /2
Let x = ch(y)
f(x + sqrt(...) = f( ch(y) + sh(y) ) = f(e^y)
Let e^y = t => y = ln(t) => x = ch(ln(t)) = [e^ln(t) + e^-ln(t)] / 2 = t/2 + 1/2t
f(t) = t/2 + 1/2t
But whats ch(x)?
@@Manisphesto hyperbolic cosine
ch(x) or cosh(x) = [ e^x + e^-x ] / 2
hyperbolic sine
sh(x) or sinh(x) = [ e^x - e^-x ] / 2
ch^2(x) - sh^2(x) = 1 => ch^2(x) - 1 = sh^2(x)
ch(x) + sh(x) = e^x
I tried this approach, too. Pretty satisfying!
Yes. But remember that x = cosh(y) implies x ≥ 1 so you have only solved the functional equation for x ≥ 1 whereas we can also have x ≤ −1.
Thank you, I finally understand why no one likes to make such substitutions.
WA -> f(t+Sqrt[Power[t,2]-1])=t solve f(t) for t=x+Sqrt[Power[x,2]-1]
it works 🤗🤗
This doesn't work for me in the online version. But my idea was that if we have
f(x + √(x² − 1)) = x
and since, assuming that f is invertible this implies
f⁻¹(x) = x + √(x² − 1)
this problem is really just about inverting this function, because the inverse of f⁻¹ is f. Therefore, I entered
invert x + sqrt(x^2 - 1)
in WolframAlpha and this immediately gave the result (x² + 1)/2x.