A beautiful log-trig integral featuring an important constant
HTML-код
- Опубликовано: 5 фев 2025
- Here's a nice log trig integral that evaluates to a famous value of the Reimann zeta function. Solution development using basic trig substitution and a beautiful series expansion of the natural log function.
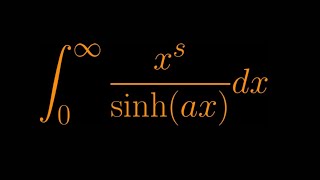







It's been a while since I sat my butt down and enjoyed a Maths 505 video, and I see I've got a bunch to enjoy.
❤❤❤
Really impressive solution. Smart substitutions, fascinating integral. Thanks for your selections and your attractive videos.
Nice video and beautiful result! As someone else pointed out in the comments, substituting u = ln(sin(x)) makes the calculation quicker because cotan(x)dx is simply du, you're left with the integral from -inf to 0 of u.ln(1 - e^2u). Then, series expansion and integration by parts yields the result quite quickly as long as you don't make as many sign errors as I did.
Exactly what I thought
Excellent, I didn't expect to see Apery's constant.
Finally an integral on my level
thank you for the confidence boost i now feel like Wolfram Alpha in human form
Well not every fascinating integral has to involve the polygamma functions😂
I love integrals, but this one was a bit too easy for my liking. I even figured this one out, and that’s saying something!
very well done
I expressed the integral as derivatives of the Beta function and evaluated a really long limit to get the answer
Same and it was awful
If you do a substitution by u=sin(x)^2, the ways to solve it is even better
I also solved in a same way......
It tooks the form of
[⅛{ln(x)ln(1-x)}/x]dx integrate 0 to 1.......
Then ln(1-x)= -(x/1+ x²/2 + x³/3 ......)
And then simply gamma function of logarithmic form
@@Anonymous-Indian..2003 I found it with the polylogarithms with the primitive of ln(1-x)/x
Can you just solve it by using ln(sinx)=t, all rest terms cancel out leaving just Jonquière's function
I'm not sure if I saw this somewhere already, but my first idea was to define I(A,B)=integral from 0 to pi/2 sin^A(x)cos^B(x)dx, then differntiate it one time with respect to A, and one time with respect to B, plug A=1 and B=-1, but you have to calculate two derivatives of beta function.
I'm not even sure, if that what would be legal strategy, convergence wise, just my first thought.
That was a video I made a while back😂😂😂
But you'll run into problems with the gamma function cuz you can't plug in negative 1
@@maths_505 Oh right, i thought i saw it somewhere else, but couldn't excatly place it where, nor was completely sure if it wasn't just a similar function, with additional terms. Nice video, by the way.🙂
gotta say this one is a bit easier than the other ones 😂 i managed to anticipate every step except for the infinite series expansion which i really should try to use more
Same I rarely use series expansions
Wow
I'm confused by one fact in many of your videos. You say that, in order to use the infinite series expansion of 1/1-u, |u| must be strictly less than 1. But the limits of integration comprise the case of u being exactly 1. Would not that be a contradiction and a limitation in the use of the expansion?
1 is an upper limit
Meaning that u approaches 1 from the left
0 is a lower limit meaning that you approach 0 from the right...
Nothing here actually equals zero or 1
They're just limits
If u take the integral from 0.000000001 to 0.9999999999, u would be fine. If u added a perturbation epsilon to both limit endpoints of the integral and let epsilon -> 0 , by continuity u would have convergence at the endpoints - and so this really isn’t an issue here
I would never overcomplicate this for myself by bringing in derivatives of the beta function
I almost got it right tho except I got -ζ(3)/8
Oh and did I mention I ended up using the tetragamma function at the very end
Every time you use IBP on the definite int[x^ylnx]dx, I scream internally.
int[x^ylnx]dx = d/dy int[x^y]dx
❤