
- Видео 62
- Просмотров 74 099
Coconut Math
Добавлен 5 окт 2013
Math videos focusing on intuitive explanations of high-level mathematical proofs. Knowledge of real analysis and abstract algebra is helpful, but not required. Recently I have been uploading more number theory content, which is probably more niche than previous videos, but hopefully it is still informative!
I often pick my own topics for videos but I am open to requests! If there is a problem you would like to see solved, feel free to comment or send me a message. I almost always solve problems that are suggested by viewers even if it takes me a bit to figure them out.
I often pick my own topics for videos but I am open to requests! If there is a problem you would like to see solved, feel free to comment or send me a message. I almost always solve problems that are suggested by viewers even if it takes me a bit to figure them out.
Видео
Galois group of x^4+x+2 over F_3
Просмотров 4884 месяца назад
Finding the Galois group of an (irreducible) polynomial over a finite field.
Galois group of x^5+x^2+1 over F_2
Просмотров 4184 месяца назад
Here we find a Galois group of a polynomial over a finite field.
Measure spaces with measure equal to 1 (Part 2: containment of L_p spaces)
Просмотров 414 месяца назад
We show that L_p spaces form a decreasing chain of sets whenever the total measure of our space is 1. We also find a condition for equality! (Which is quite hard)
Measure spaces with measure equal to 1 (Part 3: limit of p-norms as p converges to 0)
Просмотров 274 месяца назад
We prove an identity for p-norms as p converges to 0.
Measure spaces with measure 1 (Part 1: p-norms are increasing)
Просмотров 354 месяца назад
We prove that the p-norm is increasing in measure spaces with total measure 1, and find a condition for equality.
Basics of Galois Theory Part 4 (Intermediate Subfields)
Просмотров 6117 месяцев назад
Thanks for watching! en.wikipedia.org/wiki/Galois_group en.wikipedia.org/wiki/Fundamental_theorem_of_Galois_theory en.wikipedia.org/wiki/Abel–Ruffini_theorem
Basics of Galois Theory Part 3 (Examples continued)
Просмотров 6197 месяцев назад
Thanks for watching! en.wikipedia.org/wiki/Galois_group en.wikipedia.org/wiki/Fundamental_theorem_of_Galois_theory en.wikipedia.org/wiki/Abel–Ruffini_theorem
Basics of Galois Theory Part 2 (Examples)
Просмотров 7557 месяцев назад
Thanks for watching! en.wikipedia.org/wiki/Galois_group en.wikipedia.org/wiki/Fundamental_theorem_of_Galois_theory en.wikipedia.org/wiki/Abel–Ruffini_theorem
Basics of Galois Theory Part 1 (Galois groups)
Просмотров 1,3 тыс.7 месяцев назад
Thanks for watching! en.wikipedia.org/wiki/Galois_group en.wikipedia.org/wiki/Fundamental_theorem_of_Galois_theory en.wikipedia.org/wiki/Abel–Ruffini_theorem
Proof of Stirling's Formula, Part 3.
Просмотров 1419 месяцев назад
In this video we finish the proof by finding the value of the constant.
Proof of Stirling's Formula, Part 2.
Просмотров 949 месяцев назад
In this video we (almost) prove Stirling's Formula.
Proof of Stirling's Formula, Part 1.
Просмотров 2779 месяцев назад
In this video we investigate the properties of a sequence.
Galois group of x^5-4x+2
Просмотров 2,1 тыс.9 месяцев назад
Thanks for watching :) A slight correction: the orbit stabilizer theorem says that (size of orbit)x(size of stabilizer) = |G|. In the video I said the index of the stabilizer instead of the size, which is not true (although the basic argument is still the same).
The sum of a nilpotent and a unit is a unit
Просмотров 45110 месяцев назад
The sum of a nilpotent and a unit is a unit
Units of a polynomial ring (f(x) is a unit iff a_0 is a unit and a_1,...,a_n are nilpotent)
Просмотров 26710 месяцев назад
Units of a polynomial ring (f(x) is a unit iff a_0 is a unit and a_1,...,a_n are nilpotent)
Prove l^p is complete for p greater than or equal to 1
Просмотров 7310 месяцев назад
Prove l^p is complete for p greater than or equal to 1
Fractional parts of an irrational number are dense in [0,1)
Просмотров 20010 месяцев назад
Fractional parts of an irrational number are dense in [0,1)
Proof that Z[(1+sqrt(-19))/2] is not a Euclidean domain
Просмотров 40411 месяцев назад
Proof that Z[(1 sqrt(-19))/2] is not a Euclidean domain
Show that B/p is isomorphic to Bp/pBp
Просмотров 6611 месяцев назад
Show that B/p is isomorphic to Bp/pBp
Regular function on projective variety is constant
Просмотров 11611 месяцев назад
Regular function on projective variety is constant
The closed unit ball in C([0,1]) is not compact
Просмотров 49711 месяцев назад
The closed unit ball in C([0,1]) is not compact


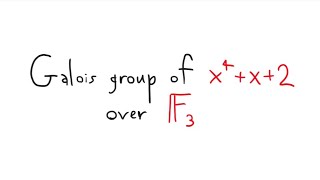
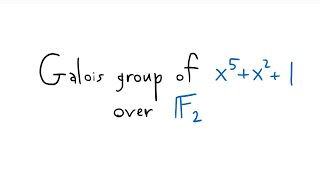





Hi, I'm pretty sure this solution is completely wrong.
Interesting...
Thank you!!
does this work for e^(conjugate of z)?
Critical point does not imply it’s zero.
Classic counter-example of Heine-Borel: compact = closed and bounded if and only if the space is of finite dimension. Which is not the case here. Also Riesz theorem: the closed unit ball is compact, iff same requirement.
Could you do the galois group of x^5-5x^2-3? and see if its a solvable group?
Great video! Appreciate your clarity and calm demeanor.
Fantastic video! Looking forward to more also!
Thank you for the informative video!
😮 Great video!
Great video! Thank you 😊
Fantastic! Thank you.
Awesome video!!
Great video!
Great vid!
I think a way to construct another polynomial not solvable by radicals from the proof. f(0)>0, f(1)<0, and limit to infinity show that f has at least 3 real roots Also, f’(x) has 2 real roots. Hence 𝑓 has exactly 3 real roots. Use this idea, with prime 3, f(x)=x^5-6x+3 is also not solvable by radicals
It is an example of polynomial that is not solvable by radicals
Thank you! That was exactly what I was looking for: a video explicitly computing the Galois group for specific polynomials.
Beautufully explained, very didactic. Do You know about a computer language that can draw the Sub Lattice Field using a library? [Matlab, Python, R]
Hey thanks! That's a good question, I bet you could find something on StackExchange. Maybe Matlab can do something like this
why wouldn't it be? algebraics contrast with transcendentals, which this clearly is not.
if you really wanna see something, consider the definition of e as expanded by the binomial theorem with respect to the Levi-Civita field. you'll find that by definition e cannot be Real, since its definition is a non-Real Levi-Civita series. this hints at a deeper fact, which is that there are no transcendental Reals, since by definition all transcendentals incorporate infinitesimals into their magnitudes, and infinitesimals are non-Real. this then means that the Reals are necessarily a subset of the algebraics, with the remainder being Imaginary or Complex, except that's not how anyone thinks of it, because e and pi, etc. are dumbly asserted to be Real because their gross magnitude is not infinitesimal. there's nothing about v5 or i that poses any issue, those are both totally ordinary algebraics. the interesting thing is that the underlying philosophy is broken because mathematicians have no idea how to apply rigor, and instead just say random crap like 'pi is a transcendental Real number' without any evidence and then it becomes unquestionable dogma for 130 years after the tools to demonstrate that it's nonsense have been available.
@@sumdumbmick sir, this is a wendys.
The field extension R/Q is not Galois. It’s not even algebraic.
Right... There is no Galois group R/Q. I guess the title means "the group of automorphism of R that fixes Q is trivial".
Yeah... I am debating whether I should reupload the video to fix that haha. "Aut(R/Q)" is probably better
Very cool, I used an ansatz of (x^3+AX^2+BX+C)(X^2+DX+E) = g(X) which leads to a contradiction fairly quickly. The rest is Theorems on finite Galois extensions that I'd probably have to revise :)
Hey, you can choose any finite field to prove polynomial irreducable or you need to guess 5?
Yes I think you can.
If you choose F_2 the polynomial becomes x^4+1, which is reducible because it has 1 as a root, so you do have to go slightly further to F_5. (F_3 doesn't work either)
Very nice. Another way to check that h is irreducible is with the Rational Root Theorem (en.wikipedia.org/wiki/Rational_root_theorem ).
I came here to say this.
Yep, people always seem to forget about that theorem but you can definitely use it, I think I even used it in another video haha.
but could there exist a polynomial whose splitting field is R?
not a polynomial with coefficients in Q, since that polynomial would only have finite roots.
@@penguinlord3918 yeah that makes sense
I will agree with the existing comments :)
Okay so Galois theory has been a while for me, but my first thought was that can't be true because you have a sequence of field extensions like R>Q(i)>Q, and [Q(i):Q]=2 so [R:Q]=[R:Q(i)]*[Q(i):Q] = [R:Q(i)]*2 > 1, so the group cannot be trivial. I'm assuming my thought is wrong because that property only holds for actual Galois extensions, i.e. normal and separable, and R/Q isn't even algebraic to begin with, so all of those rules are out of the door immediately, is that it? You can still always define a/the Galois group as autos in the big that fix the small, but they're not Groups of Galois field extensions in the original sense. Is that right?
I'm assuming by Q(i) you mean Q adjoin i, in which case the inclusion R>Q(i)>Q doesn't hold because i is a complex number? It is definitely true that R is an infinite dimensional extension of Q, but that doesn't matter for the group of automorphisms because it's not a Galois extension (which I think is what you were getting at).
@@coconutmath4928 yeah excuse my monkey brain, I was looking for any extension of degree 2 from Q in R like sqrt(2), and took the one that doesn't even land in R, my bad. If anything it confirms my initial proposition: "Galois theory has been a while for me" 😄 So yeah imagine that entire argument with sqrt(2). And the answer is, the entire thing isn't galois, so we can't use arguments of degrees of towers..?
You only proved the splitting field of x^4+2 is contained in Q(i, \sqrt[4]{2}), not the other direction.
True, here's a quick explanation of why the other direction is true. If the splitting field were properly contained in K := Q(i,\sqrt[4]{2}), then because K is a degree 8 extension the splitting field would have degree less than 8 and therefore the Galois group would have size smaller than 8. By computing the Galois automorphisms directly though, you can see there are exactly 8 of them, because there are four ways to map \sqrt[4]{2} and two ways to map i to something. When I took Galois theory we started by doing splitting fields then talked about Galois groups, so I wanted to keep those topics separate, but it would probably have been more rigorous to talk about the Galois group here as well.
Hey bro, need some algebraic topology, moduler forms
Modular forms is a great idea. I will get some videos uploaded soon. Algebraic topology is something I might learn more about next year, in which case I will give that a shot on my channel :O
Try to make video to find intermediate fields
You can learn more about that here if you're interested: ruclips.net/video/HX-IfYxOui0/видео.html&lc=Ugyinyg1K4n2eaSiyyB4AaABAg&ab_channel=CoconutMath You can apply everything in that video to this problem by thinking about subgroups of G.
Thank you for all the examples! There is surely other good teaching material on this topic on RUclips available too but much of that seem to lack a sufficient number of examples. It is good to practise, over and over, through all these examples.
Thanks for the support! Yeah I mostly learned Galois theory stuff by just doing examples... then there are the theorems about algebraic closures etc. that are a lot harder to understand haha. Glad you're enjoying!
very clair and straightforward. thank you
very interessting and special videos because i notice that the other youtubers don't make an example for the galois theory they just make an introduction and don't care about the practice part don't stop bro we need you i'm waiting for your next video 🥰🥰🥰😘
That means a lot!! I will be back with more videos on this soon. I always appreciate suggestions for problems if you have any
Wonderful! Thank you, and please do not hesitate to make more videos about the basics (or even more advanced topics) of Galois theory.
Thanks very much for the support! In the near future the plan is modular forms (not sure exactly what yet) and more Galois theory problems (of which two were just uploaded).
More
OK :)
More
More
More
Really nice, thank you!
Thank you!
ln(x) is continuous on [1;2] -> uniformly continuous on [1;2]
Which software are you using to make videos
I use microsoft whiteboard and record with OBS studio. OBS is free and records via window capture. Whiteboard is not great but gets the job done haha
Thanks bro 👍 You are doing great job
Great
Thanks very much!
good explanation
Thanks :)
Great videos! Can you please collect related videos into playlists to help us to navigate your content?
Good idea, let me put some of the Galois theory vids together. Thanks for the support
Thanks so much! I didn't expect you to have only this much subs with such great explanations
Thanks very much! I think one reason is because the topics are niche. Only so many people who want to learn number theory/galois theory/etc. Hoping to get more in the future though
Sir, please help me
I can try, what is your question?
Sir, please share me your no
Very nice, Sir
👍
Nice stuff❤ BTW what will be the galois group corresponding it?
Thanks! Not sure if you found it already but there's a video about that on my channel.