Видео

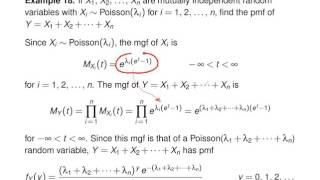
Nice

Who's here in 2024 with me😂

it was aksed in this year gate DA paper.. thanks for posting!

Thank you thank you thank you :)))

After probability videos, it would be good to continue with statistics videos...

this video sucks

Confused as why (n * (2/(2n-1))) is valid? (2/(2n-1)) is valid for first couple, shouldn't the remaining couples is (2/(2n-3)), (2/(2n-5)), (2/(2n-7))...?

I promise you’re the best 🙌

please please make more statistics videos

Your videos are so hepful. Can't thank you enough

Next time try something that doesn't scare the viewer coz wtf😂😂FR though

Are you still posting. I absolutely love this

great video

Thank you

Thanks Sir

Hello where can I get your textbook/ script?

Thank you so much ,this video is very useful because tomorrow is my presentation and I am so nervous but still waching this video then I am be confident for giving presentation again thank you so much

Wonderful lecture but sir what book are you using

Thank you for the well detailed explanation. Please what's the name of the book you are referring to?

Thank you so much. This helped a ton in my review!

Thank you so much you saved me

You didn't explain the topics, I don't get

if you can compile a playlist for multivariate analyis it would greatly help

Love this video! Thank you so much!

So grateful for information like this!

Thank you so much

Simply Awesome :)

Hi! Could you recommend me a bibliography where I can find this procedure and more detail? Thank you!

What's the final solution please?

Thanks

Do you know any distribution except geometric distribution 😡😡😡

Great work 👍

The thing I cant get it in the beginning is how two x1 and x2 data set creates mu1 and mu2 separetely. One Gaussian shape data set should have only one mean and sigma, right???

How do you write the likelihood for a multivariate Gaussian distribution with p correlation factor? Plus, imagine your data set is constructed by counts per channels as Gaussian shape histogram. Thanks.

How does the geometric proof account for the f(*) factor? This is not probability. The RVs are continuous so f(*) needs to be obtained by taking derivatives. How do you know the derivative works out with the fixed observation x_(k)?

Sec 3.5.2., page 204-205, "Introduction to Mathematical Statistics", 8th edition, Robert V. Hogg et al.

thanks sir

By appealing to the circular symmetry of the standard bivariate normal distribution, show how samples from a Cauchy distribution could be generated from independent N(0,1) samples

420 blaze

Sir,please refer me book for more numerical questions on transformation (discrete+continuous)🙏

Helpful 🙏

Thank you, Laurence.

Thank you so much! helped me greatly on my graduate level probability assignment!

Better than what my professor gave. Here's how he defined it: "Let X and Y be two random variables. We denote by E(X|Y = y) the expected value of the conditional distribution of X given Y = y. The conditional expectation of X given Y is denoted by E(X|Y ) and is defined to be E(X|Y = y) on the event Y = y." Kind of circular if you ask me.

Can you give me book

Great explanation 😇

This is so well explained.

Hi, which textbook do you use for this?

I am new in Statistics and what I need to understand may sound of very basic level. Yet I want to know it. On 0:02 why there are so many normal curves from x-axis and y axis? What do those curves signify?

can you share those notes