
- Видео 143
- Просмотров 402 189
Dr PK Math
США
Добавлен 21 мар 2020
Welcome to my RUclips Channel.
I am Dr. PK. With PhD in math, the goal is to give audiences high quality math problem solving skills so that they become familiarized with mathematics and enjoy math in the end.
➡️ So, let's start rocking!
I am Dr. PK. With PhD in math, the goal is to give audiences high quality math problem solving skills so that they become familiarized with mathematics and enjoy math in the end.
➡️ So, let's start rocking!
The Most Dazzling Integration Weapon
In this video, I am evaluating a challenging integral using contour method and residue theorem. Very challenging integral that can be evaluated in other methods, but I specifically used contour method and residue theorem to evaluate this integral.
#math #maths
Subscribe to Dr. PK Math here ⤵️
ruclips.net/user/DrPKMath
*************
✅ Follow Modern Dr PK Math on social media:
Instagram ▶️ drpkmath1234
Facebook ▶️ drpkmath
Twitter ▶️ drpkmath
*************
#math #maths
Subscribe to Dr. PK Math here ⤵️
ruclips.net/user/DrPKMath
*************
✅ Follow Modern Dr PK Math on social media:
Instagram ▶️ drpkmath1234
Facebook ▶️ drpkmath
Twitter ▶️ drpkmath
*************
Просмотров: 584
Видео
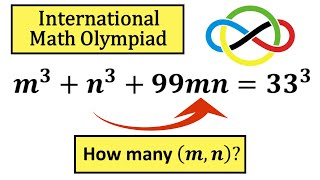
The Best International Math Olympiad (IMO) Algebra Problem I've Ever Solved
Просмотров 8974 часа назад
In this video, I am solving my personal best algebra problem from International Math Olympiad (IMO) using advanced algebraic skills. Very interesting algebra problem from International Math Olympiad. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitte...
Ivy League Math PhD Vs. The "Hardest" JEE Advanced Maths Problem
Просмотров 2,2 тыс.7 часов назад
In this video, I am solving the legendary limit problem from JEE Advanced Mathematics in 2016. With this problem, I am presenting the solution development using calculus and some series. Very tough JEE Advanced math problem but still fun to work! #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmat...
The Best Complex Equation I've Ever Solved
Просмотров 1,8 тыс.12 часов назад
In this video, I am solving the best complex equation I've ever solved by using Lambert W function. Such an interesting complex equation to solve with both real and complex solutions with the work through Lambert W function. Come check this interesting complex equation. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ...
The Ultimate Integration Weapon
Просмотров 3,8 тыс.21 час назад
In this video, I am evaluating a challenging integral using contour method and residue theorem. Very tricky integral that can still be evaluated with other methods, but I used contour method and residue theorem. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drp...
You Are Not Ready for Math Competition If You Do Not Understand This Problem
Просмотров 1,3 тыс.21 час назад
In this video, I am working on this interesting but challenging algebra/calculus problem from Harvard-MIT Math Tournament (hmmt) with @tibees. I solved this problem using knowledge of calculus and also advanced algebraic skills. If you want to know what Harvard-MIT Math Tournament is like, please watch the video by @tibees below ruclips.net/video/vhnlq0M8g5s/видео.html #math #maths Subscribe to...
2025 “Hardest" Korean SAT Suneung Math Exam - KILLER Calculus Question No. 30
Просмотров 1,4 тыс.21 час назад
In this video, I am solving the killer calculus question 30 from 2025 Korean SAT Suneung Math Exam that took place yesterday. This is a challenging calculus problem that requires advanced integration technique. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpk...
2024 “Killer" Korean SAT Suneung Math Exam Calculus Problem Q30
Просмотров 715День назад
In this video, I am solving a killer calculus problem from 2024 Korean Suneung CSAT Math Exam Q30. Very challenging calculus problem requiring advanced integral techniques. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
2024 "Hardest" Korean SAT Suneung Math Exam Killer Calculus Problem Q28
Просмотров 951День назад
In this video, I am solving the killer calculus problem from 2024 Korean Suneung CSAT Math Exam. Very challenging problem that a mixture of integration skills were required. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
The SAT Question Everyone Got Wrong
Просмотров 807День назад
In this video, I am solving an SAT math question that everyone got wrong. Come check the reason why, and what would be the right answer for this SAT math question. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
The Most Powerful Integration Weapon
Просмотров 1,1 тыс.14 дней назад
In this video, I am evaluating a challenging integral using Feynman's technique. Feynman's trick is introduced, evaluating this challenging integral in complex analysis. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
Life Changing Quadratic Formula
Просмотров 45814 дней назад
In this video, I am giving out a life time formula you can use either to factor out a quadratic function or get solutions of a quadratic equation without having to use a quadratic formula. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️twitter...
A Killer Calculus Problem from Korean CSAT Math Exam @MathRocks
Просмотров 49014 дней назад
In this video, I am solving a very challenging calculus problem to tackle with important integrals and integration skills. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
New Amazon Math Interview Question
Просмотров 87114 дней назад
In this video, I am solving an upgraded Amazon math interview question using more advanced level of calculus. Check this upgraded Amazon math interview, which is a lot cooler than the old Amazon math interview question. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ facebook...
The Hardest Integral on Internet
Просмотров 2,9 тыс.21 день назад
In this video, I am evaluating a very challenging integral using contour method along with residue theorem. Very difficult integral to evaluate with complex analysis. #math #maths Subscribe to Dr. PK Math here ⤵️ ruclips.net/user/DrPKMath ✅ Follow Modern Dr PK Math on social media: Instagram ▶️ drpkmath1234 Facebook ▶️ drpkmath Twitter ▶️ drpkmath
An Exceedingly Interesting Differential Equation
Просмотров 95321 день назад
An Exceedingly Interesting Differential Equation
You Are Not Ready for Calculus If You Do Not Understand This Problem
Просмотров 2,2 тыс.21 день назад
You Are Not Ready for Calculus If You Do Not Understand This Problem
Ultimate Integral with Gamma Function
Просмотров 75328 дней назад
Ultimate Integral with Gamma Function
Ivy League Math PhD Vs. Putnam Math Competition
Просмотров 3,6 тыс.28 дней назад
Ivy League Math PhD Vs. Putnam Math Competition
Fun Tetration Equation You Didn't Learn in School
Просмотров 751Месяц назад
Fun Tetration Equation You Didn't Learn in School
A Crazy Looking Binomial Integral from Cambridge Integration Bee
Просмотров 5 тыс.Месяц назад
A Crazy Looking Binomial Integral from Cambridge Integration Bee
A Breathtaking Differential Equation You Can Enjoy Solving
Просмотров 1,7 тыс.Месяц назад
A Breathtaking Differential Equation You Can Enjoy Solving
A Tricky Radical Equation to Find ALL Solutions from Harvard University
Просмотров 1,4 тыс.Месяц назад
A Tricky Radical Equation to Find ALL Solutions from Harvard University
A Surprisingly Interesting Differential Equation You Can Enjoy Solving
Просмотров 1,3 тыс.Месяц назад
A Surprisingly Interesting Differential Equation You Can Enjoy Solving
A Stunning Differential Equation You Can Enjoy Solving
Просмотров 902Месяц назад
A Stunning Differential Equation You Can Enjoy Solving
An Interesting Differential Equation You Can Enjoy Solving
Просмотров 1,8 тыс.Месяц назад
An Interesting Differential Equation You Can Enjoy Solving
The Best Differential Equation I've Ever Solved
Просмотров 11 тыс.Месяц назад
The Best Differential Equation I've Ever Solved
Can You Solve This Diophantine Equation from Harvard University?
Просмотров 1,7 тыс.Месяц назад
Can You Solve This Diophantine Equation from Harvard University?








Time for gaokao proffecor
Sir simply We can use ramanujan formula ∞ ∫((dx)/(xⁿ+1))=(π/n)/(sin(π/n)) 0
You are the king of integral professor
91181 by picking top and bottom sticks of the second digit and putting the first stick with the first digit to make it 9, and add the second stick after the last digit, this will make it 91181
This is such a nice video
大a
Great work as always professor🎉
You can also solve it by working backwards
I am curious, how can we work backwards?
@@iqtrainer Its a very tedious process(when I worte f^n(x) i meant f(x) interated n times) but instead we set f^10(x)= f(f^9(x))=1, so let f^9(x) = u, so u^2+sqrt(u^4+2u), you can see that there is only this part as u^2 is always less than sqrt(u^2+2y) and since it equals one we are looking for some u^2 less than 0.5. Let u= a + sqrt(b), but equating the radicals and integers, you will get = and do same process for f(f(8))=1/2(root(3)-1), where you will find 1= f^8(x), thus f^7(f(x))=1, thus f^7(x) equals pervious soliton and f^6(x)=1, obivisually the professor came up with much better way to solve problem
One easy way would to make (root(3)-1)/2 into 1/((root(3)+1), then we have u^2+sqrt(u^4+2u) = root(3)+1 and by inspection we u=1
Hello! I'd like to ask you to solve the question 3 of this paper (Suneung test - South Korea - I don't know what year). I don't know why, but RUclips removes my comment whenever I try to link the document, so I will type the problem: "There are 2 students from each of these countries: Korea, China and Japan. These 6 students will each randomly choose to sit in one out of the six seats numbered as in the diagram below. What is the probability that 2 students from the same country sit such that the difference between their seat numbers will be either 1 or 10" DIAGRAM (2x3 table): 11 ------ 12 ------- 13 21 ------ 22 ------- 23 Alternatives: a) 1/20 b) 1/10 c) 3/20 d) 1/5 e) 1/4 First off, I thought the exercise was asking about the cases where AT LEAST two students were sitting in such a way that the condition was satisfied, but I got to 13/15 (through combinatorics), which isn't even an option in the alternatives. Then, I shifted into thinking that maybe I should calculate only the cases where ALL OF THE 6 students were sitting in compliance with the condition and I finally arrived at 1/5 (letter D). Nonetheless, I couldn't find the official answer. So, I'd highly appreciate some help! Thank you!
Hello my friend. Thanks for the suggestions! I will find the paper and make a video solution for this problem very soon👍👍👍
To the people who are saying its "easy" try doing this in 2 mins + relatively same level of physics and chemistry
I know. Those peope who say it is easy are saying that because their low self-esteem. They could not solve this question and were so mad at themselves. So, that's the reason why they said it was easy because they could not solve it and hurt their ego
Hey there, I am from India, I don't know about you, but that's how I did it, (I am just a high-school student so if I did something wrong forgive me) ●divided top multiplication by n^n and multiplied by n! ●multiplied bottom multiplication by (n!)^2 and divided by n^2n ●then got that multiplication you got ~reimann uhh multiplication ●raised top and bottom term separately to the power of x/n like you write (a/b)^n =a^n/b^n, then raised the top and bottom half separately to the power of e by taking natural log on them ●next by the property of log and taking reimann sum, the top expression simplified to e^({integral}(1 to x) [ln(k)dk), here I figured that x is any contant integer, so I took x/n as my dk ●repeating above the bottom expression simplified to e^({integral}(0 to x) [ln(1+k^2)]dk), here also I took x/n as my dk as x is just any constant (but infinity as it would cause problems) ●The final expression becomes (e^(xln(x)-x+1))/(e^(xln(1+x^2)+2tan^-1(x)-2x)) ●I analysed the function for which I concluded that it's a decreasing function ●Further analysis showed me that the derivative is a increasing function ●So I got option a,c and d as correct options Please correct me if I got anything wrong 😅😅 Love from India ❤❤
good work
@ruslan8820 thanks, but I later realised that I took limit on the top part wrong, the reason my answer was wrong, It should have been 0 to x and the integral should be ln|1+k|dk
@@lazyobject5797 yeay , I agree , gj
Graphing the given equation will give you a line m+n-33=0 and a point (-33, -33). This is a very nice problem!
This one was indeed tough. Anyone who said this was easy without showing their work is a liar
You are the best integration master in RUclips. I know people on X know you are the best
This is so beautifully done professor, you are the best
The method you used to solve the first one was time efficient
Very super sir Still you are uploading such nice integrals It can be highly useful for me And provide more your techniques I wanted to learn!!👍🏻
Same thoughts with you
Gorgeous
Very nice!
I am innnnn loooove with your integrals, and your integration skills
Nice one by perfect professor
What a brilliant video
This is just the perfect video
Brilliant! I solved it very differently: First i set a=33 for convenience and so the equation became: A^3 = m^3+n^3+3amn. I substituted a = m+n+delta on both sides, so i got: (m+n+delta)^3 = m^3 + n^3 + 3mn(m+n+delta). Opening the brackets and subtracting both sides by the lhs and rhs of the original equation, all terms left had delta in them so delta=0 derives the set of m+n=33 solutions. Dividing by delta we're left with a quadratic equation whose determinant is -3(m-n)^2, which eliminates all solutions where m is not equal to n. Now substituting m=n in our original equation, we are left with: A^3=2n^3+3an. Now using the same trick: setting this time a=delta-n, simplifying we get: Delta^2*(delta-3n) = 0. So either delta is 0 which implies a=-n=-m which gives the last solution, or a=2n=2m which means m+n=a which is already covered in previous solutions. Overall, for a general non zero value of a: Either m=n=-a - one solution, or m+n=a, which implies all solutions (i, a-i) where min(a,0)<=i<=max(a,0) - a+1 solutions. A+2 solutions total. My choice of delta in each step was such that delta=0 was a relatively easy to see solution.
You are the best professor
Or just use from the start one of euler's identity a^3+b^3+c^3-3abc= {(a+b+c)[(a-b)^2+(b-c)^2+(c-a)^2]}/2 For a=m b=n c=-33
Isn't that vieta's formula?
@Min-cv7nt i learned it as a factoring method for a^3+b^3+c^3 my book said it was from euler but I couldn't find it on the internet
That is a most excellent idea! Thanks for pointing this out.
Fantastic video professor
What a brilliant and nice video professor
you have a talent to explain complex sums so easily…gives me a lot of motiv:)
I agree with you
Can you do ploynomial divison after you find the factor m+n-33 or no?
Yes, that's what I did.
I also did this too
you help me get a motivation for learning for my a-levels that are next year, im 13 and i love ur videos
I got lost at the 3rd step.
Do you mean the step starting at 2:30?
@@bjornfeuerbacher5514 1:43
@@MD-kv9zo He factors out n/1 from the first factor (x+n), which gives n/1 (1/n x + 1), then factors out n/2 from the second factor (x + n/2), which gives n/2 (2/n x + 1), and so on. In the end, this gives the product n/1 times n/2 times ... times (1/n x + 1) times (2/n x + 1) times ... And n/1 times n/2 times ... can be written as n^n / product of all k, with k going from 1 to n. And (1/n x + 1) times (2/n x + 1) times ... can be written es the product of all (k/n x + 1), with k going from 1 to n. In the denominator, he uses essentially the same steps.
@@bjornfeuerbacher5514 I got a bit confused at what was dividing what. Like (1/nx+1), does that mean ((1/(nx)) +) or ((1/n)x + 1), but I think I get it now.
@@MD-kv9zo Sorry, I should have written it clearer... I meant ( (1/n) x + 1) etc.
Why not the other arguments for each that differ by 2pi?
Nice and great. love this video a lot
Fantastic video professor. I know this hard limit question this is a famous one. But no one solved it like you. You are the best🎉
That was a tough question, but your clear and thorough explanation made it easy to grasp. Fantastic work, sir!
After watching ur usual videos, this does NOT match up to the level of "The hardest"
This question is not as hard as the other questions Dr PK usually solves?
This is an exam given by usual high school students... And also there r many more questions like this in paper which the student has to solve within time bound of 4-5 minutes which makes it the hardest ever
@@SamarthPatil-my5mh even so its not the "hardest", even for high schools, there much much more harder exams
@@SamarthPatil-my5mh yes I know, I'm preparing for JEE advanced myself lol. Don't keep the exam on a pedestal, there really are harder high school exams, but they don't boast about it. Heard of gaokao? Equally hard science questions and then you got Shakespearean literature (figuratively speaking)
@ I am surprised how there are so many ppl who dont know how to read. Title is "hardest" question from Jee Advanced maths, not the hardest "exam." Gosh. This question is one of the hardest questions in Jee advanced certainly. Whats wrong with you people
Hey in which uni/college do u work in Btw well explained
You are the best professor
Thank you so much my friend haha👍👍👍
What a fantastic video
Thanks a lot my friend👍👍👍
Sooooo handsome
Haha thanks a lot my friend for the compliment👍👍👍
This is really a nice video
Thank you my friend👍👍👍
Another nice video professor🎉
Thank you so much my friend haha👍👍👍
What a Clever method
Thank you so much my friend for your continued support👍👍👍
The Lambert W Function can be magical sometimes
@ true fellow geotuber
Make a series preparing for korean sat calculus questions
He already has a playlist for that in this channel
For sure my friend. I made a Playlist of Korean SAT exams. Please come check it out👍👍👍
What I would have done is used the fact that sin(x) = Im(e^ix) to deduce that I=integral from -inf to inf of sin(x)/(x^2-2x+5) wrt x= Im(J) where J= integral from -inf to inf of e^ix/(x^2-2x+5) wrt x, this way I only have to deal with one exponential
Nice idea! Thanks for sharing haha👍👍👍
Contour method is really cool, and smart in my opinion. But I wonder what are its limits.
Thanks a lot for your support my friend👍👍👍
Lol=8
Lol lol🤣🤣🤣
X, 2x-5=9
🤣🤣🤣🤣🤣
This is obviously very well-explained video
Haha thanks a lot my friend! Support means everything👍👍👍