
- Видео 6
- Просмотров 43 465
Enumerable
США
Добавлен 7 авг 2022
We make videos on counting and other mathematical topics. This channel was created during #some2, and is aimed at anyone who knows and/or loves the binomial theorem.
#combinatorics #math #maths
#combinatorics #math #maths
Trijections: Sometimes 3 is greater than 2 (#SoMEπ)
We prove two combinatorial identities using "trijections"--equivalence classes with size three--rather than standard "bijective" counting arguments. #combinatorics #trijection #bijection #math #somepi #someπ
The D.I.E. technique (for alternating sums): ruclips.net/video/aSu0OA40oWk/видео.htmlsi=wLOCMxDlgrMk28zz
Summer of Math Exposition: some.3b1b.co/
Music: Boreal - Asher Falero
Timestamps:
0:00 - Introduction
1:10 - First Identity
7:04 - Second Identity
10:39 - Equivalence Classes
10:56 - Challenge: Fermat's Little Theorem & Outro
The D.I.E. technique (for alternating sums): ruclips.net/video/aSu0OA40oWk/видео.htmlsi=wLOCMxDlgrMk28zz
Summer of Math Exposition: some.3b1b.co/
Music: Boreal - Asher Falero
Timestamps:
0:00 - Introduction
1:10 - First Identity
7:04 - Second Identity
10:39 - Equivalence Classes
10:56 - Challenge: Fermat's Little Theorem & Outro
Просмотров: 6 158
Видео
Dixon's Identity
Просмотров 9 тыс.6 месяцев назад
We prove Dixon's Identity using an elementary sign-reversing involution with exceptions. We also give combinatorial interpretations for binomial and trinomial coefficients. #combinatorics #involution #math The D.I.E. technique: ruclips.net/video/aSu0OA40oWk/видео.html Discussion of a combinatorial proof of Dixon's Identity: math.stackexchange.com/questions/338682/a-combinatorial-proof-of-dixons...
Proofs to D.I.E. For
Просмотров 4,4 тыс.10 месяцев назад
We cover the sign-reversing #involution trick of enumerative #combinatorics, also known as D.I.E.: Describe, Involution, Exceptions. From Art Benjamin and Jenny Quinn An Alternate Approach to Alternating Sums: A Method to DIE for: scholarship.claremont.edu/cgi/viewcontent.cgi?referer=&httpsredir=1&article=1581&context=hmc_fac_pub Learn about binomial coefficients: en.wikipedia.org/wiki/Binomial...
A Bell-Derangement Identity (#SoME3)
Просмотров 663Год назад
A combinatorial exploration of the distribution of fixed points of random permutations. This is a follow-up to "A Slightly Deranged Theorem": ruclips.net/video/YzCH3xR675c/видео.html We make use of Bell Numbers and Derangements. Submitted for the Summer of Math Exposition #some3. #combinatorics #math #maths #derangements #bell #bellnumbers A hint to the challenge problem: en.wikipedia.org/wiki/...
A Slightly Deranged Theorem
Просмотров 816Год назад
Given a random permutation, what's the expected number of fixed points? We give two proofs of the answer, one using the linearity of expectation and the other with a combinatorial argument involving derangements. #combinatorics #math #maths #derangements #probability
e ≤ 3 ...without calculus!? (#SoME2)
Просмотров 22 тыс.2 года назад
An injective/combinatorial proof that e is no greater than 3. Submitted for the Summer of Math Exposition #SoME2. Collaboration with tiusic.com/ Special thanks to: mobile. dontthinkmeat More on the binomial theorem: en.wikipedia.org/wiki/Binomial_theorem #combinatorics #math Due to a little miscommunication, we posted a duplicate video on Liam's channel: ruclips.net/video/myKkhVy74V4...


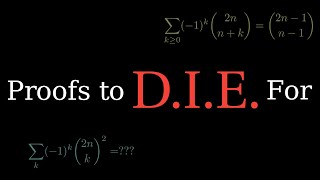


Negative weights! 🫠
No, babe! It's not what it seems. It's just a trijection, you see?
Isn't it 2 bijection in a row?
In case you only want to do algebra alone, the first formula can be derived by extracting terms of the function f(x)=(1+x)^(3n), simply calculate the average of function input roots of unity (z^3=1). This technique was demonstrated by 3b1b (Olympiad level counting)
I think I just found a perfectly good combinatorics channel, hope you keep it up as most seem to overlook these topics
I dunno buddy, is 3 greater than 2🤔
By ternary logic, the answer is "file not found."
@@nisonaticdamn
But wait, if n=1, don't we always just get one fixed point? Meaning that the variance is 0?
Yes! The formula we derived here only works for m ≤ n, and for a variance computation you'll need the 2nd moment, i.e. m=2. So yes, the variance will be 1 for n at least 2. And in that one case when n=1, the variance is indeed 0.
I... don't understand.
At 6:10 you can solve for D(n-k) directly by realizing that these derrangements must be the nth discrete differences of n!. That’s how I solved that problem one idle day. I can’t be the only one who’s seen that
Hang on. Did Did use cards for the bell numbers because one of the bell numbers is 52?
Huh...I didn't even notice that. Just a coincidence--like how C(14, 6)=C(15, 5).
@@enumerable345 C(14,6) equals C(15,5) because 10 times 9 equals 15 times 6.
A trijection is simply 3 bijections.
Isn't two enough? For sets A, B, C and bijections f: A -> B, and g: B -> C you have: - f^-1: B -> A - g^-1: C -> B - g•f: A -> C - f^-1•g^-1: C -> A
@@masonskiekonto590 No, if you do it that way you just have composition of bijections and the overall bijection is, while a bijection, is "fixed" in the sense that it has to follow gf. E..g, if h = gf then h(a) = gf(a). In the trijection we allow for an additional permutation/shuffling. It's like adding a 4th set D and then what you do will work. That is, with a trijection we are allowing for any h(a) != gf(a) but h(A) = gf(A) (and h be a bijection). That is, all around the triangle we want free bijections. If one is determined by the other we don't have the complete degree's of freedom that one expects from a trijection. (e.g., where there is no preferred starting point) Basically if you set h = gf in your example then imagine that, h is fixed but we find all possible bijections f and g then there is an h for each one. Call it H = {h | h = gf and f,g are bijections}. This set H is what we can choose for the 3rd side. if you let r ~ s mean r and s are bijections(on the same set). Then we want h ~ gf rather than h = gf. (we loosen the requirements that the map of the individual elements must be equal and only require the global nature of a bijection)
Ifff
Thanks for sharing it! 🙏📚🏆🥇🙏📚🏆🥇🇧🇷
🎉🎉🎉
The D.I.E. guy upload another video!!!
Not sure how I feel about that nickname. 😂
For even n, the second identity seems to sum to (-1)^(n/2)*C(n,n/2)/4^(n/2) or if we replace n with 2n (to clear most of the denominators), it would equal (-1)^n * C(2n,n)/4^n where C(n,k) is n choose k. I did not even attempt a counting proof of this, but I wonder how that would go...
I haven't fully worked it out, but I also figured it would be too much for this video. The counting argument would go something like... the trijection still cancels out most stuff. Then there are other mini-configurations we can put into trijection that also sum to 0 to cover more. Eliminate as many as you can this way, and the remaining configurations that don't balance all (this is a guess) have sign (-1)^(n/2). Count up the weights of anything that remains to get the RHS.
I love the Pascal triangle trick to figure out what you're looking at. Also, I know this sounds silly but so often I look at an identity and I go straight to counting lhs rhs, without actually stopping to think, what am I looking at and what is this identity saying! The way you broke down the first identity as 3 times every third item in the 3nth row of pascals triangle summing to the total of the row but it's over or undercounting has changed the way I will look at identities forever. Before diving into the problem, look at what the problem is asking. Thank you.
What a nice comment. Thank *you*, and keep counting!
why is 14 choose 6 equal to 15 choose 5
Was this in the video? At any rate, pretty easy to just plug in these values into the formula and see it is true.
14 choose 6 = 14!/(8!*6!)=15!/(10!*5!) * (10*9)/(15*6)=(15 choose 5) * 1
(n k) = n!/(n-k)!k! (14 6) = 14!/(14-6)!6! = 14!/8!6! = 14!•15/8!5!•6•15 = 15!/8!5!9•10 = 15!/10!5! = 15!/(15-5)!5! = (15 5)
@@KrasBadan amazing. can you use this to construct an equivalence between the two sets
@@MichaelDarrow-tr1mn Now can you find an equivalence which will always add a card to the 5 if all of them are lower than 15, while "splitting" the 15 into two cards that add up to 15 if 15 is part of the 5 cards.
Good video, but I don't like the terminology. A bijection uses bi- because it's both a injection and a surjection. That would suggest a trijection somehow adds another kind of -jection. I think "triple bijection" would be a better term for this relationship.
Well, it is kind of a jokey term, made up for this video. But-if you'll allow me to defend myself-I don't know that the Bourbaki group coined the word with the bi- prefix for that specific reason. An alternative, which generalizes better to tri-, is that there is a bijection between A and B if there's an injection from A to B and from B to A (Schröder-Bernstein), so a trijection would have a cycle of injections A to B, B to C, and C to A. Though this is motivated etymology on my part! :P
@@enumerable345 maybe we should worry about if that generalises to category theory properly too the equivalent of a bijection is an isomorphism, an injection a monomorphism, and a surjection an epimorphism, but it's not the case that a morphism that is both a monomoprhism and an epimorphism is automatically an isomorphism that makes me think that having a monomorphism from A to B and a monomorphism from B to A would not necessarily be the same thing as having a monomorphism from A to B that is also an epimorphism from A to B, but I don't know how to properly reason about this
man we all wanna reach samw height
Regarding the bonus problem: consider the set of all functions from Zp to Za, excluding constant functions. Now define an equivalence relation between two functions f and g if there is some x such that f(a) = g(a+x) for all a in Zp. One therefore sees that the equivalence classes are of size p, as they are all p cyclic shifts of the result. To show that all p are different, consider ftsoc some f where f(a+x) = f(a) [x ≠ 0] Then f(0)=f(x)=f(2x)=...=f((p-1)x). This is all the elements in Zp, hence f is constant. Contradiction. One could also imagine this as all sets of length p with elements from Za, which is the same.
Fourth!
Great video for a niche topic! Here's another problem which can be solved by a trijection. For any natural number n, prove that the sum of C(n + k, 2k) ⋅ 2^(n - k) from k = 0 to n is equal to (2^(2n + 1) + 1)/3, where C(a, b) = a! / (b! ⋅ (a - b)!).
Ooh, I don't think I've seen that identity before! I'll save coming up with the trijective proof for an upcoming plane flight. (Also--fellow Mudder?)
@@enumerable345 Yes I am a mudder, class of '13 :^) I shouldn't be too surprised you went to HMC, since you've clearly studied under Prof Benjamin.
nice
Incredible video !
Can you do a combinatorial proof that 10 choose 3 equals 16 choose 2?
almost forgot to mention, they're equal to 5!
Can you do a combinatorial proof that 5 plus 17 isn't 24? I seem to keep making that association for some reason
woah
I am officially amazed
Very very nice
If you can tell me where to find more such mathematical journals( like the one pinned in description of video) It would be great help.. Thank you sir.
Doesnt the mapping need to be bijective
The involutions match up some subset of the total set. Where they're not defined, we call those the exceptions.
i would rather DIE than count
Matching is so much easier than counting!
Nice presentation of a nice method. At @1:20, you mention a possible proof by Doron Zeilberger. You might be referring to his paper on Dyson's conjecture (now a theorem): sites.math.rutgers.edu/~zeilberg/mamarimY/zeilberger%20-%20a%20combinatorial%20proof%20of%20dysons%20conjecture%20-%20better%20scan.pdf.pdf. Dyson's conjecture contains Dixon's identity as a special case. Zeilberger cites a book by Cartier and Foata that has a combinatorial proof of Dixon's identity, but the book is in French, so I didn't read it.
I was here at 1k subscribers and less than 5k views.
These trinomial coefficients... (a+b+c a,b,c)=(a+b+c a)*(b+c b). This can be used to make many identities, such as the Team-Leader identity from the derangement video i think?
There are indeed tons of analogous identities/proofs with trinomial coefficients.
What software is he using to write the formulas and animate them ? Manim ?
Yep, Manim for everything!
Holy cow, this is a criminally under-subscribed channel.
That's amazing! That monstrosity at the end, well I had been bashing my head trying to understand the power series for the AGM iteration without using the integral technique, and it occurs there. And now I am wondering if that has a combinatorial interpretation, and more generally for hypergrometric identities
Very cool video, I love sign reversing involutions
I love homological combinatorics
Remove logical combinatorics lol
Me in my combinatorial class: DIE
Underrated 😂
It won't be wrong to call you Grant Sanderson of combinatorics (but I appreciate you as a unique individual and your efforts and time that you put to beautifully simplify maths) Should we expect to get a full playlist on combinatorics by you?
So kind, thanks! I definitely have ideas for a few more videos.
Another, easier practise problem: Look at subsets of {1,2,3,...,n}, such that the average is an integer, of length k. This is f(k,n). What is f(1,n)-f(2,n)-f(3,n)-...-f(n,n), evaluated with order of arithmetic from right to left?
That's a really cute problem! Thank you for sharing. Here is my solution, encoded with rot13. Gur qrfpevcgvba vf fhofrgf bs {1,...,a} bs nal fvmr jubfr nirentr vf na vagrtre, jurer gur fvta bs n frg vf qrgrezvarq ol gur cnevgl bs vgf fvmr. Gur vaibyhgvba, tvira n frg F jvgu nirentr n, vf whfg gb gbttyr gur cerfrapr bs n! Gur rkprcgvbany frgf ner gur frgf bs fvmr 0 naq fvmr 1. Gur fvtarq fhz bs rkprcgvbany frgf vf 1 - a, urapr gung vf gur jubyr fhz.
love your work.
No idea what I am watching, looks pretty though 🥺
Brilliant ...
Another vid, another banger 😮💨
Can you do pi being at least 3?
Pi is a very geometry-inspired number, so it's pretty easy to see geometrically. Imagine a unit circle circumscribing a regular hexagon. The circumference (2 pi) is larger than the perimeter of the hexagon (which is 6). This does require that a "straight line" is the minimum length curve between two points--which is a bit nontrivial. But just because it's geometric doesn't mean there's no combinatorial angle--I'll think about it!
What is the list of music used in this video
It's "Boreal" by Asher Fulero. I believe I looped it and slowed it down by about 20% for my use. That song is available in the RUclips Audio Library, so you can use it in your own videos easily.
sorry my guy but i think u forgot to end your sentence at 0:48. Or is it a play on showing the word description at that moment on the screen? In the sense that " link in the description". But before you also displayed " link in the ... " on screen. Are you afraid of the word description? Regardless of that I enjoyed the video and at the end it was clear to me the hows and whats, keep up the work !!
Yeah, that was supposed to happen--a sort of audiovisual joke. Thanks! I'm working on my next video, but there are a lot of new techniques I need to learn to animate it, so be sure to subscribe!