Power of a point | Proof by Geometry way
HTML-код
- Опубликовано: 6 окт 2024
- Power of a point | Proof by Algebra way
• Power of a point | Pro...
*****************************************
music
Moon | Prod.seekx
• [フリートラック] "Moon" hipho...
*****************************************








Take a cyclic quadrilateral ABCD and its circle's center O.
Draw lines from the radius to each point, OA, OB, OC, OD.
Due to the nature of circles, all of these lines have the length of the radius and are thus congruent.
Thus, the four triangles formed, OAB, OBC, OCD, ODA, are all isosceles.
Thus the triangles' base angles are congruent, with measures of w, x, y, z.
A = z+w, B = w+x, C = x+y, D = y+z.
Keep in mind that a quadrilateral's interior angles sum to 360.
Any convex quadrilateral can tile the plane, covering the entire 360 degrees around each vertex.
A quadrilateral can also be split into two triangles, whose angles sum to 180. 180+180 = 360.
Thus, 360 = A+B+C+D = (z+w)+(w+x)+(x+y)+(y+z) = 2w+2x+2y+2z = 2(w+x+y+z)
Any two opposite angles share no triangles, and thus have different angles, eg A = z+w, C = x+y
These opposite angles must sum to w+x+y+z. (The other pair of opposite angles must also sum to w+x+y+z.)
2(w+x+y+z) = 360 -> w+x+y+z = 180 -> A+C = 180
Opposite angles in a cyclic quadrilateral sum to 180.
Extend line AB to a segment AP. Vertex B now has an interior angle "B" and an exterior angle "PBC".
Since B and D are opposite angles, B+D = 180.
Since B and PBC are adjacent angles, B+PBC = 180. (If they weren't, ABP wouldn't be a "straight angle", a straight line.)
It should be clear that D = PBC.
An exterior angle on a cyclic quadrilateral is equal to its interior opposite angle.
This is the fact used at 0:42.
Also,
Because of this, the small and big triangles are similar.
To convince yourself, just look at them.
Mirror the little one and scale up by a factor s to get the other.
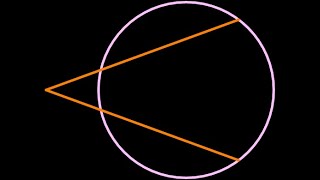
Let's say that segment PB has length b and PC has length c.
Thus, PA has length s*c, and PD has length s*b. (Remember, they're mirrored.)
This means that PA*PB = (s*c)*b and PC*PD = (s*b)*c.
Therefore, PA*PB = PC*PD.
So what?
What this is proving is that for any point P and any line PAB intersecting a circle, PA*PB is always the same for any line.
This gives two examples, PBA and PCD, and shows that the product is constant.
Since no angles were specified, it should be easy to see that we could have compared any and every two lines intersecting the circle.
Dear GOD isnt tbis way too mucj FUCJONG WIRK FOR ONE FUCKING little thing. Pardon ky language but isnt tbis why math is tedious and infurawhy.mdo all that workmfor one stuoid thing..and isnt there a faster and easier way of proving this? Thanks for your time.
And i dont see anyone thinking pf this unless they knew it beforehand do you? Thanks for sharing.
A very elegant proof ✨
And when the secant is tangent, the points A & B coincide at say point T(i.e. the point of contact) and (PA)(PB) = (PT)(PT) = PT^2
Hence, the power of point P = (PA)(PB) = PT^2
Nice simple animation of Circle Geometry 👍
🌏☯️🌌
Thanks -- nice video!
Perhaps would also be useful to do a video giving the proof of "Exterior angle of a cyclic quadrilateral".
you wouldn't have to if you know that opposite angles of a cyclic quadrilateral add up to 180°