A functional equation from the Netherlands.
HTML-код
- Опубликовано: 3 окт 2024
- We look at a problem from the 2001 Dutch Mathematics Olympiad.
Please Subscribe: www.youtube.co...
Merch: teespring.com/...
Personal Website: www.michael-pen...
Randolph College Math: www.randolphcol...
Randolph College Math and Science on Facebook: / randolph.science
Research Gate profile: www.researchga...
Google Scholar profile: scholar.google...
If you are going to use an ad-blocker, considering using brave and tipping me BAT!
brave.com/sdp793
Buy textbooks here and help me out: amzn.to/31Bj9ye
Buy an amazon gift card and help me out: amzn.to/2PComAf
Books I like:
Sacred Mathematics: Japanese Temple Geometry: amzn.to/2ZIadH9
Electricity and Magnetism for Mathematicians: amzn.to/2H8ePzL
Abstract Algebra:
Judson(online): abstract.ups.edu/
Judson(print): amzn.to/2Xg92wD
Dummit and Foote: amzn.to/2zYOrok
Gallian: amzn.to/2zg4YEo
Artin: amzn.to/2LQ8l7C
Differential Forms:
Bachman: amzn.to/2z9wljH
Number Theory:
Crisman(online): math.gordon.edu...
Strayer: amzn.to/3bXwLah
Andrews: amzn.to/2zWlOZ0
Analysis:
Abbot: amzn.to/3cwYtuF
How to think about Analysis: amzn.to/2AIhwVm
Calculus:
OpenStax(online): openstax.org/s...
OpenStax Vol 1: amzn.to/2zlreN8
OpenStax Vol 2: amzn.to/2TtwoxH
OpenStax Vol 3: amzn.to/3bPJ3Bn
My Filming Equipment:
Camera: amzn.to/3kx2JzE
Lense: amzn.to/2PFxPXA
Audio Recorder: amzn.to/2XLzkaZ
Microphones: amzn.to/3fJED0T
Lights: amzn.to/2XHxRT0
White Chalk: amzn.to/3ipu3Oh
Color Chalk: amzn.to/2XL6eIJ


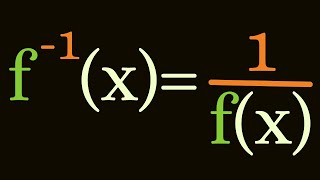






OK, today we learnt that the fancy name of telescoping sums is "Discrete Fundamental Theorem of Calculus".
It should be "Fundamental Theorem of Discrete Calculus". :-)
It's funny how mathematicians form "theorems" out of the most trivial things :D
Let's call "1+1=2" the "Fundamental Theorem of Elementary Addition" xD
@@dustinbachstein3729 Or say that 1+1 = 2 is the fundamental property of the number 2.
Yeah ... 99.9% of Algebra textbooks are saying that 😷: a simple telescopic sum ... maybe this guy is fan of Calculus over Algebra 🤣🤣🤣
@@csegura26 algebra book not gonna talk about calculus that's the reason.
As I found the values of f(1), f(2), f(3) and so on, I realized we were talking about triangular numbers. Then I wrote f(t) = t(t+1)/2 and proved that it satisfies the condition f(x + y) = f(x) + f(y) + xy. f(2001) follows easily from there.
That reasoning doesn't cut it though - you have to also prove that f(x) = x(x + 1)/2 is the only solution. A much more rigorous way would be to sub y = 1 combined with f(1) = 1 to find f(x + 1) = f(x) + x + 1, then prove that f(x) = x(x+1)/2 over all natural numbers by induction. Then f(2001) = 2001 * 2002/2 = 2003001
@@vietphan3767 I did it like this. Proving it is the only solution is not needed. If it satisfies the initial conditions, this is enough, since the problem implies a unique solution. Although you do not get a function with a real domain, it still is a reasonable solution.
Edit: the unique real solution is x - > int(t + 1/2) bounds 0 to x. The reason this is the only solution is that you can translate this to a discrete differential equation with starting condition.
Edit of edit: unique continuous differentiable (c1)
@@DrTaunu Sure, I'm just showing how an approach that will not be dismissed as guesswork by examiners should go, especially if it's required to find f(x) in any sub-domains of real numbers. Functional equations are really interesting in that sense - sometimes substitution is all that is needed, while in other times, there are additive or multiplicative properties that narrows down to integers or primes, respectively; and still there are questions that requires using weird pieces of math like discrete calculus to figure it out.
This specific question is phrased a little weirdly; you'd expect a "What is f(2001)?" style question to show up on an AIME-level contest (using American terms), where no proof is needed to justify your answer. In a proof-style contest, the question would generally be phrased "What are all possible values of f(2001)?", in which case a proof of uniqueness is required.
I'd be interested to see whether there's more solutions in general to this functional equation, since on first blush it seems to fall into the "Hamel basis of real numbers over rationals" trap that a lot of linear equations fall prey to, but that xy term might fix things
@@CauchyIntegralFormulaIt's true, and unfortunately, the books I've read that references those types of questions usually apply heavy substitution in their answers(in most other cases, the function is straightforward to figure out) - but there aren't any "This particular function seems to work on a certain set of numbers that the input falls into, so that's it", of course.
"I'll just sketch a proof"
Goes ahead and proves it thoroughly lol you're awesome
f(x)=x(x+1)/2
yeah i mean i kinda sketched the proof or more likely skipped it xd. I just figured out that the first values of f(x) are the integers added up to x and used teh fact that sum of the integers from 1 to 2001 is equal to (2001*(2002))/2 and got the result of 2003001.... maybe I wouldve gotten atleast some points
that's prof michael for you
Fixツ they were talking about proving the sum of the discrete differentials. It’s not a very difficult proof but Michael went ahead and basically spelled the whole thing out anyway.
It's a pretty "obvious" result, but I was wondering why that doesn't count as a proof. Now your comment leaves me wondering if that is a good proof or not. My first thought is some problem with convergence, like those operations might not be valid for cases where the sums of an do not converge.
This is the only problem in Michael's channel that I solved by myself. :)
It's been a week since I started doing one problem a day from your channel and I'd like to say that it has really helped me to think more logically (this is what Mathematics is supposed to do). Kudos to you sir.
I ended up doing it entirely recursively before watching the video. Oops 😂
In case anyone's curious, I figured out f(2) and f(1), and then used f(4) to find f(2^n) all the way up to f(1024). Then I found f(1536), f(1792), f(1920), f(1984), f(2000), and finally f(2001)=2,003,001.
This was my first instinct too! But I screwed it up badly on my first attempt, then figured out the pattern after redoing it through f(16).
Oh I did it in a similar way! But I realized I was better off finding a general form for f(nx), then I applied that to f(2000)=f(500*4) to avoid having to do too many steps in my calculations c:
@@Miju001 I did the same, way easier than the video's method
Me too
I recognized that the sum of a given number (4, for starters) has multiple arrangements.
Did f(2) + f(2) +2*2 = 10, so 2*f(2) = 6, so f(2) = 3.
Got f(1) the same way, f(3) from f(3+1), recognized triangular numbers, checked previous answers, went straight for the 2001st triangular number.
f(n+1) = f(n) + n + 1.
1: 1
2: 3
3: 6
4: 10
5: 15
6: 21
It's just equal to the triangular numbers.
The first way I thought of was to find f(2^n) up to f(1024) and down to f(1), and then just add the appropriate f values according to the binary representation of 2001.
Was also my first impulse :)
And I did it exactly like that🤦♀️
I did that too! I found
f(2ⁿ) = (2ⁿ+1) 2^(n-1)
But then I saw that by doing the substitution x = 2ⁿ we get a simple quadratic!
f(x) = (x+1) x/2
Then f(2001) is easy
f(2001) = (1001) (2001)
I really enjoy your videos, thank you so much for sharing.
New lightning setup is rad!
7:26 why not just take x=y=0?
f(0+0)=f(0)+f(0)+0*0 ...
This seems like a really long way to solve a simple problem. So I started by plugging numbers in, and like you quickly arrived at f(1) = 1, and f(0) = 0
But then i immediately went to f(n) = f((n-1) + 1) = f(n-1) + f(1) + (n - 1) * 1
f(n) = f(n-1) + 1 + (n - 1)
f(n) = f(n-1) + n
Then if you apply this recursively to f(n-1)... and all the way to f(0), it follows that f(n) is basically the sum from 1 to n.
give y=h , arrange in terms of derivatives using f(o)=0 and integrate
Could you elaborate?It seems like an interesting solution,would love to see how it works
@@arpitdas4263 if you follow his steps, you get:
(f(x+h)-f(x))/h = x + f(h)/h
now let h approach 0, the left hand side goes to f ' (x) (if it exists!) and you pretty much get:
f´(x) = lim (f(x+h)-f(x))/h as h -> 0 = x+ lim f(h)/h as h->0
so f '(x) = x+ lim f(h)/h
but lim f(h)/h as h->0 is just a constant so you can say it equals some real d.
=> f´(x) = x + d
if you then integrate, you get that f is a quadratic with leading coefficient 1/2.
using f(0)=0 you get that the constant term equals 0 and f(4)=10 yields 1/2 for the linear coefficient.
So f(x)= x^2 / 2 + x/2 =x(x+1)/2
I also did the same way
@@reeeeeplease1178 This only works if the function is differentiable, which we were not given.
@Wayne Broughton wel showing that derivative is continuous and bounded in finite interval does prove that it is differentiable func. and it can be easily shown here
I actually did this faster than Micheal! Started by f(4) = f(2+2) etc. Quickly established triangle numbers, total = 0.5n(n+1)...job done. Something to do on President's Day seeing as the market is closed!! Love the channel!!
substracting both sides by ½(x+y)², and let F(x)=f(x)-½x², we see that
F(x+y)=F(x)+F(y)
Therefore, F(nx)=nF(x) for all real x and integer n
4F(1)=F(4)=10-½(4)²=2
F(1)=½
F(n)=nF(1l
f(n)-½n²=½n
f(n)=(ⁿ⁺¹ ₂)
f can be defined by recurrence :
f(n*x) = n*f(x) + n*(n-1)*x²/2
Choose n=2001, x=1
f(2001)=2001*f(1) + 2001*2000/2
To find f(1), substitute n=2,x=1 :
f(2*1)=2*f(1) + 2*1*1/2
Same thing with n=2, x=2 :
f(2*2) = f(4) = 2*f(2) + 2*1*4/2 = 10
So f(2) = 3 and f(1) = 1
Finally f(2001) = 2001+2001*2000/2 = 2001*(1001)
Fun. Substitute g(x) = f(x) - x^2 / 2. Equation transfers into something like g(x+y) = g(x) + g(y) with g(4) = 2. The rest is trivial: g(nx) = ng(x) -> g(m/nx) = g(x) * m/n . So for rational z we have g(z) = z/4g(4) = z/2.
Yeah... For rational...
@@nemoumbra0 what’s the problem?
@@nurtasshyntas7745 our function f(x) is from reals to reals.
@@nemoumbra0 and? We need to find only f(2001). 2001 is rational.
@@nurtasshyntas7745 Ok, I just assumed you wanted to prove f(x) = x(x+1)/2 for x€R via this substitution .
Hey michael i have different approach to solve this rewrite the equation as
{f(x+y)-f(x)}/y=f(y)/y+x
Now take limits y tends to 0 .Now you will get a very familiar formula of derivative of f(x).therefore we get
f'(x)= lim y tends to 0 ,f(y)/y +x. As f(0)=0 (by checking),apply L Hopital rule on f(y)/y , you will get f'(0)=C(say).
Now our equation becomes
f'(x)=x+C, now solve by integrating both sides and using f(4)=10,you will get f(x)=(x^2+x)/2.
f'
Does lhopital rule really apply? Yes we know that f(0)=0 but we don't know that lim x->0 f(x) =0
@@FadkinsDiet f(0)=0 thats why we can apply L hopital
Got you.
@@professorpoke dhoondh hi liya
We were not told the function is differentiable, so the limit might not exist at all.
I found that f(1)=1 so therefore f(2001)=f(2000)+2001 and f(2000)=f(1999)+2000. Therefore the number must be 2001+2000+1999+1998+1997... and this is equal to 2001*1000+2001
I did essentially the same proof but without the Discrete Fundamental Theorem of Calculus:
Let x = y = 2 and simplify to f(2) = 3.
Let x = y = 1 and simplify to f(1) = 1.
Let y = 1, then f(x + 1) = f(x) + f(1) + 1*x = f(x) + (x + 1).
Let n = x + 1, then f(n) = n + f(n-1).
But then f(n) = sum {1..n} = n*(n+1)/2 for all n in N where n >= 1, using f(1) = 1 as a base case.
In particular f(2001) = 2001*2002/2 = 2001 * 1001 = 2003001.
This skips calculating f(0).
By the way it is similar to Cauchy's functional equation and it can be proved that f(x) = x * (x + 2 * f(1) - 1) / 2 for all rational x.
Yes, after finding the answer, I've proved that too. More generally, I'm wondering whether there is a theorem saying that if one has a functional equation of some form and one can prove that f(n) = P(n) for all natural numbers n, where P is some polynomial (or rational function?), then necessarily f(x) = P(x) for all rational numbers x.
@@vinc17fr You can't prove that. For Cauchy's functional equation, infinitely discontinuous solutions exist that are somewhat mental gymnastics to construct, but do exist. See p.155 of this book: www.msri.org/people/staff/levy/files/MCL/Efthimiou/100914book.pdf
@@gavinridley5727 Page 155 of this book considers irrational numbers, so that this is not a satisfactory example.
@@vinc17fr Ah yes, I misread your comment, sorry.
@@gavinridley5727 Thanks for the book!
A simpler way would be to find f(0) = 0 by replacing y with 0. Then rewrite the original functional equation as {f(x+y)-f(x)}/y = f(y)/y + x for all y unequal to 0, take limit as y tends to 0, find f'(x) = f'(0) + x, then integrate from 0 to X to find f(X) = f'(0).X + X^2/2. Plug in the given value of f(4) to find f'(0), and you have an explicit form for f(x).
I did the same way as you did
At least for whole numbers, it's the sum of all previous whole numbers. It's pretty easy to see the pattern if you break it down to f(2+2) which gives f(2)=3 and then f(1+1) which gives f(1)=1 and then both lead to f(3)=6. Which means f(2001) is 2003001
What if you differentiate this functional equation 2 times.
First by x: f’(x+y) = f’(x) + y and then by y: f’’(x+y) = 1
So f’’(x+y) = 1 which means that f(x) = x^2/2 + C*x + D
Then you can find that C=1/2 and D=0.
This solution would be much easier.
It’s not a solution tho. Derivative may not exist.
Using sum for n=1 ... N instead of n = 0 ... N, we don't need f(0) because we arrive at f(N+1) = (1+2+ .. + N) + Nf(1)+f(1). Thus f(4)=(1+2+3)+4f(1), f(1)=1, etc.
f(n)=nf(1)+n(n-1)/2, which can be proven by induction. Then get f(1)=1 from f(4)=10 and the afore given formula. f(2001) = 2001 + 2001 × 1000. One can leave it like that or go to 2001*1001 ;)
Idea of solution came to me is decomposition of 2001 in binary system.
We can easily find
f(2+2)=2*f(2)+2*2 = 10 => f(2) = 3
f(1+1)=2*f(1)+1*1 = 3 => f(1) = 1
f(2^n) = 2*f(2^{n-1}) + 2^(2*(n-1)) //closed fomula can be found for this case. But first we go the hard way...
f(2001) = f(1024) + f(977) + 1024*977
f(977) = f(512) + f(465) + 512*465
f(465) = f(256) + f(209) + 256*209
f(209) = f(128) + f(81) + 128*81
f(81) = f(64) + f(17) + 64*17
f(17) = f(16) + f(1) + 17*1
So finally we calculate all values of f(2^n) from bottom to top and then assemble value at 2001.
Too many calculations...
One more optimization is possible with relation f(x+y) = f(x) + f(y) + x*y => f(x) = f(x+y) - f(y) - x*y.
f(2001) = f(2048) - f(47) - 2001*47
f(47) = f(32) + f(15) +32*15
f(15) = f(16) - f(1) -15*1
We still have to evaluate f(2^n) = a(n).
So let us find closed form for this case.
Equation is: a(n) = 2*a(n-1) + 2^(2*(n-1)) a(n) = 2^n*b(n), a(0) = 1, b(0) = 1
b(n) = b^(n-1)+2^(n-2) => b(n) = (2^n+1)/2 => a(n) = ((2^n+1)*2^n)/2. Check: 2^(n)*(2^n+1)/2 = 2*2^(n-1)*(2^(n-1)+1)/2 + 2^(2*(n-1)).
f(15) = f(16) - f(1) - 15*1 = (16)*(16+1)/2 - 1-15 = 136 - 1 - 15 = 120
f(47) = f(32) + f(15) + 32*15 = (32)*(32+1)/2 + 120 + 480 = 1128
f(2001) = f(2048) -f(47) - 2001*47 = (2048)*(2048+1)/2 - 1128 - 2001*47 = 2003001
upd: match with Michaels answer!
This approach do not require solution of functional equation. But it may be more computationally expensive.
So I'm going to see video and check out how Michal will solve this.
upd2: Yeah. I made it hard way but it was fun. And I still think this approach might be useful in some similar tasks.
P.S. It took more time to write this because I've made mistake in relation f(2^n) = 2*f(2^{n-1}) + 2^(2*(n-1)).
Phew.
Mucho texto mierda
Ten una puta vida por favor :v
@@gabrielamartinez1079 tengo algo de respeto
You can easily find the derivative of f(x): f'(x) = lim (f(x+Δx)-f(x))/Δx = lim (((f(x) + f(Δx) + x*Δx - f(x)) / Δx) = (lim f(Δx)/Δx) + x, and if the last limit exists and equals to a, then f(x) = (1/2)*x^2 + a*x + b. By substitution f(4) = 10 and f(4+0) = f(4) + f(0) = 10 we get a = 1/2, b = 0 and f(x) = (x^2+x)/2 = x(x+1)/2. So f(2001) = 2001*2002/2 = 2001*1001.
f(x+dx) = f(x) + f(dx) + x*dx = f(x) + (df/dx)(x=0)*dx + x*dx. Integrating and using f(0) = 0 yields f(x) = (df/dx)(x=0)*x + x^2/2. From f(4)=10 we find (df/dx)(x=0) = 1/2 consequently f(x) = x/2 +x^2/2.
I had a suspicion it would be triangular numbers, but decided to solve the equation with a quadratic ax²+bx+c because by working out to f(1) i get f(x+1)=f(x)+x+1 and the +x indicates a quadratic.
Then with the quadratic 8 just input 2001 which is a very easy number because 1001*2001 isn't difficult =2003001
If you let x be arbitrary and y be a differential, you can find the derivative of f fairly quickly and find it's linear. By using x=y=0, you can find the value of f at x, then by using the initial condition you can find the derivative at 0, and you have the explicit solution!
you don't know if f is differentiable
8:44 Dat is een goede plek om te stoppen.
As a matter of fact, I have a really good friend who lives in Rotterdam. Once that covid thing is over, I should go visit him...
How's this from three weeks ago??
@@matniet43 I’m the time wizard
@@goodplacetostop2973 how do you find unlisted videos?
@@integralboi2900 Indeed. But I’m done doing this. It was funny to find that leak 2 or 3 times but now it kinda spoils the fun and the excitement of a new video. I’ll just wait, and too bad if people post the timestamp before me.
@@cyrenux Playlists
Lol personnaly i only searched for the values for 1,2,3 and 5, and observed that for odd numbers greater than 1, it looked like the statement f(2k+1) = (k+1)*(2k+1) is true. Which i prooved in a 3 lines reccurence, and so f(2001)=1001*2001.
It looks easier than all this theory haha
I solved it by using cauchy equation
f(x)=g(x)+x^2/2
By putting the value we Will get
g(x+y)=g(x)+g(y)
Hence,g(x)=ax(solution of cauchy equation)
f(x)=ax+x^2/2
a=1/2,by putting x=4
Seeing f(4)=10 is a big hint.
Once we have f(0) and f(1) the rest drops out and we know f(n) = sum(1..n). The discrete calculus is not required.
after i found f(1)=1 (using f(2)=3), I just set up a lemma saying that f(x)=f(x+1)-(x+1) and used a descending set of equalities: f(2000)=f(2001)-2001, f(1999)=f(2000)-2000... f(4)=f(5)-5, and summed them all up, giving f(4)=f(2001)-2001-2000-...-5=f(2001)-2002991=10, and so f(2001)=2003001
There is alternative way to directly find f(x), by converting this to a differential equation. Simply put y=Delta x, rearrange to obtain (f(x+Delta x)-f(x))/(Delta x)=f(Delta x)/(Delta x)+x, take the limit as Delta x->0, show L hopital applies to the RHS, and you find:
f(x)=(x+x^2)/2
I just realized this, you beat me to it!
check 5 posts before yours :)
If the function is not differentiable the limit might not exist.
@@Notthatkindofdr That's OK: I simply sought a differentiable solution to the presented problem, and succeeded. On that note, I spent some time trying to prove that solutions to this functional equation are at a minimum continuous. If you have any insight on whether it's possible to prove continuity of f(x) here, I'm really curious to hear. I found that if f(x) is continuous about x=0, then f(x) is differentiable everywhere, but can't show continuity at the origin. I think maybe this functional equation admits infinitely discontinuous solutions like in this book:
www.msri.org/people/staff/levy/files/MCL/Efthimiou/100914book.pdf
@@gavinridley5727 I haven't looked at that link, but there are infinitely many discontinuous solutions. As someone else observed in the comments, if you let g(x)=f(x)-x^2/2, then g(x) satisfies Cauchy's functional equation (and vice versa), and as observed on the Wikipedia page en.wikipedia.org/wiki/Cauchy's_functional_equation there are infinitely many solutions.
My solution, with no difference operator:
General approach: Express f(2001) as f(2000+1)=f(2000)+f(1)+2000
A) Finding f(2000):
Break down by reducing argument by 4 repeatedly:
f(2000)=f(4)+f(1996)+(4)(1996), f(1996)=f(4)+f(1992) +(4)(1992), f(1992)= ... f(8)=f(4)+f(4)+(4)(4)
By inspection, we have 500 terms of f(4), and 499 terms (4)(4n)
f(2000)=(500)(10)+(16)(Sum of first 499 natural numbers)
=500(10)+16(499)(500)/2
=2,001,000
B) Finding f(1):
I used the same approach as Michael, finding first f(2)=3 and then f(1)=1
=>f(2001)=2,001,000+2000+1
=2,003,001
It’s funny, I think we could’ve used the discrete fundamental theorem of calculus to solve the question from yesterday’s video.
Usually the fundamental theorem of calculus is written using capital F for the antiderivative. Now the function and the antiderivative are both written with the same symbol f. But I think here everyone understands it anyway.
He wrote f for the antiderivative of df/dx.
2001=1997+4, which allows to write f(2001)=f(1997)+f(4)+4*1997, and below f(1997)=f(1993)+f(4)+4*1993 and so on, until one finds f(1)=f(1)+f(0) +0,so f(0)=0. By adding all the lines one gets the result.
f(4) = 10 = f(2+2) = 2.f(2) + 4 => f(2) = 3
f(2) = 3 = f(1+1) = 2.f(1) + 1 => f(2) = 1
given the value of f(4), you can easily work out f(8)=f(4+4), f(16)=f(8) etc. all the way to f(1024)
2001 = 1024+512+256+128+64+16+1
If you set x=y=0, f(0)=0. Then, set x=1 and y=0, and you get f(1)=1. Move forward and set x=1 and y=1, and then f(2) is obviously equal to 3. Going on, f(3)=6 and, setting x=3 and y=1, f(4) becomes 10. Do we even need the statement f(4)=10 beforehand? I might be missing something... It seems like f(n+1)=f(n)+(n+1), so f(n+1)=f(0)+1+2+...+n+(n+1)=f(0)+(n+1)(n+2)/2. Then, for n=2000 we can see pretty straight-forwardly that f(2001)=2001(2002)/2, which is the same result as Michael gets.
"Then, set x=1 and y=0, and you get f(1)=1." No, you get f(1+0) = f(1) + f(0) + 1x0, i.e., f(1) = f(1). The condition f(4)=10 is what allows one to determine the value of f(1).
If you try with some simple polynomial guesses (e.g. linear, quadratic,...) you quickly see that the function is f(x)=x(x+1)/2 for all real numbers. In my experience, a significant percentage of such problems is solved with simple functions, so it is worth a try.
F(x) =1/2x^2+1/2x
Thanks to those pointing out the Cauchy's functional equation. I tried to prove that f(x) is exactly x^2/2, so the conditions are wrong, and failed, though it's a good warm-up :)
I solved the Problem by finding a recursive formula of f(mx) = mf(x) + ((m-1)m/2)square(x).
Since f(4)=10 then f(4) = 4f(1) + 6 implying f(1)=1
And then calculate f(2001)
Nice video. FYI: In your last few videos the camera auto-focus is sometimes misbehaving.
He noted this in the last one. I suspect it’s because with a clean board, there aren’t really any sharp lines of contrast at the focus spot to fix on (which is usually how autofocus works-find a line and make it as sharp as possible), so it goes hunting. Just setting an autofocus point before filming and then locking in manual focus might be a good strategy.
@@PaulFisher Agreed, the focus should be fixed, as Michael stays in one plane (more or less). He does not wander towards and away from the camera.
I just proved by induction a multiplicative property of this function. Worked out pretty well. I will keep this problem in mind for the hommies.
Such a nice solution~
TY
If this is an objective type question in some exam. The best approach is to assume that f is differentiable. We will get the answer.
since f(x+y) = f(x) + f(y) + xy and f(4) = 10,
let x = y = 2
f(2+2) = f(2) + f(2) + 2*2
10 = 2 * f(2) + 4
f(2) = 3
then repeat with x = y = 1
f(2) = 2f(1) + 1
f(1) = 1
and now y = 1
f(x+1) = f(x) + f(1) + x
f(x+1) = f(x) + x + 1
or f(x) = f(x-1) + x
This means that for any x>=1 f(x) equals the sum of all natural numbers from 1 to x.
The average value of such a number is (1+2+...+(x-1)+x)/x. From here we can always pair up the first with the last element of the sum, then the second with the last but one element, and so on.
So we get (1+x)*(x/2)/x = (1+x)*x/2
f(x) = (x^2+x)/2
This video is listed in OEIS sequence A000217.
I ended up doing the problem by computing f(2^n) manually up to f(2048). Then using this it was not hard to show the value of f(2000). Finally finding the value of f(1) I used that that f(2001)=f(2000)+f(1)+2000 which solves the problem
8:26 He has 1000 * 2001 + 2001 and instead of just evaluating it (put three zeroes behind the 2001 because you are multiplying it by 1k and then add 2001 to that number) he makes it into something more complicated 4head
Can you do a video series on FUNCTIONAL ANALYSIS
more general in Korean Math exams and questions method:
x=y=0 then we know f(0) = 2f(0)+0 so f(0) = 0, then lim0> f(h)/h = f'(0)
think about f'(x), we know f'(x) = lim0> {f(x+h)-f(x)}/h = lim0> {f(x)+f(h)+xh-f(x)}/h = lim0> {f(h)+xh}/h = f'(0)+x
so f'(x) = f'(0)+x, and also f(0)=0 so f(x) = (1/2)x^2 + f'(0)x
when x=4, f(4) = 4f'(0)+8 = 10 so f'(0) = 1/2
Finally we know that f(x)= (1/2)x^2 + (1/2)x = (1/2)x(x+1)
x=2001 -> f(2001) = (1/2)*2001*2002 = 2001*1001
10 = f(4) = f(2)+f(2)+4, so f(2) = 3.
3 = f(2) = f(1)+f(1)+1, so f(1) = 1.
f(n+1) = f(n)+f(1)+n, but f(1) = 1, so f(n+1) = f(n)+(n+1).
Should be obvious now that f(n) is adding all numbers from 1 to n, i.e. triangular numbers.
Past me is smart
I guessed that f(x) is quadratic
This xy summand suggested me that f(x) might be a quadratic
From binomial expansion I know that (x+y)^2=x^2+2xy+y^2
so f(x)=ax^2+bx+c is a good guess
The attempt of an engineering student:
f(x+y) = f(x) + f(y) + xy (eq 1)
My first thought f(x) = x^2, but that would be 2xy, and I don't really see a way to progress from there.
Instead I'm trying differentiation: Derivating in x in both sides we get: f'(x + y) = f'(x) + 0 + y. Now that is a very interesting result isn't it? I think that means f'(x) is a linear _(affine actually, everybody says linear for wtv reason I haven't understood why the 2 terms are confused!)_ function with slope 1. So f'(x) = a + x. Through indefinite integration/primitivation (I don't remember the correct term! D: ) we know f(x) = b + ax + (1/2)x^2. Plugging this back in eq 1
b + a(x+y) + (1/2)(x^2+2xy+y^2) = 2b + a(x+y) +(1/2)(x^2 + y^2) + xy
0 = b
so now only a is left to determine! Which we of course can do with the extra (boundary perhaps would be a better term?) condition given: f(4) = 10 a4 + (1/2)4^2 = 10 a = 1/2
and f(x) = (x+x^2)/2, so f(2001) = 2 003 001 ? (calculator helped :p)
Going back to the idea of advantage of the "close but not right" result with f(x) = x^2 where the "non-linear extra" ( f(x+y) - f(x) - f(y) ) was wrong by a factor of 2 (it is 2xy instead of xy). One could think to to divide the function by 2 then? I'm not sure if that makes sense in a rigorous way, but intuitively it makes some sense haha one would then try f(x) = (1/2)x^2 which gives f(x+y) = f(x) + f(y) + xy ! Now if I had gotten here the first time it I bet I would had confused me and would had taken a while to realize that this is not the ONLY solution, thinking I must have done something wrong as f(x) = (1/2)x^2 solves eq 1 but doesn't respect f(4) = 10
Luckily, one can realize that if f respects eq 1 then f + g, where g is any linear function, also respects eq 1, then one would simply have to realize that (1/2)4^2 = 8, and we want it to equal 10, we need to add 2. So we need to add a linear equation that is 2 when x is 4, so we need to add (1/2)x.
This second way is probably the "smarter" way to do it. The way I did it although is a good reminder on how the correct usage of mathematical tools is a great replacement for intelligence haha
I'll watch the video now, thanks for the puzzle :D
Edit: wow, after watching the video, I have to say it's such a reminder of how mathematicians think differently to engineers. Silly me assuming the function would be differentiable, and silly me just looking for "the" solution, instead of looking for all possible solutions hahah
Did it all so to say 'on foot'. Calculated f(2), f(1) and all of them to f(512), then f(667) using the previous ones, then just calculated f(2*667 + 667)
I really enjoyed this problem, and I managed to prove that for any rational number r and any real number x we have f(r⋅x) = r(r-1)/2⋅x² + r⋅f(x). In particular, with x=1 and f(1)=1, for any rational number r we have f(r) = r(r+1)/2.
My question now is, can we extend the result f(x) = x(x+1)/2 for every real number x, without assuming first that f is continuous? In particular, can it exist non-continuous functions where for instance f(sqrt(2)) is not equal to sqrt(2)⋅(sqrt(2)+1)/2 i.e. 1+1/sqrt(2)?
The following comment, by @Samuraiwarm, answers your question:
"Let f(x) = g(x) + x^2/2, we get
g(x+y) + (x+y)^2/2 = g(x) + x^2/2 + g(y) + y^2/2 + xy
The polynomial of x,y all cancels out and we get g(x+y) = g(x) + g(y), which is a Cauchy's functional equation. Even though there exists exactly one solution of f over rational numbers, there are infinite number of solutions over real numbers."
@@ricardocavalcanti3343 I can't find the comment by @Samuraiwarm but you are right, it completely answers my question. Better that that, I discovered this notion of Cauchy's functional equation that I never heard of. Thank you very much for it!
I do it in another way. From the value of f(1), f(2), f(3) and f(4), I summarize f(x)=f(x-1)+x. Then subtract both sides by f(x-1). After that, add the summation from 2 to 2001. And find the value exactly the same.hh
using f(x) = f(x-1) + x, and the fact that f(1)=1, I figured out that it is just summing up all the natural numbers till x, and therefore f(x) is the xth triangular number. So f(2001) = 2001*1001
In the way the question is, it's clear there is only one solution so just try polynomial of degree 2 give quickly the result.
I did not initially realize that we only needed to find f(2001) - it is pretty straightforward to show that f(n+1)-f(n)= n+1 and calculate the result from that. I found it pretty interesting to prove that the only real function was f(x) = 1/2 (x)(x+1) by showing that 1/delta_x (f(x+delta_x)-f(x)) = x + 1/2 - you need to prove that lim(x to 0) f(x)/x = 1/2 (which you can show by proving that f(nx) = nf(x) + (1/2)(n)(n-1)x )
We were not told the function is differentiable, and if not then your solution would not apply (the limit might not exist).
That's not the only real function --- it's the only *continuous* real function. See the comment by @Samuraiwarm.
@@ricardocavalcanti3343 I don't see any comment by @Samuraiwarm
@@dneary Here is his comment:
"Let f(x) = g(x) + x^2/2, we get
g(x+y) + (x+y)^2/2 = g(x) + x^2/2 + g(y) + y^2/2 + xy
The polynomial of x,y all cancels out and we get g(x+y) = g(x) + g(y), which is a Cauchy's functional equation. Even though there exists exactly one solution of f over rational numbers, there are infinite number of solutions over real numbers."
You can find more details in en.wikipedia.org/wiki/Cauchy%27s_functional_equation.
@@ricardocavalcanti3343 Thanks. Indeed, that is very cute... Defining f(x) to be some arbitrary number as part of an infinite basis for reals is... a bit twisted. It certainly looks like it should be continuous at first glance!
My approach was to
find the deriv:
f(x+dx) = f(x) + f(dx) +x*dx => f’(x) = f’(0)+x => f(x) = x*f’(0) + (x^2)/2 +C
f(0) = 0 , f(4)=10 => f(x)=(x+x^2)/2
Are you from india?
@@BCS-IshtiyakAhmadKhan Umm... no, Los Angeles. Were you so amazed by my math skills you thought I must be Indian? :-)
We were not told the function was differentiable.
@@Notthatkindofdr I proved it was differentiable, by finding the derivative.
@@jbtechcon7434 No, because you assumed that the limit of f(h)/h as h->0 existed. It might not.
As a high school student, i dont really get it but i sure was amazed, awesome video.
Once you find f(1) the problem will become so easy
f(2001) = f(2000) + f(1) + 2000
f(2001) = f(2000) + 2001
f(2000) = f(1999) + 2000
.
.
f(2) = f(1) + 2
f(1) = 1
By adding all the equations we will simply get
f(2001) = 1+2+3+.....+2001
Which is (2001/2)(2001+1) which is the same result.
What you're calling the "Discrete Fundamental Theorem of Calculus" is basically how I describe the regular "Fundamental Theorem of Calculus" to students. I use a picture too. :-)
Try finding f(1/3).
Oh sh*t, I'm Dutch (at least my origins are) and this one is mine I thought. And guess what, I was right. Plug in a quadratic expression for f(x) - it really begs for it - and equating coefficients, together with the condition on f(4) the function rolls out naturally and within seconds, or tens of seconds. The rest is trivial.
Keep up your good and brilliant work Michael ! :-)
Thats what I did, but it's not rigorous. It doesn't prove that this is the only solution. But yes when you see x+y transform into xy you should be thinking about squaring it.
I followed everything until you turned f(4) into 2f(2)+4. Can someone explain?
Put x=y=2 on both sides
I tackled this using f(2001)=f(4)+f(1997)+4x1997. Repeat for f(1997) and so forth until f(2001)=500xf(4)+4x(1997+1993+...+1)+f(1). We know f(4) is ten, just need to solve for f(1) and that large sum.
i wrote the results for f(x) from 1 to 5 on the side and noticed its just the sum of every number from 0 to n... and then i tried to do a sum from 0 to 2001...and got 1553001, because i forgot to add (45 * 10000)....
Lesson: just learn to add correctly OR look up a formula...
Please make a video for 1001*2001
I first found f(0), f(1), f(2) and f(3). Then I used induction to prove that f(n) = n(n+1)/2 for integer n.
I did it quite in the same way. First of all I found the value of f(1) and then I noticed that:
f(x + y) = f(x) + f(y) + xy => f(x + 1) = f(x) + x + 1
f(x + 1) = f(x) + x + 1
f(x) = f(x - 1) + x
f(x - 1) = f(x - 2) + x - 1
.
.
.
f(k) = f(k - 1) + k
now we set x = 2000 and k = 5 and add all these equations to get the following:
f(2001) = f(4) + 5 + 6 + ... + 2001 => f(2001) = 2003001
Guess it's a quadratic, solution f=(x^2+x)/2
Hum, there was a -xy at the begining then a +xy later. So I did the problem with the wrong thing !!
I found the values of f(1),f(2),f(3) then I saw a pattern where f(x+y)=(x+y)(x+y+1)/2
Soooo I prove that and then use that fact to reach to 2001*1001
Leaving this video off with a standard calculation instead of just doing the multiplication is a bit like ending a song on a half cadence and I feel very unsatisfied.
I think leaving it like this is a cleaner way of representing the number.
This test was for HS mostly. I believe that HS students haven’t been taught the Fundamental Theorem of Calculus. So is there another approach?
Yup. It is pretty easy to find the values of f(2) and f(1) from the given info. These come out to be 3 and 1 respectively.
Now, f(x+1) = f(x) + f(1) + 1.x
f(x+1) = f(x) + (x+1)
Or to put it better, f(x)= f(x-1) + x
Now, using this fact and the fact that f(1)=1, we notice that f(x) will give us the sum of the first x consecutive natural numbers, which is x(x+1)/2 [standard result]
Substituting 2001 for x, we get 2001×1001
The flag in the thumbnail image is French, not Dutch.
It's Dutch. It's just tilted sideways.
I like the sound of your chalkboard.
Do f((1+1)+(1+1)) to calculate f(1)
Easy problem... solved it in less than 30 seconds
How did you do that in less than 30 seconds it takes at least a min.
@@rajbunsha8834 I can explain my working;
Since we know that f(x+y)=f(x)+f(y)+xy, and f(4)=10, we can substitute 4 as 2+2.
f(4)=10
f(2+2)=10
f(2)+f(2)+2•2=10
2•f(2)+4=10
2•f(2)=6
f(2)=3
Now using the same method, f(2)=f(1+1)
f(1+1)=f(1)+f(1)+1•1
3=2•f(1)+1
2=2•f(1)
f(1)=1
Now writing f(4) as f(1+3), we get f(3)=6.
We see a pattern between the values at different steps and we can find f(5) to be 15.
To sum up the pattern,
f(1)=1
f(2)=3
f(3)=6
f(4)=10
f(5)=15
We can safely conclude that the function is simply the sum of ‘n’ consecutive natural numbers and thus f(2001)=2001*2002/2
@@rajbunsha8834 I did this calculation in my head very quickly 😅
Same
@@arjunchawla2248 I did the same thing as @Arjun Chawla
•Taking x=y gives f(x+x)=f(x)+f(x)+x*x
=>f(2x)=2*f(x)+x^2 ---(1)
Notice we have an initial condition of the form f(2^n). Using this we can figure out f(1) like how @Arjun Chawla did. Then we notice we can apply (1) recursively. Since we have f(x) (obviously) and f(2x), now we can figure out f(3x) and then f(4x) using f(3x) and f(x) and so on. And look, this gives f(nx) for natural n where we can take n=2001 to get what we want. This is where f(1) comes in because f(nx) is n*f(x)+ x^2* n(n-1)/2
Taking x=1 gives f(2001)=2001*f(1)+1^2* 2001(2000)/2=2001*2002/2=2001*1001
i like this kind of overkill because it requires minimal creativity and guessing to correctly solve a problem. there are plenty of places to learn creative or guessy solutions to problems, such as testing the values f(1) through f(5) and guessing "it's just x(x+1)/2" to get the answer, but this irons out the exact answer without any such guesswork
I solved it in easier and faster way for any x, i.e., finding f(x)
Step 1:
y=0 => f(x)=f(x)+f(0) => f(0)=0
Step 2:
We assume f is continuous and f’=df/dx exists
We differentiate on both sides of the equation over x with y being parameter independent of x (i.e., partial differentiation sigma f(x,y)/sigma x, y being free number)
=> d[f(x+y)]/dx = d[f(x)+f(y)+xy]/dx
=> f’(x+y)=f’(x)+y, with f’=df/dx and y is free number independent of x.
We set x=a and z=a+y (x is fixed to a)
=> f’(z)= f’(a)+z-a, z reel number
=> f’(z)= z+A, with A=f’(a)-a
=> f(z)=1/2*z^2 +Az + b
Since f(0)=0 => b=0
f(4)=10 => 1/2*16 + A*4=10
=> A=1/2
=> f(z)=1/2*z^2 + 1/2*z
=> f(z)=z*(z+1)/2
And
f(2001)=2001*1001
Note that we assumed f is continuous and f’ exists at the beginning and the result for f did not contradict our assumption, thus the assumption was correct and the solution for f exists as a continuous function.
Was my method really that bad that you had to delete it or did my original comment just not pass through?
Sometimes RUclips doesn't save a comment. It happens to me often.
f(n) is just n th triangle number man!!!
No one's going to talk about the French flag-looking Dutch flag? No? How about the Hungarian flag from the Italian flag?
Dutch flag is 200 years older than the rotated French flag.
Also, the Dutch flag has the distinct advantage to be wearing out gracefully until the flag pole, while the French flag loses its “rouge” when it has unraveled for 1/3.
Of course, and the Dutch flag turned 90° gives the French one... I admit that was the reason I watched this video :)
(2001^2)/2
Do a problem from the bulgarian math olympiad, there are very interesting ones😁
I still miss the backflip.
It's the only problem I've been able to do on my own with just my phone's notepad.
I did it by two different ways. I thought "Well, we don't know f(2001), but we can remove 4 from it", and got f(2001)=f(4)+f(1997)+4*1997. Obviously, I didn't know f(1997) either, but we got progress. So I got f(2001)= 500*f(4) + f(1) + (sum of 4*(2001-4k) as k goes from 1 to 500).
Obviously I didn't know f(1), but I knew the sum was equal to 1,998,000, so the answer was 2003000 + whatever f(1) is.
So now I have to find f(1). I figure "fine, I'll just do the opposite, make it so I find things that add to 4 and use that". So I got f(4) = 2 f(2) + 4, so f(2) = 3.
f(4) = f(1) + f(3) + 3, so f(1) + f(3) = 7
and finally f(3) = f(1) + f(2) + 2, so f(3) = f(1)+5.
In hindsight, I could have used f(2) = f(1+1) = 2f(1)+1, but I decided to go the long route and find that f(1) = 1 and f(3)=6. So I finally found that f(2001) was equal to 2003001.
But by then I thought "Hey, wait a second, 1-3-6-10, that's the triangular numbers !", and then I realized that f(x+1) = f(x)+f(1)+x, or f(x+1)=f(x)+x+1 ! My dumb brain didn't see the obvious sum, only that x had to be quadratic because the difference is linear, but it's actually easier than what I did.
Since f(x+0) = f(x)+f(0), we have to have f(0)=0, so f(x) is the sum of all natural numbers before x, which is equal to n(n+1)/2.
In even more hindsight, it's pretty obvious that the functional equation is one for the sum of all natural numbers. the sum of all numbers from 1 to x+y is the sum from 1 to x plus the sum from x to x+y. We can remove x from each one since they're greater than x, so we remove xy, and we're left with 1, 2, 3, 4... up to y. So f(x+y) = f(x) + xy + f(y).
Can u assume y is close to 0 then change it from f(x+h)=f(x)+f(h)+xh to f'(x)=x+f'(0) then solve the equation??
You don't know that f is differentiable.
I forgot :L. I feel stupid
probably the only question I can answer in this channel lol
Ho sbagliato perché x----->(x/rad2) ^2 soddisfa solo la prima condizione
Ans:- 2003001!!! 😁😁👍👍
If you start the summation at n=1, you don't even need f(0).