A Nice Rational Equation from Crux Mathematicorum
HTML-код
- Опубликовано: 7 фев 2025
- 🤩 Hello everyone, I'm very excited to bring you a new channel (aplusbi)
Enjoy...and thank you for your support!!! 🧡🥰🎉🥳🧡
/ @sybermathshorts
/ @aplusbi
❤️ ❤️ ❤️ My Amazon Store: www.amazon.com...
When you purchase something from here, I will make a small percentage of commission that helps me continue making videos for you.
If you are preparing for Math Competitions and Math Olympiads, then this is the page for you!
CHECK IT OUT!!! ❤️ ❤️ ❤️
❤️ A Differential Equation | The Result Will Surprise You! • A Differential Equatio...
❤️ Crux Mathematicorum: cms.math.ca/pu...
❤️ A Problem From ARML-NYSML Math Contests: • A Problem From ARML-NY...
❤️ LOGARITHMIC/RADICAL EQUATION: • LOGARITHMIC/RADICAL EQ...
❤️ Finding cos36·cos72 | A Nice Trick: • Finding cos36·cos72 | ...
⭐ ⭐ Can We Find The Inverse of f(x) = x^x? • Can We Find The Invers...
⭐ Join this channel to get access to perks:→ bit.ly/3cBgfR1
My merch → teespring.com/...
Follow me → / sybermath
Subscribe → www.youtube.co...
⭐ Suggest → forms.gle/A5bG...
If you need to post a picture of your solution or idea:
in...
#radicals #radicalequations #algebra #calculus #differentialequations #polynomials #prealgebra #polynomialequations #numbertheory #diophantineequations #comparingnumbers #trigonometry #trigonometricequations #complexnumbers #math #mathcompetition #olympiad #matholympiad #mathematics #sybermath #aplusbi #shortsofsyber #iit #iitjee #iitjeepreparation #iitjeemaths #exponentialequations #exponents #exponential #exponent #systemsofequations #systems
#functionalequations #functions #function #maths #counting #sequencesandseries
#algebra #numbertheory #geometry #calculus #counting #mathcontests #mathcompetitions
via @RUclips @Apple @Desmos @NotabilityApp @googledocs @canva
PLAYLISTS 🎵 :
Number Theory Problems: • Number Theory Problems
Challenging Math Problems: • Challenging Math Problems
Trigonometry Problems: • Trigonometry Problems
Diophantine Equations and Systems: • Diophantine Equations ...
Calculus: • Calculus
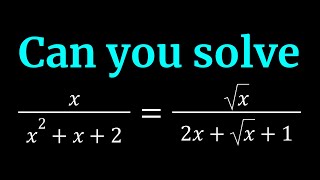








This was fun to solve. My aha moment was seeing that I could add 12x and make a perfect fourth power. Then it turned nicely into two similar quadratics which were not fun to solve.
indeed a very nice problem
Nice!
At 7:52 when you want to solve the quartic equation
x⁴ − 4x³ − 6x² − 4x + 1 = 0
you should _not_ start by depressing this equation, since this will only complicate things and is redundant when using Ferrari's method for solving quartic equations. First we bring all terms of a lower than the third degree over to the right hand side, which gives
x⁴ − 4x³ = 6x² + 4x − 1
Observe that at the left hand side we have x⁴ = (x²)² and 4x³ = 2·(x²)·(2x) so we can complete the square at the left hand side by adding (2x)² = 4x² to both sides since (x²)² − 2·(x²)·(2x) + (2x)² = (x² − 2x)². So, adding 4x² to both sides we get
(x² − 2x)² = 10x² + 4x − 1
Now, if we take any number k and add 2k(x² − 2x) + k² = 2kx² − 4kx + k² to both sides, then the left hand side will _remain_ a perfect square regardless of the value of k, because at the left hand side we then have (x² − 2x)² + 2·(x² − 2x)·k + k² = (x² − 2x + k)². So, adding 2k(x² − 2x) + k² = 2kx² − 4kx + k² to both sides we get
(x² − 2x + k)² = (10 + 2k)x² + (4 − 4k)x + (k² − 1)
Since the left hand side remains a perfect square regardless of the value of k, we are now free to select a value of k that will make the right hand side a perfect square as well. However, there is no need to calculate the discriminant of the quadratic in x at the right hand side and set this discriminant equal to zero and then solve the resulting cubic equation in k. It is easy to see that for k = 1 both the linear term (4 − 4k)x and the constant term (k² − 1) vanish, leaving only the quadratic term (10 + 2k)x² which equals 12x² for k = 1. So, with k = 1 we get
(x² − 2x + 1)² = 12x²
and since x² − 2x + 1 = (x − 1)² this can be written as
(x − 1)⁴ = 12x²
which is of course exactly the equation you obtained at 5:14.
Wow! This is pretty good. Thanks for sharing 😍
@@SyberMath Also note that when you depressed the quartic by substituting x = y + 1 you obtained
y⁴ = 12y² + 24y + 12
at 8:18 after bringing over all terms of a lower than the third degree to the right hand side. You then claim that adding 2ky² + k² to both sides didn't give you anything nice. Really?
Take a closer look at the right hand side of your equation in y. If we take out the common factor 12 we have
y⁴ = 12(y² + 2y + 1)
or
y⁴ = 12(y + 1)²
So, the right hand side actually _already is a perfect square_ and there is therefore no need to add anything to both sides to make the right hand side into a perfect square. Also note that if we back substitute y = x − 1 in this equation we get (x − 1)⁴ = 12x² which is exactly the equation obtained by applying Ferrari's method to the original quartic in x.
But let's suppose we don't notice that the right hand side of y⁴ = 12y² + 24y + 12 already is a perfect square and proceed by adding 2ky² + k² to both sides of the equation in y, then we obtain
(y² + k)² = (2k + 12)y² + 24y + (k² + 12)
The quadratic in y at the right hand side will be a perfect square, that is, the square of a linear polynomial in y, if and only if its discriminant is zero, which is the case if and only if k satisfies
24² − 4(2k + 12)(k² + 12) = 0
which reduces to
k³ + 6k² + 12k = 0
Do you see what I see? This cubic equation in k has no constant term, so k = 0 is a solution. This makes perfect sense, because, as we already saw, the right hand side 12y² + 24y + 12 already is a perfect square, so there is no need to add anything to both sides. Of course, adding 2ky² + k² to both sides with k = 0 amounts to adding nothing at all to both sides.
k=0, since 12y^2+24y+12 = (2 sqrt(3) (y+1))^2
That's great. I didn't have a clue about this one, and you made it easy - method 2.
Glad to hear that!
After noting that 1 is not a solution to the equation, we can put x=y+1/y-1 and get the quadratic equation 3y⁴-6y²-1=0. By solving this equation with the unknown y, we deduce the solutions to the equation with the unknown x.