Geometric Algebra Applications - Kepler Problem (Part 1)
HTML-код
- Опубликовано: 5 фев 2025
- In this video, we will begin our study of the Kepler problem, in which two masses move under an inverse-square law, namely the law of universal gravitation. We will derive the equation that needs to be solved and also talk about two conservation laws: angular momentum (geometric algebra perspective) and the conservation of energy.
References / Further Reading:
1. adsabs.harvard....
2. Lasenby and Doran's "Geometric Algebra for Physicists"
3. en.wikipedia.o...
4. en.wikipedia.o...
5. en.wikipedia.o...
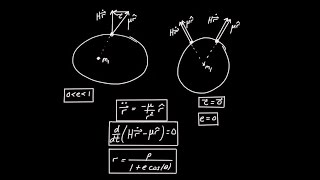

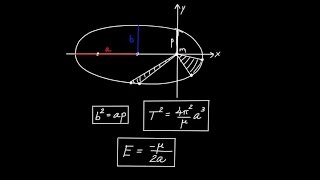






Geometric algebra works so great in illustrating conservation laws, nice
Another way to that the dot product between r^ and r^\dot is zero: r^ by definition cannot change along the r^ direction. If it did then its length would change and it would no longer be a unit vector. Therefore it can only change in the perpendicular direction (ie a rotation). [This is like uniform circular motion where an object's acceleration (v\dot) is perpendicular to its velocity (v)]. If r^ and r^\dot are perpendicular then their dot product must be zero!
what's "r^"?
@@NoNameAtAll2 \hat{r} in MathJax, or r-hat in literate English; the unit vector oriented the same way as vector r.
13:00 kind of confused me because we were treating that wedge product as a scalar even though it has that e1e2 unit, but i think i understand it now. that unit is literally base x height, so it just means that the wedge product IS an area, and not just the magnitude of a wedge product is an area
Yep although it is the area can be negative depending on which order the wedge product is in
Base and height are scalars. e1 and e2 are vectors. I think the presentation was messed up.
Interesting presentation. Although I think there is a hidden assumption, that mas m1 is much greater than m2, so it does not move. The position vector r is defined as the position of mass m2 with respect to m1. In the video is assumed that both masses are accelerated, with opposite direction. However, this means that the position vector r is defined in a non inertial reference system. Therefore, Newton's law has to be corrected with inertia forces. If m1 >> m2 ( as it is the case with the Sun and the Earth, for example) you can neglect the motion of mass m1 and the reference system is inertial. In the general case of two masses of similar mass you have to choose as origin of the reference system the center of mass of both masses. If the two masses are isolated, the center of mass does not move, and this reference system is inertial,
Just a quick note / question at time 26:18 : When you define the vector r (r bar) you say that it's equal to a constant, r, times r^ (r hat). But r is not a constant as it varies with time (because r bar varies) and if it was a constant the derivative would be zero and not °r (r dot). Can you confirm that little r is not a constant but a magnitude that varies with time. Thank you for very interesting lectures very clearly presented.
I think he had just misspelled it.
He should have said scalar insted of constant.
what i always like to do with that 4:10 is use Gmr/|r|^3 since the norm of the vector is v/|v|
excellent presentation.
7:30 Angular momentum.
At 22:14 you say that using the chain rule R dot comes in front... if we forget the constant u the only thing we're left with is 1 over r and the derivative of 1/r is -1/r^2, can you please explain me where r dot comes from ? I love your videos Thanks
Germain Guerin Chain rule
@@yusufakn7173 yes that's what he says and i know the chain rule but i don't see how it comes here, can you show me please
You should take derivative with respect to t instead of r
@@yusufakn7173 ok, last attempt, can you show me please what is the inner function and the outer function as g(h(x))'. Thanks for taking the time to answer me.
d(m/r(t))/dt=md(1/r(t))/dt=md(1/r)/dr*dr/dt=m(-1/r^2)r(dot) m is for mu
how is this different from old vector algebra
It seems slightly faster than the usual derivation. I'll have to compare it later in my notes.
Thanks for taking the time to produce the mathematics with the graphic geometric depictions of the concepts. That really helps me to understand what is happening in the mathematics! I tend to think very geometrically at least up to 5 dimensions after that things start to get really fuzzy.
I've uploaded some resources on using GA to calculate an orbit. The links are in the description of the video *How Can the Atmosphere Rotate with the Earth?* (v=5E57Eg7rmOE)
I don't get how r1.. is an acceleration acting on an object, but it's also the second derivate of an arbitrarily chosen vector. Shouldn't they at least have the same direction?
+mrBorkD
No the acceleration r1.. need not be in the same direction as r1.
Mathoma That makes sense.
I still don't get it though :(
+mrBorkD
Which part are you not grasping? Perhaps drawing out the vectors as m1 moves over small time increments may help.
The acceleration goes in the same direction as the force, and the force comes from the other body pulling in the centre of the orbit. The acceleration vector points to the centre of the orbit.
This is so satisfying
beautiful
+Mi Les
Thanks! We'll get into the conic section stuff in the next video, which should be out in the next couple days.
Stunningly, Pythagoras would appreciate post murder
great video
In a world without GA, the approach to doing this problem might have used cartesian coordinates in 2D and then generalized in 3D. In others of his videos, the cartesian system features throughout in terms of the base unit vectors e1,e2,e3. This video doesn’t use a cartesian frame of reference, only a point in space. There are displacement vectors r1 and r2. Masses m1 and m2. I was intrigued by the claim that the acceleration of vector r1 was equal to the gravitational force of m2 acting on m1 divided by the mass of m1. This is newton’s law but the direction of vector r1 and the direction of acceleration(vector) of r1(double dot) are not the same! Yet they were equated after division by m1 which is a scalar mass! This troubled me from the beginning. Is this saying that vector qualities having both magnitude and direction can be equal in a GA world even though their directions are not the same! Or is there a problem in semantics and meaning of terms.? Then the application of the product rule in differentiation across dot or wedge products! This is more believable because these operators can be viewed as functions. But the results were correct. This demonstrates to me how wedded I am to a cartesian approach. But a GA approach that doesn’t do enough house keeping is going to be hard to follow.
Replying to my own comment.
Or is this saying that differentiation transforms displacement vector r1 into a new (acceleration)vector r1 in the direction of F12. But I see now that the heading to this video gives references to look up.
What I should have said is that double differentiation of the displacement vector r1 transforms it into a new vector of acceleration and this according to Newton's Law, must be in the direction of F12.
The thing to note here is that the force of gravity is central, and conserved. Which is to say that the force per mass (or the total energy of the system) is equal and opposite, but the affect on the momentum is the reciprocal of the mass. This is most evident in this 2-body system.
When it comes to the lack of coordinates in GA, it's true as well in other vector algebras, it doesn't matter until you want to actually talk about absolute magnitudes. Things of physical interest tend towards multiplication or exponentiation, even things like rotations, as seen with the use of Euler's formula for rotations. This is very nice.
15:40 isn't the product rr^ a scalar by a vector? why do you apply the derivative of a product like the scalar is a variable? Am I missing something? You eliminate the derivative-of-constant part with the wedge product later, and it doesn't change much tough
The distance between the masses can change (e.g. in an ellipse). Therefore its a variable. Its easy to check a scalar and a vector obey the product rule:
d/dt(av_1,av_2,av_3)=(ad/dtv_1+v_1d/dta,...
I wont write everything since its hard to write math in a youtube comment
@@David-km2ie download scientific keyboard
Ρ(∂v/∂t + (v•∇)v) = -∇p + ρg + μ∇²v
f * g = ∫₀ᵗ f(t)g(t - τ) dτ
∯ₛu⋅n dσ = ∫∫∫ᵥ∇⋅u dV
Trying to understand how that "energy" formula at the end is related to the more conventional energy formulas taught in mechanics classes is giving me a mild headache.
This sort of thing always gave me a headache though, and rotating space-time vectors around is so much simpler anyways.
no consideration for relativity theory?
see Hestenes' book "Spacetime Algebra"
02:30 Over m1.
no
What the fuck is watch product... you mean cross product?
wedge product. Cross product is only in 3D, wedge product can be in any number of dimensions.
@@Jason-mx5de lost to accent😁, thanks.
Haha, now you know 2 years later...
Sorry, but I believe this is not a great example to prove how powerful is geometric algebra 🫥