The clever way curvature is described in math
HTML-код
- Опубликовано: 8 фев 2025
- Second channel video: • What is "mean" about t...
How do mathematicians describe curvature of surfaces? There are two measures: Gaussian and mean curvatures, and both are useful in differential geometry, the study of surfaces and higher-dimensional manifolds (or lower-dimensional curves).
I know I have talked about Gaussian curvature before in this video: • Theorema Egregium: why... , but I want to reintroduce it slightly differently with a fuller explanation of the shape operator. This will allow mean curvature in the picture, and is something that I want to focus on for the two future videos on minimal surfaces.
I deliberately didn't say principal curvatures, which are the eigenvalues of the shape operator. The eigenvalues are guaranteed to be real, and the eigenvectors must also be orthogonal, because the shape operator is real and symmetric. However, getting to the point where we can prove the shape operator is real and symmetric is a bit tricky (can be proved rather easily with computations, but I'm not sure how to do it "intuitively"); and getting from real symmetric matrices to real eigenvalues and orthogonal eigenvectors is another thing that I still don't know how to think about intuitively.
This channel is meant to showcase interesting but underrated maths (and physics) topics and approaches, either with completely novel topics, or a well-known topic with a novel approach. If the novel approach resonates better with you, great! But the videos have never meant to be pedagogical - in fact, please please PLEASE do NOT use RUclips videos to learn a subject.
Files for download:
Go to www.mathemania... and enter the following password: shapeoperator
More on my criteria on choosing videos in #SoMEpi: www.mathemania...
Sources:
Paternain’s differential geometry notes www.dpmms.cam.... (see pp. 28 - 33)
Visual Differential Geometry and Forms by Tristan Needham
For this whole series, I have not consulted this book, but it should be a nice resource anyway for the geometric intuitions.
Soap film images:
commons.wikime...
commons.wikime...
Other than commenting on the video, you are very welcome to fill in a Google form linked below, which helps me make better videos by catering for your math levels:
forms.gle/QJ29...
If you want to know more interesting Mathematics, stay tuned for the next video!
SUBSCRIBE and see you in the next video!
If you are wondering how I made all these videos, even though it is stylistically similar to 3Blue1Brown, I don't use his animation engine Manim, but I use PowerPoint, GeoGebra, and (sometimes) Mathematica to produce the videos.
Social media:
Facebook: / mathemaniacyt
Instagram: / _mathemaniac_
Twitter: / mathemaniacyt
Patreon: / mathemaniac (support if you want to and can afford to!)
Merch: mathemaniac.my...
Ko-fi: ko-fi.com/math... [for one-time support]
For my contact email, check my About page on a PC.
See you next time!




![Felix "Unfair" | [Stray Kids : SKZ-PLAYER]](http://i.ytimg.com/vi/Oswujxm2Ag0/mqdefault.jpg)



First video of a trilogy about minimal surfaces - surfaces that minimise surface area given boundary conditions. Please LIKE, SUBSCRIBE, COMMENT as usual. The next video is how soap films take the shape they do (rather than why).
There are different conventions for the Gauss map: do you take the outward normal or inward normal? And what does outward or inward mean if the surface is not compact? There are also different conventions for the shape operator / second fundamental form, where you might see something like S(phi_u) = -n_u instead.
Regardless, all those conventions differ by negative signs, so it doesn't matter too much. (Except for the people who define mean curvatures in such a way that the mean curvature of a sphere is negative. Or people who define shape opeartor such that on the unit sphere it is not the identity map. What are you thinking?)
I remember my professor specifying that there are two different choices for the normal vector and you could choose whatever. (As long as it remains consistent of course)
5:07 for those who like me didn't understand the reason why the normal vector can only be assosiated with a point of the circle and not the whole sphere, just imagine moving it across the cylinder along v. As it stays perpedicular to the surface, it can only be directed toward a point on the circle
Thanks
Thank you so much!!!
Thank you for your contributions to this great channel.
Astonishingly clear and well written, with great animations, keep up this amazing work man!
Love this. I just finished studying these things this semester and you nailed it! I'm surprised you managed to not mention eigenvalues, but I think it's good, they weren't really necessary to the video.
The omission of eigenvalues is a deliberate choice. To justify eigenvalues being real takes a bit more time (and it requires something about real symmetric matrices), and I am not entirely sure why that theorem is intuitively true.
Great video and easy to follow explanations. Quick Tangent 😉: I went through all of this at university in our second year, and we only ever got two visual demonstrations/examples about this, and I was surprised it didn't come up here. It was about how Gaussian curvature is a measure of internal geometry and therefore independent of external transformations. Meaning if you roll a piece of paper into a cylinder, they will both have the same Gaussian curvature (namely zero). And for the same reason, a slice of pizza that is curved by gripping the crust and bending it will remain straight towards the tip and not bend downwards, because that shape would have positive Gaussian curvature, but pizza has a Gaussian curvature of zero, so that can't happen. In other words, you can't bend a flat surface in two directions at the same time.
Well I have made this exact video before! However that video signficantly underperformed, and I have already mentioned it in this video in hopes of bringing it to attention again (though it doesn't seem to help that this video is also significantly underperforming).
@@mathemaniac oh dang, sorry to hear that. Best of luck
Can't find that video. Do add a link, sounds exciting!
Btw this is a very important notion in physics! for example, even though the minkowsky metric is not trivial and on first glance things might look curvilinear, the space has 0 Gaussian curvature. Turns out - coordinates with 0 Gaussian curvature are exactly those frame where special relativity is sufficient to describe everything (if you are careful) and coordinates with non-zero curvature are exactly those where you get """gravity""". Both these notions must obviously be intrinsic properties of the space, rather than being representation dependent
Which makes perfect sense because only gravity contains acceleration. That being said, special relativity is also incomplete because accrleration is the only way to *change* speed. So reality has to be described by general relativity to be complete. This also cements "time" as illusory imo, the time variable judt represents relative differences in the speed of simultanious motion due to differences in the relative accelerations in other directions to that motion slowing down those relative motions with respect to each other. @@chalkchalkson5639
Thanks!
Please do more on differential geometry. Great video!
Mine are not as cool, but I have a full course. Come take a look ;)
Thanks!
In case you are somehow looking for subjects to cover in this series, I think it would be really cool to discuss how this framework generalises to Riemann manifolds and metric tensors. Not only because it's really neat to relate curvature and different notions of distance (like "how different are our longitudes and latitudes" vs "how many meters are we apart"), but also because it's always fun when geoemtry and fancy physics intersect :)
Fantastic video!
8:56 Gaussian Curvature in a sense is the measurement of how the surface can reshape to a flat plane without distortion. A paper can easily curve into a cylinder by just roll it up. So the curvature of a cylinder is 0.
TO EVERYBODY WHO READS THIS. Please upvote this video, and maybe let it play in the background multiple times, it's legitimately some of the best content on youtube, and it's not getting the views it deserves.
Since I've begun to work on videos of a similar genre and style, I know how much time and effort goes into not just creating, but VERIFYING everything, along with making sure its intelligible. It's wayyyy too easy to use math jargon and confuse the heck out of everyone watching. That he manages to break things down so well along with having stellar production value is not something the internet should take for granted.
Tl;dr I'm glazing mathemaniac but it's well deserved
Not sure about the playing in the background part, but thanks for your recognition of efforts.
@@mathemaniac Well... I understand that it's not exactly the best possible solution. But unfortunately this video isn't performing the greatest, and if someone, after they watch the video, lets it play in the background, then the watch time goes way up. Of course, this is your channel, but I am genuinely dismayed by seeing this incredible video not get the recognition it deserves
Thank you for this wonderful explanation.
Surprised how few comments this video has, so I'm leaving my own. Great content!
The legend is back
Really nice. I learned a lot 🤓👍
Great content.
يجب السرد التاريخي
ويجب تعريف الحاجه لهذه الرياضيات
الجميله
والأسباب الحقيقيه لوجودها
Great video! Since I majored in physics and studied GR, I'm wondering if you're gonna cover Riemann tensor, Ricci tensor, and Ricci scalar. Would be great to see how they are connected to these two types of curvature (or how perhaps they are the same as these two) 😃
Very unlikely that I will cover those because there are already many videos out there talking about this. What you have said is basically intrinsic curvature, while in this video, they are extrinsic curvatures.
However in 3D, the Theorema Egregium says that the Gaussian curvature is actually intrinsic.
Great video
I just learned all about this yesterday, what a crazy coincidence. Too bad I didn’t see this vid until now
Changing topic from Lie algebra...great... whatever topic you take we are with you!!! Thanks man...
Great Video, Never expected Curvature being measured via linear algebra, but makes sense in retrospect
Q: btw whats the background music? (ex: 1:50), it feels familiar…
I think the background music is automatically tagged by RUclips - just pull down the description to see. (These are copyright-free music provided by RUclips itself)
@@mathemaniac Thanks! Never knew that the auto tag feature existed (I should’ve scrolled a little further when checking the description)
Just curious based on your chosen topic: are you a fan of the works of Pavel Grinfeld (aka the mathisbeautiful channel guy)? Reading his texts really helped me wrap my mind around tensors, curvature, and minimal surfaces, not unlike your videos. And thanks for the channel, great stuff as always!
I have never heard of that person actually. Although for this video (or this coming series of videos) I haven't used it, the book Visual Differential Geometry and Forms by Tristan Needham is a gem.
"It's bendy..."
"It has the same shape as my girlfriend... (hubba hubba)"
I'm sure there are others that are nearly as descriptive. 😅😅😅
Who is, no doubt, Canadian, so no one else knows her.
Nice Video! Can you clarify how/if this applies to higher dimensional manifolds?
Usually it wouldn't be defined this way for higher-dimensional manifolds. You can search for second fundamental form (or extrinsic curvature) for how it applies to higher-dimensional manifolds.
Something about all this treatment is screaming "use geometric algebra" to me.
Well, the objects which measure the rate of change and live in the tangent plane are differential k-forms. The shape operator is in fact a geometric product, with the trace and and determinant being the two components of the geometric product, the inner and exterior products.
I was also thinking about GA during the video. Topology will remain stuck at surfaces unless they start using k-vectors.
new video!!
well made
i've been trying to work out something about the curvature of hyperboloids
clearly, a hyperboloid embedded in ordinary 3D space has a varying positive gaussian curvature
but, a hyperboloid generated by rotations in a minkowski space is a surface of uniform _negative_ curvature
this makes some sense given that it's effectively an anti-sphere, but how one would _calculate_ that curvature as negative has never been clear to me
but i'd previously been given oversimplified accounts of how gaussian curvature is calculated, so now i'm guessing that in this matrix-formulation the metric tensor has to be inserted somewhere somewhen (i've never liked the matrix formulations for minkowski spaces, because that "somewhere" and "somewhen" is deeply unintuitive to me)
Doesn't this definition of curvature with normal vectors require the existence of some ambient space?
yeah this is the extrinsic view of curvature (in the style of Oneill's Elemententary Differential Geometry)
Extrinsic and Intrinsic differential geometry are equivalent due to Nash Embedding Theorem
How do we describe all spirals and vortices?
Can someone explain to me (physics student) why they made us learn differential forms and pullbacks? And why you would ever need complex differential forms dz=dx+idy and dz*=dx-idy. I know how to compute stuff but I have zero idea how this relates to curvature
Im here trying to find out why a donut has zero curvature 😅
my maths brain hears: _B ϕ⃗ᵤ_
my linguistics brain hears: _bi faiyu_
Can somebody explain why w lies on tangent plane?
does the choice of the normal matter? it seems to me it could change the sign of curvatures
That's addressed in the pinned comments. It could change the sign of curvatures, but as long as you are consistent in your choice of normal, it doesn't matter.
is it Reimann Geometry that define Curvature
Riemannian
A fold is infinitely curvy?
Assuming the fold is a "limit" in the sense that the "turning radius" is getting smaller and smaller, then the Gaussian curvature is still 0, but the mean curvature diverges.
even just an edge between two faces has that property of det=0, tr/2=div
In the sphere map, the normal vector isn't on the surface of the sphere but at the origin...the sphere is the locus of the tip of all possible unit normals.
❤❤❤
Great video!
In cartography, there are a bunch of curvatures, but the two most popular are based on the radius of curvature of contour lines and the rate of change of slope along the steepest descent. They are available for the surface of the 🌏 at NASADEM….but they’re relative to the geoid, not the ellipsoid, and definitely not the tangent plane…so basically it’s a flat earth model because, ironically, that’s what geologists and hydrologists want.
Q: topologically similar shapes(for example, torus and tea cup) have the same overall curvature? Is this question even have meaning?(not matematician)
Well - I do plan on making a video on "total curvature" at some point, but not this time. (Probably the end of the year???) If you are a bit impatient, search for Gauss-Bonnet theorem.
Isnt there a torus that isnt curved? (the "pacman torus" or something)
Yes, but this video is only for surfaces in 3D. I think the flat torus cannot be embedded in 3D, and can only be embedded in 4D.
@@mathemaniacNo smooth embeddings exist, but C^1-isometric embedding of a flat torus in R^3 does!
g
Gaussian curvature discussed in other vid: ruclips.net/video/7Ju9f9odKX4/видео.html
I have already linked it in the description and the cards that are at the bottom of the description.
How ironic that you need to use straight lines to measure curvature. That just seems wrong. But it's apparant to me that gaussian curvature was the basis for gravitational probe b's measure of geodetics and frame dragging in earth's orbit.
One thing to keep in mind is thst straight lines are necessary for the existence of irrational lengths and numbers. The proof of the existence of irrationals *requires* straight lines, therefore if space is curved then it *must* also be discrete. And if it is curved and discrete, *then* the use of straight lines (via differentials) to *measure* curvature is unjustified and *wrong.* There must be a way of expressing curvature without using straight lines of any kind.
You can't describe curvature on point, only on a surface.
But surfaces are made of points.
Curvature can't exist, proved.
Rien compris
What is the curvature of an actual real tree? A shape that's like genus 10,000+ with insane topological complexity. Does the term "curvature" even apply to a shape of this complexity? Is there a tricky mathematical way to estimate the curvature despite it's complexity? And thirdly, what the heck is Poincare's conjecture? Oh yeah, and does the measure of curvature have anything to do with the measure of angles in 3 dimensions?
curvature in the sense it is used here is defined independently for each specific point on the surface, because different parts of an object can be curved differently. for example, the trunk of a tree, a branch thereof, and stems of its leaves all might be approximated as cylinders, at different rotations and scales, or perhaps as cones, which would just shift the circle the local normals describe a bit away from being in a plane with the origin in the direction the cone narrows to.
I should note that the definition was given in a very concise, but perhaos unintuitive way. Curvature, as used here, is a function, which belongs to an object, takes a point on the surface of that object, then looks at the transformation matrix describing what happens to the normal vector (aka "away" direction) when the point gets jiggled around slightly, and then returns one of two base-independent properties of that matrix. This means that curvature can be, and usually is, different depending on which point you select. Two points could have the same curvature, but in that case these points' immediate surroundings would usually look very similar.
Lindenmayer and Prusiencowics showed the geometry of plants and trees (really, nearly all biological growth) has fractal dimension.
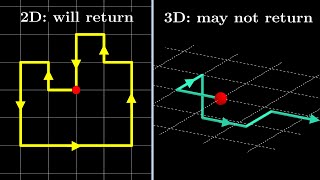
0:00 zero seconds in, wrong. n-punctured sphere, torus and Klein bottle all have constant Gaussian curvature of 0. So no, I can readily think of surfaces that are flat.
I should have said "embedded" surfaces. The surfaces you mentioned still has curvature (extrinsic) when embedded.
@@mathemaniacit depends entirely on the embedding. Take for example the embedding of the Klein bottle in E^4: (cos(v)cos(u), cos(v)sin(u), 2sin(v)cos(u/2), 2sin(v)sin(u/2)). This is an isometric embedding, hence the induced metric is the Euclidean metric.
Which has curvature, just extrinsic in 4D. The cylinder in 3D also has curvature because it has extrinsic curvature, even though of course its intrinsic curvature is 0.
@@mathemaniac no, the extrinsic curvature of the above embedding is 0. (Historically, mathematicians were unsure if one could even do this for the Klein bottle) Your initial point was the viewer couldn’t think of other flat surfaces. You then changed the point to finding an embedding where the extrinsic curvature is zero. You’re now wrong on two counts.
You can embed the an annulus in E^3 so that the extrinsic curvature is zero as well. I’ll leave that as an exercise as it is significantly simpler than the Klein bottle.
I can be wrong in this, but I'm not sure why the extrinsic curvature of the embedding is 0 in your parametrisation (or is that a typo?). I don't see how the normal vector can remain unchanged on the surface. Is there any reference for this? Equivalently, can you provide the normal vector that doesn't change across the surface?
The annulus has extrinsic curvature 0 because it is a part of a plane. Because its closure has a boundary, it isn't exactly comparable to the Klein bottle.
As far as I understand, if you want to have both intrinsic and extrinsic curvature 0 across all the surface, it has to be a part of a plane. The reason why I changed the point was my admission of omission of the condition that I wanted to specify in the first place, which should be clear from the context given in the entire rest of the video.
Sorry you lost me
And in 4 dimensions?
Thanks!