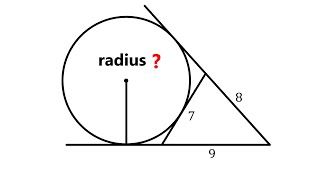
Can you find the missing side lengths of the triangle? | (Justify) |
HTML-код
- Опубликовано: 9 фев 2025
- Learn how to find the missing side lengths of the right triangle. Important Geometry and Algebra skills are also explained: similar triangles; Pythagorean Theorem; Euclid's Theorem. Step-by-step tutorial by PreMath.com
Today I will teach you tips and tricks to solve the given olympiad math question in a simple and easy way. Learn how to prepare for Math Olympiad fast!
Step-by-step tutorial by PreMath.com
• Can you find the missi...
Need help with solving this Math Olympiad Question? You're in the right place!
I have over 20 years of experience teaching Mathematics at American schools, colleges, and universities. Learn more about me at
/ premath
Can you find the missing side lengths of the triangle? | (Justify) |#math #maths | #geometry
Olympiad Mathematical Question! | Learn Tips how to solve Olympiad Question without hassle and anxiety!
#FindSideLengths #PythagoreanTheorem #Euclid'sTheorem #TriangleArea #GeometryMath
#MathOlympiad #IntersectingChordsTheorem #RightTriangle #RightTriangles
#PreMath #PreMath.com #MathOlympics #HowToThinkOutsideTheBox #ThinkOutsideTheBox #HowToThinkOutsideTheBox? #FillInTheBoxes #GeometryMath #Geometry #RightTriangles
#OlympiadMathematicalQuestion #HowToSolveOlympiadQuestion #MathOlympiadQuestion #MathOlympiadQuestions #OlympiadQuestion #Olympiad #AlgebraReview #Algebra #Mathematics #Math #Maths #MathOlympiad #HarvardAdmissionQuestion
#MathOlympiadPreparation #LearntipstosolveOlympiadMathQuestionfast #OlympiadMathematicsCompetition #MathOlympics #CollegeEntranceExam
#blackpenredpen #MathOlympiadTraining #Olympiad Question #GeometrySkills #GeometryFormulas #Angles #Height #ComplementaryAngles
#MathematicalOlympiad #OlympiadMathematics #CompetitiveExams #CompetitiveExam
How to solve Olympiad Mathematical Question
How to prepare for Math Olympiad
How to Solve Olympiad Question
How to Solve international math olympiad questions
international math olympiad questions and solutions
international math olympiad questions and answers
olympiad mathematics competition
blackpenredpen
math olympics
olympiad exam
olympiad exam sample papers
math olympiad sample questions
math olympiada
British Math Olympiad
olympics math
olympics mathematics
olympics math activities
olympics math competition
Math Olympiad Training
How to win the International Math Olympiad | Po-Shen Loh and Lex Fridman
Po-Shen Loh and Lex Fridman
Number Theory
There is a ridiculously easy way to solve this Olympiad qualifier problem
This U.S. Olympiad Coach Has a Unique Approach to Math
The Map of Mathematics
mathcounts
math at work
Pre Math
Olympiad Mathematics
Two Methods to Solve System of Exponential of Equations
Olympiad Question
Find Area of the Shaded Triangle in a Rectangle
Geometry
Geometry math
Geometry skills
Right triangles
imo
Competitive Exams
Competitive Exam
Calculate the length AB
Pythagorean Theorem
Right triangles
Intersecting Chords Theorem
coolmath
my maths
mathpapa
mymaths
cymath
sumdog
multiplication
ixl math
deltamath
reflex math
math genie
math way
math for fun
Subscribe Now as the ultimate shots of Math doses are on their way to fill your minds with the knowledge and wisdom once again.







❤❤❤❤❤
Thanks dear ❤️🙏
Nice! I used the Ratios behind the trigonometric identities (sin, cos & tan in terms of “opposite”, “adjacent” and “hypotenuse”) of the two similar triangles to reach the answers.
a=√[8²-5²]=√39
8h/2=5√39/2 8h=5√39 h=5√39/8
q=5*5/8=25/8
p=8-25/8=64/8-25/8=39/8
Can u write it properly???
Excellent!
Thanks for sharing ❤️
Thank you!
very good sharing bro thanks for sharing❤ stay connected keep it up🎉🎉🎉🎉🎉🎉🎉🎉
Thanks for visiting🌹
Thanks Prof. For your explaining this difficult situation
That’s very nice
Good luck with glades
❤❤❤
I took a order going through it, but got the same answers. Very satisfying.
You are a God in mathematics
I just made a table of the 3 similar triangles of "short side", "long side", and hypotenuse.
From 5 and 8 I immediately got sqrt(39). Then just ratioed the others for 5sqrt(39)/8, 39/8, and 25/8.
Final check was last, that the last 2 above totalled up to 8.
Didn't even have to do any 8-x as a side or anything. Took like 1min to just draw the 3 triangles and label the sides.
✨Magic!✨
can you explain haw are you writing alpha and beeta with no information, so please explain this
I accidentally stumbled onto a quicker way to find the length of q. Notice that triangle ABC is similar to ACD. That means AB/CA = CA/q. AB = 8 and CA = 5. So 8/5 = 5/q. Cross multiplying and simplifying, q = 25/8. As you did, Pythagorean formula finds a = sqrt(AB^2 - CA^2). Or a = sqrt(39). As you did, c = 8 - q or c = 64/8 - 25/8 = 39/8. h can be found by again comparing similar triangles. ABC is similar to CBD so AB/CA = CB/CD. That means 8/5 = a/h. Cross multiplying and solving for h: h = 5a/8. a = sqrt 39, so h = 5*sqrt(39)/8.
Thanks for sharing
I did the same.
Sir, by using Pythagoras theorem we can get BC directly.
It is sq.root of 64-25=39
That is BC is root 39.
We can easily find other sides using similarity of triangles.
Thanks for the feedback ❤️
In Right triangle ABC
b^2=q(c)
5^2=q(8)
So q=25/8
a^2=P(c)=(8-25/8)(8)
So a=√39
h^2=P(q)=(8-25/8)(25/8)=975/64
h=√975/64=5√39/8
So P=8-25/8=39/8.❤❤❤ Thanks Sir
Excellent!
You are very welcome!
Thanks for sharing ❤️
Let's find the missing side lengths:
.
..
...
....
.....
Let's have a look at the interior angles of all three right triangles ABC, ACD and BCD:
ABC: ∠ACB=90° ∠ABC=α ∠BAC=β
ACD: ∠ADC=90° ∠ACD=α ∠CAD=β
BCD: ∠BDC=90° ∠CBD=α ∠BCD=β
Therefore all these triangles are similar and we can conclude:
a:b:c = h:q:b = p:h:a
Additionally we can apply the Pythagorean theorem:
a² + b² = c²
a² + 5² = 8²
a² + 25 = 64
a² = 39
⇒ a = √39
b/c = h/a
⇒ h = a*b/c = 5√39/8
a/c = p/a
⇒ p = a²/c = 39/8
b/c = q/b
⇒ q = b²/c = 25/8
Best regards from Germany
Excellent!
Thanks for sharing ❤️
I got this one!
a=√64-25=√39. S= a*b/2≈c*h/2. h=a*b/c=5*√39/8. Далее по теореме Пифагора.
Excellent!
Thanks for sharing ❤️
I find these problems easier when using trigonometric identities. I also don't like leaving the answers in fraction form or as a multiple of a square root. I prefer the answers in a decimal form. These answers make more sense to me as an engineering technician, who had to find the sides of triangles in an effort to determine dimensions. In this case, the 5÷8 = arcsine beta, which is 38.68°. Now that I know the angle, I can use the trigonometric functions of the angle to determine the other sides of both smaller triangles. The side "a" then would 6.2449 which in the case of needing an answer in inches it would be rounded to 6 1/4 inches. If I was working 5 and 8 feet the answer would be 6 ft 2 15/16 in or 6 ft 3 in. Depending on the accuracy of the dimension required.
Very useful & informative video👍🏼thanks a lot🙋🏻♂️
Alternative way to get pq = SQR(h): Since ABC is a right triangle, use Thales theorem to see that BA is the diameter of a circle and C is a point on the circle. So intersecting chords get you p*q = h*h
That is a proof of Euclid theorim
Excellent!
Thanks for sharing ❤️
We are given that AC = b = 5, AB = c = 8, △ACB is right, and an altitude CD is shown, represented by h. Therefore, we can use the Geometric Mean Theorems to find a, h, p, & q (the altitude separates △ACB into two other right triangles, △ADC & △BDC, that are thus both similar to it by the Right Triangle Similarity Theorem).
First, use the Geometric Mean (Leg) Theorem.
(AC)² = AB * AD
5² = 8q
8q = 25
q = 25/8
= 3.125
So, BD = p = 8 - 3.125 = 4.875, or 39/8.
(BC)² = AB * BD
a² = 8 * 4.875
a² = 39
a = √39
≈ 6.24
Then, use the Geometric Mean (Altitude) Theorem.
(CD)² = AD * BD
h² = 3.125 * 4.875
h² = 975/64
h = √(975/64)
= (√975)/(√64)
= [(√25)(√39)]/[√(8²)]
= (5√39)/8
≈ 3.90
Alternatively, we could have used the Pythagorean Theorem after using the Geometric Mean (Leg) Theorem once, but this is the way I solved the problem.
So, the labeled side lengths are as follows:
a = √39 ≈ 6.24
b = 5
c = 8
h = (5√39)/8 ≈ 3.90
p = 39/8 = 4.875
q = 25/8 = 3.125
Very good representation and explanations 🎉🎉🎉🎉😊😊😊
Glad you liked it🌹
Thanks for the feedback ❤️
Here we have the Formula for this ;
(AC)² = (AD).(AB)
(BC)² = (BD).(BA)
(CD)² = (DB).(DA)
Thanks for sharing ❤️
The left side of the big triangle = ✓(8^2 - 5^2) = ✓39
black ? = 5 ÷ (8/✓39) = (5✓39)/8
red ? = 5 ÷ (8/5) = 25/8
blue ? = (✓39) ÷ (8/✓39) = 39/8
The RED line (q) is (bb/c) where b = 5 and c = 8 so ... 25/8 (3.125) in length.
From there, the black riser (h) is sqrt(b² + q²) = sqrt(5² + 25²/8²) = sqrt( 34.7656 ) = 5.896
Then (a) is pythagorean ... 8² - 5² = 64 - 25 = 39 ... sqrt(39) = 6.245
Lastly blue (p) is (aa/c) = 39/8 = 4.875
Just remember those 3 super identities about right triangles.
If sides are A, B and hypotenuse C then
Inside height is AB/C
A-side bit of C is AA/C. and
B-side bit of C is BB/C
FAST. Memorable. The Swiss-Army-Knife of your toolkit!
*In ABC: a^2 = BC^2 AB^2 - AC^2 = 64 - 25 = 39,
so a =sqrt(39).
*2.Area of ABC = a.b = 5.sqrt(39) = BC.DC = 8. h,
so h = (5/8).sqrt(39).
*BDC and CDA are similar (same angles),
so BD/BC = CD/CA, so p/sqrt(39) = ((5/8).sqrt(39))/5,
so p = 39/8.
*q = AD = AB -BD = 8 - (39/8) = 25/8.
It could be solved easily by similarity😂😂
Triangles ABC and ACD r equiangular.
8/5=5/DC
DC =25/8
AD=√(25 -625/64)
BD=8 -25/8
Then AB =√[(8-25/8)^2+25 - 625/64)]
Triangle ∆ACB:
AC² + CB² = BA²
5² + a² = 8²
a² = 64 - 25 = 39
a = √39
Excellent!
Thanks for sharing ❤️
My take: (1) Calculate on ABC using Pythagore: a=√39. (2) Calculate on ABC using both formulae for the surface: h=5√39/8. (3) Calculate p and q. More direct, easier to follow IMHO.
Just show the previous comment... Another way would be to use upfront the three similar triangles, not just two. Then explain which ratios are interesting, depending on the available data. Perhaps remind people that there are three ratios each time - a/b, a/c and b/c - and help them those that will lead more directly to the result. You could try to put them all on display, using different colors for numbers and variables, then highlithing the "good ones".
What is wrong with:
ACD is a right triangle. Set h=4, q=3 then b=5 due to Pythagorean theorem. Then p=8-3=5. Then due to Pythagorean theorem, a**2=(5**2) + (4**2), so a=sqrt(25+16)=sqrt(41)
My way of solution ▶
5²= q*c
c= 8
⇒
25= q*8
q= 25/8 length units
p= 8- 25/8
p= 39/8 length units
h²= p*q
h²= (39/8)*(25/8)
h= √975/64
h = √39*25/8
h = 5√39/8
a²+b²= c²
a²+5²= 8²
a= √39
b = 5, c = 8
p+q = c
===========
a² = c² - b²
a = √(c²-b²)
a = √(8²-5²)
a = √39
===========
a²-p² = h²
b²-q² = h²
a²-p² = b²-q²
a²-b² = p²-q²
39-25 = (p+q)(p-q)
14 = 8(p-q)
14 = 8p-8q
8p-8q = 14
8p+8q = 64 ---> (p+q = 8)8
------------ +
16p = 78
p = 39/8
========
8 = p + q
8 = 39/8 + q
64 = 39 + 8q
25 = 8q
25/8 = q
=========
h = √(a²-p²) or √(b²-q²)
h = √(a²-p²)
h = √(39-39²/8²)
h = √(39*8²/8²-39²/8²)
h = ⅛√(39*8²-39²)
h = ⅛√975
h = ⅛5√39
h = ⅝√39
h = √(b²-q²)
h = √(5²-25²/8²)
h = √(5²*8²/8²-25²/8²)
h = ⅛√(25*64-625)
h = ⅛√975
h = ⅝√39
p = 39/8, q = 25/8, h = ⅝√39 9:13
Solution:
Euclid's Pythagorean theorem: q*c = b² ⟹ q = b²/c = 5²/8 = 25/8
p = c-q = 8-25/8 = 64/8-25/8 = 39/8
Euclid's altitude theorem: h = √(p*q) = √(39/8*25/8) = 5*√39/8
Pythagoras: a = √(c²-b²) = √(8²-5²) = √39
STE-BY-STEP RESOLUTION PROPOSAL :
01) BC = a = sqrt(39) lin un ~ 6,245 li un
02) AC = b lin un = 5 lin un
03) AB = c lin un = 8 lin un
04) BD = p lin un ~ 4,875 lin un
05) AD = q lin un ~ 3,123 lin un
06) CD = h lin un = ((5 * sqrt(39)) / 8) lin un ~ 3,9 lin un
07) a^2 + b^2 = c^2 ; a^2 + 25 = 64 ; a^2 = 64 - 25 ; a^2 = 39 ; a = sqrt(39)
08) Right Triangle Area (A) = (a * b) / 2 ; A = ((5 * sqrt(39)) / 2) sq un ; A ~ 15,6 sq un
09) 2 * A = (h * c) ; 2 * ((5 * sqrt(39)) / 2) = 8 * h ; h = (5 * sqrt(39)) / 8 ; h ~ 3,9 lin un
10) q / b = h / a ; q / 5 = 3,9 / 6,245 ; q = (5 * 3,9) / 6,245 ; q ~ 3,123 lin un
11) p^2 = a^2 - h^2 ; p^2 = 39 - 975/64 ; p^2 = (2.496 - 975) / 64 ; p^2 = 1.521 / 64 ; p^2 ~ 23,8 ; p = 4,875 lin un
Thus,
OUR BEST ANSWER :
a ~ 6,245 li un
p ~ 4,875 lin un
q ~ 3,123 lin un
h ~ 3,9 lin un
Greetings.