RADICAL Math Problem Stumps 95% of People!

RADICAL Math Problem Stumps 95% of People!
Welcome to infyGyan dear viewer!
In today's video, we explore a fascinating algebra problem. If you love solving radical expressions then this is the perfect challenge for you. Join me as we work through this intricate algebra problem step-by-step. Don't forget to like, comment, and subscribe for more math challenges and solutions!
📌 Topics Covered:
Algebraic simplification
Algebraic manipulations
Problem-solving techniques
Algebraic identities
Competitive Math
🔢 What You'll Learn:
Key strategies for simplifying complex radical expressions
Tips and tricks to approach difficult simplification problems
Step-by-step walkthrough of the solution
🧠 Challenge Yourself:
Pause the video, try to solve the problem on your own, and then watch as we break down the solution. Share your approach and answers in the comments below!
👍 Don't Forget to:
1. Like the video if you found it helpful.
2. Subscribe for more Math Olympiad problems.
3. Hit the bell icon to get notified of new uploads.
4. Join us and enhance your problem-solving skills. Can you master this simplification problem?
Additional Resources:
• Thailand Math Olympiad...
• Brazilian Math Olympia...
• An Engaging Algebra Si...
• A Nice Algebra Simplif...
• Chinese | Math Olympia...
🔔 Don't forget to subscribe and hit the bell icon to stay updated with our latest math challenges and tutorials. If you enjoy the video, please give it a thumbs up and share it with your friends!
💬 Comment below if you have any questions or if you were able to solve the problem. We love hearing from our viewers!
Thank you for watching and happy problem-solving!
#simplification #matholympiad #algebra #problemsolving #learnmaths #mathtutorial #mathematics #education #educational #radical
Don't forget to like, share, and subscribe for more Mathematical content!
Thank You for Watching videos!!

[@ashokdubey8415]

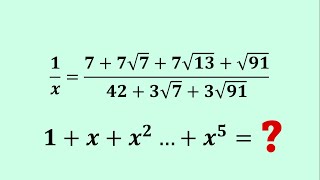
5:00 How did you conclude x>2 ?

[@RashmiRay-c1y]

E=[44√3 + 76]^1/5. So, E^5= 44√3 + 76 and let F^5= 44√3 - 76. Then (EF)^5 = 32 = 2^5. So, EF=2 and E^5-F^5=152. Let t = E-F. Then, t^5 + 10 t^3 +20 t = 152. So, t =2. With E-F=2 and EF=2 and with E positive, we get E = √3 + 1.

[@Quest3669]

?^5= 77+44√ 3 hence
?= √3+1 >0

[@潘博宇-k4l]

E=1+(3)^(1/2).

[@gregevgeni1864]

1+√3

[@walterwen2975]

RADICAL Math Problem: ⁵√[(√16 + √48)/(√49 - √48)] =?
(√16 + √48)/(√49 - √48) = 4(1 + √3)/(7 - 4√3) > 0
(√16 + √48)/(√49 - √48) = [4(1 + √3)(7 + 4√3)]/[(7 - 4√3)(7 + 4√3)]
= [(1 + √3)(4)(7 + 4√3)]/(49 - 48) = (1 + √3)(28 + 16√3)
(1 + √3)⁴ = [(1 + √3)²]² = (4 + 2√3)² = 4(2 + √3)² = 4(7 + 4√3) = 28 + 16√3
(√16 + √48)/(√49 - √48) = (1 + √3)(28 + 16√3) = (1 + √3)[(1 + √3)⁴] = (1 + √3)⁵
⁵√[(√16 + √48)/(√49 - √48)] = ⁵√[(1 + √3)⁵] = 1 + √3
Final answer:
(√16 + √48)/(√49 - √48) = 1 + √3

[@Fjfurufjdfjd]

χ=[76+44(3)^(1/2)]^(1/5)>0.καταληγω στο συστημα χ^5+ψ^5=152 χψ=-1 οπουψ=[76-44(3)^(1/2)]^(1/5)0
Για το α εχω α^5+10α^3+20α-152=0 (α-2)(α^4+2α^3+14α^2+28α+76)=0. Η δευτερη παρενθεση δεν εχει θετικη ριζα. Αρα α=2. χ+ψ=α>0 αρα χ=1+(3)^(1/2)

[@kaushalagrawal6258]

THIS LOOKS SO COOL

[@Fjfurufjdfjd]

Ευχαριστω.

[@ABHISHEKKUMAR-01024]

We have,
(√16 + √48) / (√49 - √48)
= (4 + 4√3) / (7 - 4√3)
= 4(1 + √3) / (7 - 4√3)
= 4(1 + √3)(7 + 4√3) / (7 - 4√3)(7 + 4√3)
= 4 { (7 + 4√3) + √3(7 + 4√3) } / { 7² - (4√3)² }
= 4 (7 + 4√3 + 7√3 + 12) / (49 - 48)
= 4 (19 + 11√3)
= 76 + 44√3
Let
⁵√{ (√16 + √48) / (√49 - √48) } = a
Then,
⁵√(76 + 44√3) = a
Also,
76 - 44√3
= 4 (19 - 11√3)
= 4 (19 - 11√3) (19 + 11√3) / (19 + 11√3)
= 4 { 19² - (11√3)² } / (19 + 11√3)
= 4 { 361 - (121 × 3) } / (19 + 11√3)
= 4 (361 - 363) / (19 + 11√3)
= - 8 / (19 + 11√3)
Therefore, 76 - 44√3 < 0
Now,
let ⁵√(44√3 - 76) = b, b > 0
Now, a⁵ = 76 + 44√3
and b⁵ = 44√3 - 76
=> a⁵ - b⁵ = 152
Also,
ab = { ⁵√(76 + 44√3) } { ⁵√(44√3 - 76) }
= [⁵√{4(19 + 11√3)}] [⁵√{4(11√3 - 19)}]
= ⁵√{ 16(19 + 11√3)(11√3 - 19) }
= ⁵√[ 16 {(11√3)² - 19²} ]
= ⁵√{16 (363 - 361) }
= ⁵√(16 × 2)
= ⁵√32
= 2
Now,
(a - b)⁵ = a⁵ - 5a⁴b + 10a³b² - 10a²b³ + 5ab⁴ - b⁵
= (a⁵ - b⁵) - (5a⁴b - 5ab⁴)
+ (10a³b² - 10a²b³)
= (a⁵ - b⁵) - 5ab(a³ - b³)
+ 10a²b²(a - b)
Now,
(a - b)³ = a³ - 3a²b + 3ab² - b³
= (a³ - b³) - (3a²b - 3ab²)
= (a³ - b³) - 3ab(a - b)
Therefore,
(a³ - b³) = (a - b)³ + 3ab(a - b)
Substituting,
(a - b)⁵ = (a⁵ - b⁵)
- 5ab {(a - b)³ + 3ab(a - b) }
+ 10a²b²(a - b)
= (a⁵ - b⁵) - 5ab(a - b)³
- 15a²b²(a - b) + 10a²b²(a - b)
= (a⁵ - b⁵) - 5ab(a - b)³ - 5a²b²(a - b)
= (a⁵ - b⁵) - 5ab(a - b)³ - 5(ab)²(a - b)
Substituting a⁵ - b⁵ = 152 and ab = 2,
(a - b)⁵ = 152 - 5(2)(a - b)³ - 5(2²)(a - b)
or, (a - b)⁵ = 152 - 10(a - b)³ - 5(4)(a - b)
or, (a - b)⁵ = 152 - 10(a - b)³ - 20(a - b)
or, (a - b)⁵ + 10(a - b)³ + 20(a - b) - 152 = 0
or, α⁵ + 10α³ + 20α - 152 = 0, where α = a - b
We have,
2⁵ + 10(2³) + 20(2) - 152
= 32 + 10(8) + 40 - 152
= 32 + 80 + 40 - 152
= 0
Therefore, α - 2 is one of the factors.
Then,
α⁵ + 10α³ + 20α - 152 = 0
or, α⁵ - 2α⁴ + 2α⁴ - 4α³ + 14α³ - 28α² + 28α²
- 56α + 76α - 152 = 0
or, (α⁵ - 2α⁴) + (2α⁴ - 4α³) + (14α³ - 28α²)
+ (28α² - 56α) + (76α - 152) = 0
or, α⁴(α - 2) + 2α³((α - 2) + 14α²(α - 2)
+ 28α(α - 2) + 76(α - 2) = 0
or, (α - 2) (α⁴ + 2α³ + 14α² + 28α + 76) = 0
or, α - 2 = 0, α⁴ + 2α³ + 14α² + 28α + 76 = 0
or, α = 2, α⁴ + 2α³ + 14α² + 28α + 76 = 0
Let us focus our attention on the root α = 2
Then a - b = 2
Also ab = 2
Now,
(a + b)² = (a - b)² + 4ab
= 2² + 4(2)
= 4 + 8
= 12
Therefore, a + b = 2√3
(We discard the - ve sign as a > 0 and b > 0)
Then,
2a = (a + b) + (a - b)
= 2√3 + 2
= 2(√3 + 1)
or, a = √3 + 1
or, ⁵√{ (√16 + √48) / (√49 - √48) }
= √3 + 1
The required answer.