A Very Nice Math Olympiad Problem | Solve for x | Algebra

In this video, I'll be showing you step by step on how to solve this Olympiad Maths Algebra problem using a simple trick.
Please feel free to share your ideas in the comment section.
And if you are new here and you enjoy my content, please hit the like button and subscribe to my channel. Don't forget to hit the bell icon as well so you don't miss on my upcoming videos.

[@MrPandaJJ]

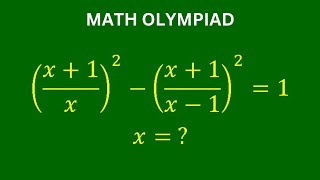
At the beginning of the 2nd page (~5:18), you know
x^4 - 4x^3 - 6x^2 - 4x + 1 = 0
Observe that flipping the sign of 6x^2 gives you (1-x)^4,
so we can in fact rewrite the equation as
(x^4 - 4x^3 + 6x^2 - 4x + 1) - 12x^2 = 0
i.e.
(1-x)^4 - 12x^2 = 0
This is the difference of two squares,
factorize it and you would get two quadratic equations, which give you the 4 solutions of x.
It would save you some times compare with the t substitution.

[@dan-florinchereches4892]

This is the solution I saw but later I also noticed this is a palindromic equation so dividing by x^2 can also work for it

[@SpencersAcademy]

Great job 👏

[@師太滅絕]

(continue) [(1-x)^2 - sqrt(12x)][(1-x)^2 + sqrt(12x)] = 0
case A (1-x)^2 - sqrt(12x) = 0
case B(1-x)^2 + sqrt(12x) = 0

[@MrPandaJJ]

@@師太滅絕
not sqrt(12x)
but sqrt(12)x
therefore much easier than you think

[@ernestdecsi5913]

A very nice solution indeed.

[@gintautasruksenas6129]

Ačiū!

[@SpencersAcademy]

My pleasure, sir 🙏
Thanks for the Super Thanks 😊
I'm indeed grateful 🙏

[@giuseppemalaguti435]

Risolvo la quartica..2+2x^4=1+6x+4x^2+6x^3+x^4..dopo i calcoli risulta (x^2-3x+1)^2-15x^2=0..poi è semplice .

[@MrPandaJJ]

At the end you say all 4 solutions are real not complex, however it is not true.
x_3 and x_4 are complex, as [3 - 2*sqrt(3)] is, in fact, negative.

[@JoseManuel-zn8lm]

Hola
Las soluciones son todas válidas al hacer la comprobación?
Gracias

[@SpencersAcademy]

Yes, they are.

[@jeanluchenry2152]

Pour x3,x4, c'est 2 nombres complexes car 3-2racine3 est négatif

[@souzasilva5471]

3-2V3 < 0 Logo sqrt(3-2sqrt(3) i

[@key_board_x]

(1 + x⁴)/(1 + x)⁴ = 1/2
2.(1 + x⁴) = (1 + x)⁴
2 + 2x⁴ = (1 + x)².(1 + x)²
2 + 2x⁴ = (1 + 2x + x²).(1 + 2x + x²)
2 + 2x⁴ = 1 + 2x + x² + 2x + 4x² + 2x³ + x² + 2x³ + x⁴
x⁴ - 4x³ - 6x² - 4x + 1 = 0 → the aim, if we are to continue effectively, is to eliminate terms to the 3rd power
x⁴ - 4x³ - 6x² - 4x + 1 = 0 → let: x = z - (b/4a) → where:
b is the coefficient for x³, in our case: - 4
a is the coefficient for x⁴, in our case: 1
x⁴ - 4x³ - 6x² - 4x + 1 = 0 → let: x = z - (- 4/4) → x = z + 1
(z + 1)⁴ - 4.(z + 1)³ - 6.(z + 1)² - 4.(z + 1) + 1 = 0
(z + 1)².(z + 1)² - 4.(z + 1)².(z + 1) - 6.(z² + 2z + 1) - 4z - 4 + 1 = 0
(z² + 2z + 1).(z² + 2z + 1) - 4.(z² + 2z + 1).(z + 1) - 6z² - 12z - 6 - 4z - 4 + 1 = 0
(z⁴ + 2z³ + z² + 2z³ + 4z² + 2z + z² + 2z + 1) - 4.(z³ + z² + 2z² + 2z + z + 1) - 6z² - 12z - 6 - 4z - 4 + 1 = 0
(z⁴ + 4z³ + 6z² + 4z + 1) - 4.(z³ + 3z² + 3z + 1) - 6z² - 16z - 9 = 0
z⁴ + 4z³ + 6z² + 4z + 1 - 4z³ - 12z² - 12z - 4 - 6z² - 16z - 9 = 0
z⁴ - 12z² - 24z - 12 = 0
z⁴ - (12z² + 24z + 12) = 0
z⁴ - 12.(z² + 2z + 1) = 0
z⁴ - 12.(z + 1)² = 0
z⁴ - [4.(z + 1)² * 3] = 0
z⁴ - [2².(z + 1)² * (√3)²] = 0
(z²)² - [2.(z + 1).√3]² = 0 → recall: a² - b² = (a + b).(a - b)
[z² + 2.(z + 1).√3].[z² - 2.(z + 1).√3] = 0
First case: [z² + 2.(z + 1).√3] = 0
z² + 2.(z + 1).√3 = 0
z² + 2z√3 + 2√3 = 0
Δ = (2√3)² - (4 * 2√3) = 12 - 8√3 ← it's negative → complex number
Δ = 12 - 8√3
Δ = - (8√3 - 12)
Δ = i².(8√3 - 12)
Δ = 4i².(2√3 - 3)
z = [- 2√3 ± 2i√(2√3 - 3)]/2
z = - √3 ± i√(2√3 - 3)
Second case: [z² - 2.(z + 1).√3] = 0
z² - 2.(z + 1).√3 = 0
z² - 2z√3 - 2√3 = 0
Δ = (- 2√3)² - (4 * - 2√3) = 12 + 8√3 = 4.(3 + 2√3)
z = [2√3 ± 2√(3 + 2√3)]/2
z = √3 ± √(3 + 2√3)
Recall: x = z + 1
When: z = - √3 ± i√(2√3 - 3)
→ x = 1 - √3 ± i√(2√3 - 3)
When: z = √3 ± √(3 + 2√3)
→ x = 1 + √3 ± √(3 + 2√3)

[@SpencersAcademy]

Incredible!!! 👏

[@RealQinnMalloryu4]

{1+1 ➖ }+{x^4+x^4 ➖ }/4x^4={2+x^8}/4x^4=2x^8/4x^4 2x^2^3/2^2x^2^2 1x^1^1^1/1^1x^1^2 x^1^2 (x ➖ 2x+1).

[@jimwinchester339]

Why not begin by cancelling out one of the powers of (x + 1) in the denominator with the numerator, then flipping over both sides of the equation, giving (x+1)^ 3 = 2? Surely that would be a lot simpler.

[@Lemda_gtr]

👍🏻🫡 waw great

[@milencenov6421]

4 real solutions ??? BS !!!
Note that √(3 - 2√3) is NOT real, because 3 - 2√3 is less than 0.
Also note that (x - 1)^4 expands very similarly to (x + 1)^4. All even powers are the same and the odd powers of x have minuses.
After you cross multiplied and rearranged, you could have noticed that:
(x - 1)^4 = 12 * x^2
Thus:
(x - 1)^2 = |x * 2√3|
(you may also write plus minus and normal brackets instead of the modulus)
Now you have the same 2 cases you arrived at.
x^2 - 2x + 1 = -x * 2√3
x^2 - 2(1 - √3)x + 1 = 0
Or
x^2 - 2x + 1 = x * 2√3
x^2 - 2(1 + √3)x + 1 = 0
Note that when B is equal to -2(1 - √3), the discriminant is negative, because B^2 < 4AC.