
- Видео 106
- Просмотров 7 127
Reza Razavian
США
Добавлен 11 окт 2013
Dynamics - kinetics of a system of particles
Dynamics - kinetics of a system of particles
Просмотров: 0
Видео
Dynamics - remarks about Newton's equation
Просмотров 29 часов назад
Dynamics - remarks about Newton's equation
Dynamics - kinetics in cylindrical frame
Просмотров 19 часов назад
Dynamics - kinetics in cylindrical frame
Dynamics - kinetics in tangential/normal frame
Просмотров 19 часов назад
Dynamics - kinetics in tangential/normal frame
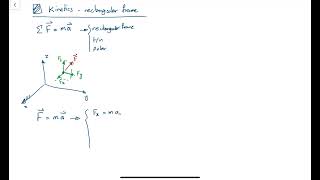
Dynamics - kinetics in rectangular frame
Просмотров 19 часов назад
Dynamics - kinetics in rectangular frame
Dynamics - polar frame - position and velocity
Просмотров 53День назад
Dynamics - polar frame - position and velocity
Dynamics - tangential/normal frame - position and velocity
Просмотров 6314 дней назад
Dynamics - tangential/normal frame - position and velocity
Dynamics - tangential/normal frame - acceleration
Просмотров 7414 дней назад
Dynamics - tangential/normal frame - acceleration
Dynamics - tangential/normal frame - remarks
Просмотров 5914 дней назад
Dynamics - tangential/normal frame - remarks
Dynamics - Curvilinear motion - acceleration
Просмотров 6921 день назад
Dynamics - Curvilinear motion - acceleration
Dynamics - Curvilinear motion - velocity
Просмотров 6621 день назад
Dynamics - Curvilinear motion - velocity
Dynamics - Curvilinear motion - position
Просмотров 6821 день назад
Dynamics - Curvilinear motion - position
Dynamics - Constant acceleration motion
Просмотров 5821 день назад
Dynamics - Constant acceleration motion
Dynamics - Integrals of kinematics variables
Просмотров 4321 день назад
Dynamics - Integrals of kinematics variables
Dynamics - Rectilinear motion of a particle - velocity
Просмотров 5521 день назад
Dynamics - Rectilinear motion of a particle - velocity
Dynamics - Rectilinear motion of a particle - remarks
Просмотров 6321 день назад
Dynamics - Rectilinear motion of a particle - remarks
Dynamics - Rectilinear motion of a particle - acceleration
Просмотров 6721 день назад
Dynamics - Rectilinear motion of a particle - acceleration







I loved your comment in 12:50 "I do not know where it is coming from, ask Euler"
Thank you so much sir, thanks to your clear explanation, I can now make sense of Euler rotations
P r o m o s m 😱
Is w in body fixed frame here? Or do we need to premultiply with R(world to body)?
These omega_x, omega_y, omega_z are in the body-fixed frame.
"Promo sm"
This video saves my life
😲 I made a mistake! Bandwidth is -3dB not -20dB!