
- Видео 36
- Просмотров 24 486
DrY♥Lab
Добавлен 25 янв 2023
楊老師失業了! 不能做實驗。︁「Dry lab」是「乾實驗室」而不用化學試劑。︁他研究生物,醫學和納米科技也教化學,數學和生物。︁可憐的楊老師希望用RUclips幫他找工作。︁
♥
A "dry lab" is a place for technical work that does not involve actual chemicals. Instead, we use theories and calculations. Dr Yang has a dry lab because he is unemployed from working as a biomedical and nanotechnology researcher. He also teaches chemistry, calculus, and biology. Lucky for you, Dr Yang is resorting to make RUclips videos in trying to find jobs.
♥
Original content © Jung-Lynn Jonathan Yang
DrY♥Lab is a trademark by Jung-Lynn Jonathan Yang
♥
A "dry lab" is a place for technical work that does not involve actual chemicals. Instead, we use theories and calculations. Dr Yang has a dry lab because he is unemployed from working as a biomedical and nanotechnology researcher. He also teaches chemistry, calculus, and biology. Lucky for you, Dr Yang is resorting to make RUclips videos in trying to find jobs.
♥
Original content © Jung-Lynn Jonathan Yang
DrY♥Lab is a trademark by Jung-Lynn Jonathan Yang
Introduction to matrices: 2 equations, 2 unknowns in augmented matrix
𝗟𝗘𝗔𝗥𝗡𝗜𝗡𝗚 𝗢𝗕𝗝𝗘𝗖𝗧𝗜𝗩𝗘
♥ Solve a system of equations by row reducing an augmented matrix.
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡
Solve the system of equations.
2𝑥 + 3𝑦 = −5
−𝑥 + 7𝑦 = 11
𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪
A matrix looks scary but can be thought of as another way to organize numbers. An example of using matrices is solving systems of equations. In high school, I learned to solve by substituting one equation into another (0:05) and by adding/subtracting equations (1:50). The goal is to eliminate the number of unknown variables. When there is one unknown in a single equation, that is when we can solve for the value of the unknown.
A more sophisticated way to solve the system of equations is to row reduce an augmented matrix (3:15). Get as man...
♥ Solve a system of equations by row reducing an augmented matrix.
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡
Solve the system of equations.
2𝑥 + 3𝑦 = −5
−𝑥 + 7𝑦 = 11
𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪
A matrix looks scary but can be thought of as another way to organize numbers. An example of using matrices is solving systems of equations. In high school, I learned to solve by substituting one equation into another (0:05) and by adding/subtracting equations (1:50). The goal is to eliminate the number of unknown variables. When there is one unknown in a single equation, that is when we can solve for the value of the unknown.
A more sophisticated way to solve the system of equations is to row reduce an augmented matrix (3:15). Get as man...
Просмотров: 83
Видео
Trigonometric integrals, ∫ sinᵐ 𝑥 cosⁿ 𝑥 d𝑥, odd powers
Просмотров 170Месяц назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Solve the integrals. 0:47 ∫ sin³ 𝑥 cos⁴ 𝑥 d𝑥 2:28 ∫ sin⁴ 𝑥 cos³ 𝑥 d𝑥 3:33 ∫ sin⁵ 𝑥 cos⁵ 𝑥 d𝑥 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 These integrals have sine and cosine multiplied together, and at least one of these trigonometric functions have a 𝗽𝗼𝘀𝗶𝘁𝗶𝘃𝗲, 𝗼𝗱𝗱 power. ① Find a trig function with the positive, odd power and save one factor of this trig function. ② Express the remaining factors of this trig function a...
Lewis structure example, Everyday Molecules Edition 1: H2O, O2, CO2, N2
Просмотров 642 месяца назад
𝗟𝗘𝗔𝗥𝗡𝗜𝗡𝗚 𝗢𝗕𝗝𝗘𝗖𝗧𝗜𝗩𝗘𝗦 ♥ Draw Lewis structures of molecules. ♥ Assign formal charges to atoms in molecules. 💡 𝗥𝗘𝗠𝗘𝗠𝗕𝗘𝗥 ♥ The number of valence electrons corresponds to the last digit in the group number on a periodic table. ♥ Each atom, especially C, N, O, and F, in a molecule has an 𝗼𝗰𝘁𝗲𝘁, a total of 8 electrons, counting all the electrons attached to the atom. Do not split bonds. Splitting bonds...
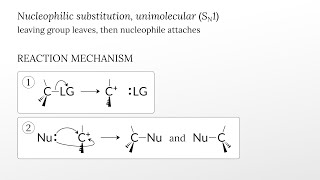
Unimolecular nucleophilic substitution (SN1), overview
Просмотров 274 месяца назад
TRANSCRIPT There are two elementary steps in the SN1 reaction mechanism. The first step is the departure of the leaving group (LG). The leaving group takes the two bonding electrons as a lone pair and detaches from the carbon atom. The loss of electron from carbon confers a positive charge in the carbocation intermediate. In the second step, a lone pair from a nucleophile (Nu) forms a bond to t...
Differentiate (sin θ)ᶜᵒˢ ᶿ and (𝑥 + sec 𝑥)⁴ᐟˣ
Просмотров 1776 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Differentiate 0:03 𝑟(θ) = (sin θ)ᶜᵒˢ ᶿ 2:40 𝑦(𝑥) = (𝑥 sec 𝑥)⁴ᐟˣ 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 When a variable appears in both the base as well as the exponent, use 𝗹𝗼𝗴𝗮𝗿𝗶𝘁𝗵𝗺𝗶𝗰 𝗱𝗶𝗳𝗳𝗲𝗿𝗲𝗻𝘁𝗶𝗮𝘁𝗶𝗼𝗻. Take the natural log of the entire equation to bring down the exponent. Differentiate by the Product Rule or Quotient Rule. A summary of the steps is as follows: ① Take the natural logarithm (ln) of both sides of the...
Differentiate (𝑥² + 1)(7𝑥 − 6)⁵(𝑥 − 3) / [ (cos(𝑥) + 2) eᵉᕽ ]
Просмотров 946 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Differentiate (𝑥² 1)(7𝑥 − 6)⁵(𝑥 − 3) / [ (cos(𝑥) 2) eᵉᕽ ] 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 Although we can differentiate a huge product or quotient by the Product Rule or Quotient Rule, doing so is tough because there are so many factors to keep organized. Instead, we use the technique of 𝗹𝗼𝗴𝗮𝗿𝗶𝘁𝗵𝗺𝗶𝗰 𝗱𝗶𝗳𝗳𝗲𝗿𝗲𝗻𝘁𝗶𝗮𝘁𝗶𝗼𝗻: 0:10 ① Take the natural logarithm (ln) of both sides of the equation. 0:13 ② Separate factors...
Chain Rule examples
Просмотров 1516 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Differentiate these functions. (0:01) 𝑦(𝑥) = eˣ² (0:23) 𝑔(𝜃) = sec(sin(tan √𝜃³)) (1:36) 𝑓(𝘵) = 5/(cos(eᵗ²⁻⁷ᵗ⁺¹))² It is not necessary to simplify the derivative. 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 A composite function is a function with one or more functions nested inside. The Chain Rule tells us to differentiate composite functions, starting from the outermost function and working inward. Keep any arguments of...
Differentiate these logarithmic functions
Просмотров 717 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Differentiate these functions. (0:03) 𝑟(𝜃) = log₁₀ 𝜃 (0:25) 𝑔(𝑥) = log₂ ( 𝑥 (𝑥 1) (𝑥 2)³ ) (2:22) 𝑦(𝑢) = log₍ᵤ₊₁₎ 𝑢 It is not necessary to simplify the derivative. 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 Memorize the derivative rules for a general logarithm (base-𝑎) and the natural logarithm (ln) in order to differentiate logarithmic functions. Also, memorize the 𝗽𝗿𝗼𝗽𝗲𝗿𝘁𝗶𝗲𝘀 𝗼𝗳 𝗹𝗼𝗴𝗮𝗿𝗶𝘁𝗵𝗺𝘀 and the 𝗰𝗵𝗮𝗻𝗴𝗲 𝗼𝗳 𝗯𝗮𝘀𝗲 formu...
Find 𝑐 › 0 for crit pt in 𝑟(𝑡) = (𝗅𝗇(𝑐𝑡² − 2𝑐𝑡 + 2𝑐))²
Просмотров 868 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Find the value of the constant 𝑐 › 0 such that there are critical points at 𝑡 = 0, 1, 2 in the function 𝑟(𝑡) = (𝗅𝗇(𝑐𝑡² − 2𝑐𝑡 2𝑐))². 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 At a 𝗰𝗿𝗶𝘁𝗶𝗰𝗮𝗹 𝗽𝗼𝗶𝗻𝘁, the first derivative is equal to zero. Differentiate 𝑟(𝑡) by Chain Rule; set 𝑟′(𝑡) equal to 0 at 𝑡 = 0, 1, 2; and solve for 𝑐. Often, the question tells/implies us to solve for 𝑥-values, here we have 𝑡-values, that makes the f...
Find 𝑎 for crit pt in 𝑔(𝑥) = 𝑥𝚎ᵃˣ at 𝑥 = 1/3
Просмотров 598 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Find the value of the real constant 𝑎 such that the function 𝑔(𝑥) = 𝑥𝚎ᵃˣ has a critical point at 𝑥 = 1/3. 𝗪𝗢𝗥𝗞𝗙𝗟𝗢𝗪 At a 𝗰𝗿𝗶𝘁𝗶𝗰𝗮𝗹 𝗽𝗼𝗶𝗻𝘁, the first derivative is equal to zero. Differentiate 𝑔(𝑥) by Product Rule; substitute 𝑥 = 1/3 into 𝑔′(𝑥); set 𝑔′(1/3) to zero; and solve for 𝑎. Often, the question tells/implies us to solve for 𝑥-values that makes the first derivative equal to zero in ...
Global/relative min/max of 𝑓(𝑥) = 𝑥¹ᐟ³ + 𝑥²/6 in −8 ≤ 𝑥 ≤ 1
Просмотров 708 месяцев назад
𝗤𝗨𝗘𝗦𝗧𝗜𝗢𝗡 Identify the absolute (global) extrema and relative (local) extrema of the function, 𝑓(𝑥) = 𝑥¹ᐟ³ 𝑥²/6 within the interval −8 ≤ 𝑥 ≤ 1. Are you wondering what is happening at 𝑓(0)? It is a continuous point on the graph that has a vertical tangent line. The vertical tangent line makes the derivative undefined, i.e. a singular point, but, in this case, is not a minimum or maximum. Therefor...
Singular Point (Work-in-Progress)
Просмотров 2111 месяцев назад
January 1, 2024 "Singular Point" pictorial summary by Jung-Lynn Jonathan Yang. Work-in-progress.
Second Derivative Test (Work-in-Progress)
Просмотров 7911 месяцев назад
January 1, 2024 "Second Derivative Test" pictorial summary by Jung-Lynn Jonathan Yang. Work-in-progress.
Second Derivative Test Fails (Work-in-Progress)
Просмотров 6511 месяцев назад
Second Derivative Test Fails (Work-in-Progress)
First Derivative Test (Work-in-Progress)
Просмотров 2111 месяцев назад
First Derivative Test (Work-in-Progress)
呷蝦咪 T&T Supermarket (大統華) Mooncake Review
Просмотров 284Год назад
呷蝦咪 T&T Supermarket (大統華) Mooncake Review
Factoring [Example] [Algebraic limits]
Просмотров 2,7 тыс.Год назад
Factoring [Example] [Algebraic limits]
Combining techniques [Example] [Algebraic limits]
Просмотров 733Год назад
Combining techniques [Example] [Algebraic limits]
Multiplying by the conjugate [Example] [Algebraic limits]
Просмотров 13 тыс.Год назад
Multiplying by the conjugate [Example] [Algebraic limits]
Combining fractions [Example] [Algebraic limits]
Просмотров 386Год назад
Combining fractions [Example] [Algebraic limits]


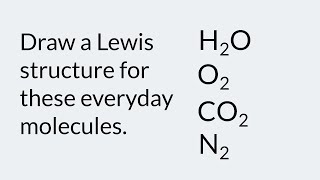

![Differentiate (𝑥² + 1)(7𝑥 − 6)⁵(𝑥 − 3) / [ (cos(𝑥) + 2) eᵉᕽ ]](http://i.ytimg.com/vi/kW6Oeia4DL0/mqdefault.jpg)



I love ❤️ it! Thank you! Now things are so much clearer!
Wow i love this video please i need more even on physics and chemistry
Clear presentation on how to execute the Chain Rule correctly on given compositie functions ... best regards, gui
If Y=1/2√x
Sorry, I did not understand your question! Could you tell me more?
Good evening ask questions
? Bernulli Lopital is faster!
In the first few lessons of Calculus I, we are told to solve limits algebraically and do not use l’Hôpital's Rule. Although, if the teacher does not specify which method to use, or not to use, then yes, use l’Hôpital's Rule because it is faster!
"Why don't use L'Hopital?", one may ask. Well, it depends on the purpose. Since you need to learn limits in order to learn derivatives in a standard calculus 1 course, you will face many 0/0 limits where you will be required to solve algebraically before being introduced to the concept of derivatives. Every year at my college I face myself trying to help new students to manipulate a limit where L'Hopital would solve in two lines, just because they are in the beginning of the course haha
This is exactly what I have to do for teaching calculus! It's neat that we use limits to evaluate derivatives and then use derivatives, in the form of l'Hôpital's Rule, to solve limits.
6^-1
That is the correct answer!
Do more of these examples with trig functions too.
meanwhile i'm just using l'hopital rule
Yes, use l’Hôpital's Rule if the question does not tell you not to use it! In the calculus courses I took and have to teach, we could only use algebraic techniques and were not allowed to use l’Hôpital's Rule in the unit about limits.
I think actually the conjugate is way faster because of the x - 7 cancellation but I like how l'hopital is more general so honestly me too
Neat! Multiplying by the conjugate may be faster because the root differentiates by the Chain Rule, which brings in more factors to deal with and makes l’Hôpital's Rule a bit complicated. Alternatively, we can try a mix of both methods! Start with multiplying by the conjugate, then as long as the indeterminate form is appropriate (±∞/±∞ or 0/0), use l’Hôpital's Rule. Whatever method you prefer, use the method that works fastest and most accurately for you and is also allowed by the exam instructions.
🎉hey 👋🏻☺️👋🏻😊😌🤗@
Good 👍
Good
Is this AP calculus level or easier?
Good question, I actually don't know! I think factoring to solve limits is typical of Advanced Placement (AP) calculus and definitely university/college calculus. According to page 40 of “AP Calculus Course and Exam Description” (apcentral.collegeboard.org/media/pdf/ap-calculus-ab-and-bc-course-and-exam-description.pdf), “[f]actoring and dividing common factors of rational functions” looks to me like this video is typical of what is on the AP curriculum.
❤
The best video
that is way to specific. no way anyone would prefer this over l'hopital which is both easier to use and more general.
There is a lot of annoying algebra! For some reason, I had to learn this as a student and is also in the curriculum I teach in multiple universities. L'Hôpital's Rule is easier and faster.
Why didn't you conjugate (x-7) with (x+7)?
Good question! When we multiply (x − 7) and (x + 7), we have the difference of squares x² − 49, which does not cancel much. Instead, if we target the awkward square root, then we can eliminate the square root as a difference of squares.
Wow I really liked that little flashcard for Conjugate
It is the literal definition of the derivative of f(x) = sqrt(x+2) at x = 7
Good call! It is! I think this is why calculus courses begin with limits because then we can extend limits to the limit definition of the derivative.
Thanks a lot professor I follow you from Algeria.
I am not officially a professor because I am unemployed. I do things that professors do, like teaching, supervising undergraduate/graduate research projects, and evaluating funding applications. Thank you for watching!
great video!
Couldnt u just do l'hopital?
Absolutely, l’Hôpital’s Rule is another way to solve this limit question! In fact, l’Hôpital’s Rule is applicable for limits of the form “0/0” (what we have here) and “±∞/±∞”. In the beginning lessons and midterm(s) in Calculus I, instructors tend to tell students to solve limits using algebraic methods rather than l’Hôpital’s Rule. However, if the question does not specify which method to use, l’Hôpital’s Rule can be an easier and faster method than algebra.
Did it orally by just rationalising
That is great to be able to solve this question mentally (by inspection)! Solving mentally is especially suitable on questions where it is not necessary to show calculation work, like multiple choice questions.
Thank you
But since the limit for 7 of numerator and denominator are both equal to zero, L”Hospital’s rule works very well.
You are right! L'Hôpital's Rule is perfect for indeterminate forms “0/0” (the situation here) and “±∞/±∞”. In the calculus courses I took and taught, we had to solve limits algebraically. On my midterm exam, the instruction specifically told us to not use L'Hôpital's Rule. It was not until later on in the course, about applications of derivatives, that we had the option of L'Hôpital's Rule.
Thank you. Sorry for the advance@@DrYheartLab
I am glad you brought up l’Hôpital’s Rule! If the question does not specify which technique to use, or not to use, l’Hôpital’s Rule is often a faster method than algebra.
... Good day, Observing the expression of the limit ( SQRT(X + 2) - 3 ) / ( X - 7 ), I see the occasion to rewrite the denominator ( X - 7 ) as follows ... X - 7 = ( X + 2 ) - 9 , and treat ( X + 2 ) - 9 as a " Difference of 2 Squares " ... ( X + 2 ) - 9 = [ SQRT(X + 2) - 3 ] * [ SQRT(X + 2) + 3 ] ... now recognizing a common factor between numerator and denominator expression of [ SQRT(X + 2) - 3 ] ... which simplifies the original limit as .... LIM(X->7)[ 1 / ( SQRT(X + 2) + 3 ) ] = 1 / ( SQRT(9) + 3 ) = 1 / ( 3 + 3 ) = 1/6 ... solving this limit exercise by applying " Factoring the Denominator " ... thanking you DrY(black heart)Lab for your instructive presentation .... best regards, Jan-W
Amazing, @Jan-W, I could not have thought of your solution! Absolutely, write the “x − 7” as “(x + 2) − 9” and then factor as a difference of squares to cancel with the numerator. I am glad you brought up this alternative solution! 💡
Thats splendid. I would not be able to come up with that in 1000 years!!
Not to worry! There may be multiple ways to solve limits. Just use what works well and accurately for you.
金風送爽 丹桂飄香 傳說吟唱 南北百味 揉方糰圓 歡喜香甜
愛城冬夏季氣溫零上零下30 多度, 挺有趣的, 真想試試潑水成冰的把戲
Needs museum gloves to open such a luxurious combo 😂😂😂😂😂 Thanks so much for such a detailed and informative review of mooncakes. Always so hard to know what to buy so you really help us save money and pick the variety that works for what we want to eat. And thanks for the warning about no meat!! What a tricky piece of labelling indeed!
Every year hundreds luckily bought and thousands fortunately ate but only very few could tell so well.
Outstanding pictures and interesting details about the art in these festival celebration. Wonderful job. 🎉🎉
Good job 👌👍
😅😅 very harsh subject to understand
It can be quite an abstract topic! The usual example is the sodium-potassium pump. I included some uncommonly used examples to show that there are other ways to use ATP and also sources of energy other than ATP, like the ATP-binding cassette transporter, light-gated ion channel, and electron transport chain. Let me know if there is another method of presenting the subject that is more understandable!
I loved this!! So witty AND informative! 🎉😂
Isn't that the definition of a Bronsted acid ?
Glad you asked! Arrhenius acids are a subset of Brønsted-Lowry acids, which are a subset of Lewis acids, the most general category of acids in some university programs. All the acids in this video are Arrhenius acids and thus are also Brønsted-Lowry acids. The Arrhenius definition of acid is quite narrow about 1) hydrogen ion (H⁺, proton) and 2) in water. The idea of a free H⁺ floating in solution is not the best description because a free H⁺ is too unstable. The Brønsted-Lowry definition is broader; acids are H⁺ donors in water and also in other environments, such as the gas phase. Also, the Arrhenius definition does not say where the H⁺ goes. Brønsted-Lowry-type of reactions necessarily involve an acid-base pair of reactants. The H⁺ does not float around like in the video for the Arrhenius definition. According to Brønsted-Lowry, the HCl in water has to donate H⁺ to something. If there is no other H⁺ acceptor other than water, then water is the reactant that accepts H⁺ from HCl. The free H⁺ is too unstable, but H₃O⁺, a water molecule that accepted H⁺, has been observed.
Thank you very much Dr. Y. I can see from your eyes and understand the theory in lab action.
Thank you very much Dr. Y. This very new lab action video helps me to see the true meaning of the importance of the theory.
Wonderful story about Edmonton
Now I can understand. Thank you very much for your help Dr Y Lab
A lot useful educational information and very interesting to watch over and over again