Видео

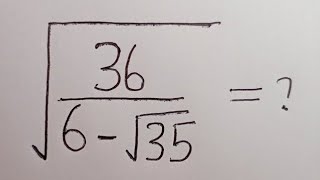
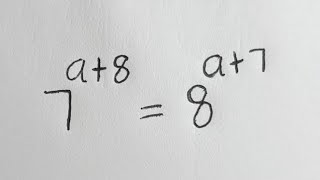
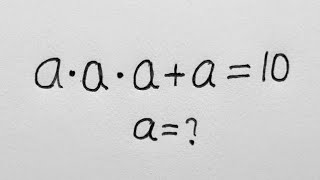
x^(1/2+1/4+1/8+1/16+1/32)=x^(31/32) =8 x=8^(32/31)

a=5/2+c & b=5/2-c; (5/2+c)(5/2-c)=8; c^2=25/4-32/4=-7/4; c=±i√7/2; a=(5±i√7)/2 & b=(5∓i√7)/2

√(x*√(x*√(x*(√x*√x))))=8 x*√(x*√(x*(√(x*√x)))=8^2 x^3*√(x*(√(x*√x))=8^4 x^7*√(x*√x)=8^8 x^15*√x=8^16 x^31=8^32 x=8^(32/31) x=8.555037588568538...

Это шутка?

Substitute t=10^x and recall that 100^x=(10^x)^^2 and 1000^x=(10^x)^3. Than you get t+t^2=t^3 t^3-t^2-t=0 t*(t^2-t-1)=0 t=0 or t^2-t--1=0 t=0 or t=(1+sqrt(5)/2 or t=(1+sqrt(5)/2 Reember, tht t=10^x>0, so t=0 and t=(1-sqrt(5) willll be rejected So we get 10^x=(1+sqrt(5)/2 x=llog((1+sqrt(5))/2)

a+b=100 ab=1000. 90+10=10] 9p.10=90] Imrightmaster?? a+b=c cb=d cb=1000 100×10=1000❤❤😂😊🎉

You have taken long time shortcut methods are there

Ответ - 5. Практически сразу.

x^3+/-x^2+/-x-64=0 , (x-4)(x^2+4x+16)=0 , x^2+4x+16=0 , x=(-4+/-V(16-64))/2 , x=(-4+/-i*V(48))/2 , x=(-4+/-i*4V(3))/2 , 1 -4 solu , x= 4 , -2+i*2V3 , -2-i*2V3 , 4 -16 16 -64

a=2

x=4 or x= -2±2i×sqrt3

2^x=a a³-a=120 5³-5=125-5=120 a=5 2^x=5 x=log5/log2= x≈0.699/0.301≈2.322 Deviation is about 0.0003 8^2.322-2^2.323≈120.018

8 + 2 = 10

Wrong solution. Should be square -48 not -58.

(a-b) ^2=(a+b) ^2 - 4ab =10000-4000 =6000 =100×60 Or (a-b) =10√60 Now a+b=100 a-b=10√60 Next 2a =100+10√60 Or a=50+5√60 and b=50-5√60

Gud sir thankx my dear

Wonderful and respected. 🙏💖

-5. 25-(-125)=150

An easy problem, but I wonder why you chose such large numbers that are prime for the solution set. It’s just makes the arithmetic a little harder, but I don’t see the point.

my answer is x=51/2 1/2 and y = 49/ 2 1/2; do not know how to type root of 2 square; any catch for this problem?

Best Trick? a=97/2+c, b=97/2-c, (97/2+c)(97/2-c)=997, c^2=97^2/4-997=5421/4, a=(97+√5421)/2, b=(97-√5421)/2

Мало знаков, добавить ещё 5😅😅😅

√(x√x........)=x^(31/32) ; so, x^(31/32)=8 ; i,e x=8^(32/31) ; i,e x=2^(3×32/31) ; i,e x= 2^(96/31)

I have to study my log rules.

well done! 😃

Is it really Math OLYMPIAD Problem?? REALLY??

Very nice solutions

writing correctly your signs, your letters and your numbers will ease the understanding of your demonstration thanks for this help anyway

You lost third answer x=-0.766665

I wish people would stop using Olympiad to attract views of very straightforward problems.

а=-5

a+b=97 ab=997 Could you solve it.🤔

2or3😂

Isn't there a complex solution? 9^x + 3^x = 20 (3^2)^x + 3^x = 20 3^(2 * x) + 3^x = 20 3^(x * 2) + 3^x = 20 (3^x)^2 + 3^x = 20 Let u = 3^x (3^x)^2 + 3^x = 20 => u^2 + u - 20 = 20 - 20 => u^2 + u - 20 = 0 => 1 * u^2 + 1 * u + (-20) = 0 Let a = 1, b = 1, c = -20 1 * u^2 + 1 * u + (-20) = 0 => a * u^2 + b * u + c = 0 u = (-b +/- sqrt[b^2 - 4 * a * c]) / (2 * a) u = (-1 +/- sqrt[1^2 - 4 * 1 * (-20)]) / (2 * 1) u = (-1 +/- sqrt[1 + 80]) / (2) u = (-1 +/- sqrt[81]) / 2 u = (-1 +/- sqrt[9^2]) / 2 u = (-1 +/- 9) / 2 u = (-1 + 9) / 2, or u = (-1 - 9) / 2 u = 8 / 2, or u = -10 / 2 u = 4, or u = -5 Remember, u = 3^x u = 4, or u = -5 => 3^x = 4, or 3^x = -5 Suppose 3^x = 4 3^x = 4 log(3^x) = log(4) x * log(3) = log(4) x * log(3) / log(3) = log(4) / log(3) x * log_3(3) = log_3(4) x * 1 = log_3(2^2) x = 2 * log_3(2) Suppose 3^x = -5 3^x = -5 ln(3^x) = ln(-5) x * ln(3) = ln(-1 * 5) x * ln(3) / ln(3) = ln(-1 * 5) / ln(3) x * log_3(3) = (ln[-1] + ln[5]) / ln(3) x * 1 = ln(-1) / ln(3) + ln(5) / ln(3) x = ln(e^[i * tau / 2]) / ln(3) + log_3(5) x = (i * tau / 2) * ln(e) / ln(3) + log_3(5) x = (i * tau / 2) * 1 / ln(3) + log_3(5) x = i * tau / (2 * ln[3]) + log_3(5) x1 = 2 * log_3(2) x2 = i * tau / (2 * ln[3]) + log_3(5)

Expliquer vous

From equation (1) we get a = 11-b. Insert this into (2) to get (11-b)b = 111 -> 11b - b² = 111 -> b²-11b-111 = 0. Now solve for b1,2 by applying the quadratic formula to get b1 = 33/2 and b2 = -11/2. Insert either solution into equation (1) to find that in case of b1, a1 would become -11/2, while in case of b2, a2 would calculate as 33/2. Hence there are two reciprocal solutions for real numbers of a and b: [a1,b1] = [-11/2,33/2] and [a2,b2] = [33/2,-11/2].

Not meaning to criticize, because I’m sure your videos are valuable for people who are just beginning to understand algebra, but can you occasionally put videos which are more challenging? Thank you.

Where did you get 15?

Excellent. Great job ❤

Thanks mate! :)

let u=3^x , u^2+u-20=0 , (u-4)(u+5)=0 , u= 4 , / -5 < 0 not a solu for x/ 3^x=4 , x=log4/log3 , 1 -4 test 9^x+3^x=16+4 , --> 20 , OK , 5 -20

a + b = 11 a + b - b = 11 - b a = 11 - b ab = 111 (11 - b)b = 111 11b - b^2 = 111 11b - b^2 - 111 = 111 - 111 -b^2 + 11b - 111 = 0 b^2 - 11b + 111 = 0 b = (-[-11] +/- sqrt[(-11)^2 - 4*1*111]) / (2 * 1) b = (11 +/- sqrt[121 - 444]) / (2) b = (11 +/- sqrt[-333]) / 2 b = (11 +/- sqrt[-1 * 3 * 3 * 37]) / 2 b = (11 +/- sqrt[-1] * sqrt[3^2] * sqrt[37]) / 2 b = (11 +/- i * 3 * sqrt[37]) / 2 b = (11 + i * 3 * sqrt[37]) / 2, or b = (11 - i * 3 * sqrt[37]) / 2 b1 = (11 + i * 3 * sqrt[37]) / 2 b2 = (11 - i * 3 * sqrt[37]) / 2 a1 = 11 - b1 a1 = 11 - (11 + i * 3 * sqrt[37]) / 2 a1 = 11 * 2 / 2 - (11 + i * 3 * sqrt[37]) / 2 a1 = 22 / 2 - (11 + i * 3 * sqrt[37]) / 2 a1 = 22 / 2 + (-11 - i * 3 * sqrt[37]) / 2 a1 = ([22 - 11] - i * 3 * sqrt[37]) / 2 a1 = (11 - i * 3 * sqrt[37]) / 2 a2 = 11 - b2 a2 = 11 - (11 - i * 3 * sqrt[37]) / 2 a2 = 11 + (-11 + i * 3 * sqrt[37]) / 2 a2 = 11 * 2 / 2 + (-11 + i * 3 * sqrt[37]) / 2 a2 = 22 / 2 + (-11 + i * 3 * sqrt[37]) / 2 a2 = ([22 - 11] + i * 3 * sqrt[37]) / 2 a2 = (11 + i * 3 * sqrt[37]) / 2 { (a1, b1), (a2, b2) } = { ([11 - i * 3 * sqrt(37)] / 2, [11 + i * 3 * sqrt(37)] / 2), ([11 + i * 3 * sqrt(37)] / 2, [11 - i * 3 * sqrt(37)] / 2) }

subst u^32 = sqrt(x) => u^31= 8 u = 8^(1/31) resubstitution: sqrt(x) = 8^(32/31) x = 8^(64/62) = 8^(32/31)

Trivial try = -5. Finished in 30 s.

Another method.. SQRT(3^x * SQRT( (9^x) * SQRT(81^x ) ) ) = 81 = 3 ^ 4 where SQRT(81 ^ X) = SQRT(9 ^ 2x) = 9^x SQRT( 3^x * SQRT( 9^x * 9^x ) ) = 3 ^ 4 where SQRT( 9^x * 9^x ) ) = 9 ^ x = 3 ^ 2x SQRT( 3 ^ x * 3 ^ 2x ) = 3 ^ 4 SQRT( 3 ^ 3x ) = 3 ^ 4 where SQRT( 3 ^ 3x ) = 3 ^ (3/2)x 3 ^ (3/2)x = 3 ^ 4 where 3x/2 = 4 multiply each side by 2/3. x = 8/3

262143

You still need to verify x2,y2

The answer is Log(φ )/Log(5). I think you have done a mistake somewhere.

(5^x)+(25^x)=125^x [(5³)^x]-[(5²)^x]-(5^x)=0 (5^x)³-(5^x)²-(5^x)=0 Divide by (5^x)≠0: (5^x)²-(5^x)-1=0, a quadratic equation in 5^x: 5^x≠½[1±sqrt(5)] As 5^x can't be negative, 5^x=ß is golden ratio --> x=[log(ß)]/log(5)

What you get are three pairs of real numbers, not of natural number.