
- Видео 58
- Просмотров 64 673
Lewis Mitchell
Добавлен 27 июн 2006
Big Happy: Revealing the Character of Cities Through Data -- Lewis Mitchell at TEDxUVM 2012
(NOTE: This new upload has improved audio; the initial upload had 738 views)
LEWIS MITCHELL
Lewis Mitchell is a a postdoctoral researcher in mathematics and climate. Broadly, he is interested in the messy interface between the "real" world and the more abstract world of mathematics. More specifically, his research is focused in the areas of numerical weather prediction (NWP) and data assimilation, which use techniques from many areas of applied mathematics.
About TEDx
In the spirit of ideas worth spreading, TEDx is a program of local, self-organized events that bring people together to share a TED-like experience. At a TEDx event, TEDTalks video and live speakers combine to spark deep discuss...
LEWIS MITCHELL
Lewis Mitchell is a a postdoctoral researcher in mathematics and climate. Broadly, he is interested in the messy interface between the "real" world and the more abstract world of mathematics. More specifically, his research is focused in the areas of numerical weather prediction (NWP) and data assimilation, which use techniques from many areas of applied mathematics.
About TEDx
In the spirit of ideas worth spreading, TEDx is a program of local, self-organized events that bring people together to share a TED-like experience. At a TEDx event, TEDTalks video and live speakers combine to spark deep discuss...
Просмотров: 39
Видео
Dr Lewis Mitchell: Finalist, Tall Poppy of the Year 2018
Просмотров 532 месяца назад
2018 SA Science Excellence Awards. Dr Lewis Mitchell, Lecturer in Applied Mathematics, The University of Adelaide. For more info visit www.scienceawards.sa.gov.au Original video: ruclips.net/video/_kDZkc1 GU/видео.html
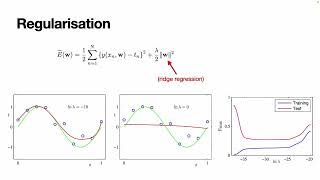
Mathematics of AI: error sources, bias-variance, and regularisation in deep learning (Part II)
Просмотров 85Год назад
Mathematics of AI lecture, largely based on Simon Prince (2023) "Understanding Deep Learning" (udlbook.github.io/udlbook/), Chapters 8 & 9, about double descent and regularisation in deep learning. Also covers some material from the classic textbooks: Goodfellow et al (2016), "Deep Learning: An Introduction" (www.deeplearningbook.org), Chapter 7 on dropout in deep learning, and some examples fr...
Mathematics of AI: error sources, bias-variance, and regularisation in deep learning (Part I)
Просмотров 109Год назад
Mathematics of AI lecture, largely based on Simon Prince (2023) "Understanding Deep Learning" (udlbook.github.io/udlbook/), Chapters 8 & 9, about sources of error (noise, bias, variance) in deep learning, the bias-variance tradeoff and double descent. Lecture given at The University of Adelaide, 22 August 2023. There is a period where I go through some of the mathematics from Ch 8 of Prince (20...
Criminal Machine Learning: Based on "Calling Bullsh*t"
Просмотров 265Год назад
Topic video on criminal machine learning, a modern instance of "garbage in, garbage out". Based on the Bergstrom & West lecture video of the same name: ruclips.net/video/rga2-d1oi30/видео.html For use in teaching at The University of Adelaide.
Garbage in, garbage out: Based on "Calling Bullsh*t"
Просмотров 105Год назад
Topic video on "garbage in, garbage out" in machine learning, based on Bergstrom & West's lecture video: ruclips.net/video/pcmUdXIJQ74/видео.html. For use in teaching courses at The University of Adelaide.
What comes next?
Просмотров 652 года назад
A short summary video, and some explanation about what comes next in the course. NOTE: this was recorded in 2021, and a couple of details are out of date for example, in 2022 the final exam is worth 40%, not 50%, and held in-person rather than online. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
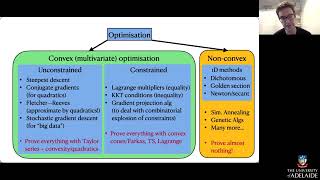
Course summary
Просмотров 3082 года назад
A short summary of the course: constrained and unconstrained convex optimisation, plus a short tour of non-convex optimisation. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Gradient projection algorithm example
Просмотров 6 тыс.2 года назад
Here (at last!) we see how the full gradient projection algorithm works, to find its way to a solution of a constrained optimisation problem. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Completing the gradient projection algorithm
Просмотров 9872 года назад
We need a tiny bit more mathematics to be sure that solutions found by the incomplete gradient projection algorithm satisfy the KKT conditions this gives us the full gradient projection algorithm which we describe in this video. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Incomplete gradient projection in practice
Просмотров 4962 года назад
How the incomplete gradient projection algorithm for solving constrained convex optimisation problems works in practice. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Incomplete gradient projection
Просмотров 6032 года назад
Introduction to how orthogonal projections are used within the incomplete gradient projection algorithm for solving constrained convex optimisation problems in a "greedy" but efficient manner. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Orthogonal directions and gradient projection
Просмотров 7582 года назад
An introduction to the gradient projection algorithm for solving constrained convex optimisation problems. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Variants of the KKT conditions
Просмотров 4032 года назад
This video describes a few different variants of the KKT conditions, for different types of constrained optimisation problems. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
Using KKT conditions to find the minimiser
Просмотров 1 тыс.2 года назад
The theorem about the KKT conditions is all well and good, but how do you use them to actually find the minimiser for a constrained convex optimisation problem? This video explains how this works through some examples. Topic video for APP MTH 3014/4114/7072 Optimisation at The University of Adelaide.
KKT conditions: proof of the main theorem
Просмотров 1,3 тыс.2 года назад
KKT conditions: proof of the main theorem
Karush-Kuhn-Tucker (KKT) conditions: motivation and theorem
Просмотров 6 тыс.2 года назад
Karush-Kuhn-Tucker (KKT) conditions: motivation and theorem
Lagrange multipliers: optimisation with equality constraints
Просмотров 9812 года назад
Lagrange multipliers: optimisation with equality constraints
Constrained convex optimisation: Introduction
Просмотров 3662 года назад
Constrained convex optimisation: Introduction
Stochastic gradient descent: computation time analysis
Просмотров 2222 года назад
Stochastic gradient descent: computation time analysis
Stochastic gradient descent: a most basic example
Просмотров 2792 года назад
Stochastic gradient descent: a most basic example
Stochastic gradient descent: an introduction
Просмотров 3662 года назад
Stochastic gradient descent: an introduction
Conjugate gradient method: comments and limitations
Просмотров 5332 года назад
Conjugate gradient method: comments and limitations
The conjugate gradient method completes in n steps
Просмотров 7892 года назад
The conjugate gradient method completes in n steps
Conjugate directions: definition and properties
Просмотров 1,6 тыс.2 года назад
Conjugate directions: definition and properties
Convergence of steepest descent on quadratic functions
Просмотров 8532 года назад
Convergence of steepest descent on quadratic functions







thanks
Thank you for this! Where can one find the book(lectures) you use for the explanation?
Dividing the learning rate by two works better. However I divide the learning rate by two until it is very small and will then take the step anyway. If I make a successful step then I multiply the learning rate by 4 not to exceed the original learning rate. This way the learning rate adapts to the terrain which rarely like a bowl in reality.
Thank you. where can i get more video on algebra cones
x es semipositive in the convex cone section
Great explanation! Using a 2D explanation makes it so much easier to visualise and understand! Thanks!
Thank you so much, I now have a clear geometric intuition in my head!
Nice explanation!
God i hate this type of math the most. Why must I learn this why lord why.
Many thanks for your clear explanation. Just a minor correction: Almost at the end of the lecture, it should be noted that the column space of the transpose of matrix M is orthogonal to the null space of matrix M.
7:34
i was loong for dichotomous search for c language but this shit is good too
Oh thank you from Vietnam !
Thanks for your video. I think this series is being underestimated since you may quickly understand what the algorithm does without any prior knowledge like Krylov space.
Great video. Thank you
I have a doubt. It is mentioned in the video that for 2 constraints, there are four things to check. I understood that we are looking for the solution on the boundaries of the contraint set where at least one of the constraints are active. But the optimum solution can be a point in the interior of the constraint set where no constraints are active. How will I get the internal optimum point with unconstraint optimization technique?
It's just the condition of stationary, simple derivative (Gradient ) of the function with constraints.
Its been months searching for it please send me a matlab code for this
I need a matlab code of that please
How much iterations it will take, I mean is there fixed number of iteration like conjugate gradient.
Hello dear prof. Mitchell. I went through this lecture and noticed that constraint minimiser x* = (1, 2) is the solution closest to the unconstraint minimiser x*_uncontraint =(0,5). Is that a coincidence or is there some rule of thumb in this?
Awesome video. Thank you!
Cool lecture! May I ask what's the reference text are you using? Thanks and keep it up
Me puedes compartir la presentación???
hi, may i know what 'k mod n' means and n stands for what?
bit late, but k mod n is the remainder left when n divides k. In this algorithm, the consequence of this is that if the algorithm has not converged in n steps (as it ideally would), the new search direction is taken to be the direction of steepest descent.
Superb, thanks for the clarity
Thanks!!
Could you explain why y is in R(M^T) I thought the R(M^T) is the same as N(M) = S
This is the definition of a column space: y is in the column space of M transpose, which is orthogonal to the null space of M.