
- Видео 35
- Просмотров 55 149
Small Universe
Добавлен 3 дек 2022
Math Olympiad Problems : Solving Equations in TWO Different Ways
Hi, I'll show you how you can solve a math olympiad problem, that is, how to solve equations in two different ways. I hope you have fun watching.
#math , #smalluniverse, #how
#math , #smalluniverse, #how
Просмотров: 49
Видео
Math Olympiad Problem: Nice Algebra Challenge and The Golden Ratio
Просмотров 13Год назад
Hi, in today video I'll show you a nice math olympiad problem where you will solve a nice algebra challenge and get golden ratio. The golden ratio, also known as the divine proportion, is a mathematical concept that describes the relationship between two quantities where the ratio of the smaller quantity to the larger quantity is the same as the ratio of the larger quantity to the sum of the tw...
Math Olympiad Problems: Fun Algebra Challenge
Просмотров 50Год назад
Hi, I'll show you a cool math olympiad problem, and it's solution. We'll be solving an equation using logarithms. You'll also see how useful logarithms can be. A logarithm is the inverse function of an exponentiation. For example, if we have 2^3 = 8, then the logarithm of 8 to base 2 is 3. In general, the logarithm of a number b to base x is denoted as log_x(b) and is defined as the exponent to...
Math Olympiad Problem: Nice Algebra Challenge
Просмотров 13Год назад
Hi, in today's video I'll show you a cool math olympiad problem with a nice algebra challenge. Hopefully you'll like it. It's an algebra problem that can be a little bit challenging, but it's worth it. #math, #smalluniverse, #how
Math Problems: Prove Trigonometric Identity With Integrals
Просмотров 18Год назад
HI, in today's video I'll show you how you can prove trigonometric identity with integrals and derivatives. This is an easy problem that you too can do. You can also try to prove other trigonometric identities, just pick a trigonometric identity and play with id. Thanks for watching.
Math Olympiad Problems: A Nice Algebra Challenge
Просмотров 16Год назад
Hi, in this video I'll show you how to solve an easy math problem. This is a typical problem that you can encounter anywhere in math. Solving equations, even difficult ones, can teach you some fundamental principles in mathematics. I hope you had fun watching this video. #maths, #SmallUniverse, #olympiad
Math Olympiad Problems: Solving Systems of Equations
Просмотров 24Год назад
Math Olympiad problem: solving systems of equations In this video, we'll be learning how to solve systems of equations. This is a common problem on the math Olympiad and it's a required skill for students who hope to achieve success on the math Olympiad. Solving systems of equations is a skillset that's important for students in all areas of mathematics. By learning how to solve systems of equa...
Math Olympiad Problems and Solutions : Solving Equations
Просмотров 8Год назад
Math Olympiad Problems and Solutions : Solving Equations
Math Problems and Solutions : Solve This Expression Without a Calculator
Просмотров 3Год назад
Math Problems and Solutions : Solve This Expression Without a Calculator
Math Problems and Solutions : Decompose Polynomial Fractions
Просмотров 37Год назад
Math Problems and Solutions : Decompose Polynomial Fractions
Solving Gaussian Integral Using Polar Coordinates
Просмотров 1102 года назад
Solving Gaussian Integral Using Polar Coordinates
ChatGPT Programming Using 3Blue1Brown's Manim
Просмотров 6 тыс.2 года назад
ChatGPT Programming Using 3Blue1Brown's Manim
How To Quickly And Easily Solve Equations
Просмотров 262 года назад
How To Quickly And Easily Solve Equations
Relaxing music for learning and resting
Просмотров 162 года назад
Relaxing music for learning and resting


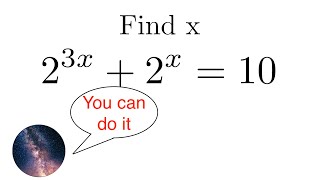






Not invisible at all !
ruclips.net/user/shortsvfpxHh6EHGA?si=eAibR-nCliU5paaO
How did you use Manim
e^-x² dx not dx e^-x²
Thanks Man
What software do you use to make these written animations ?
Soo cursed 💀💀💀
my goodness why is it ʃdx.e^-x²
Thanks dude! Will try this
When i plug it into desmos anything i insert at the top of the integral bigger then 43 it makes it freak out and gives me weird values
What was that partial derivative determinant thing when you said r^2 = x^2+y^2?
that’s called the jacobian, it accounts for the change between coordinate systems (cartesian -> polar in this case). you’ll learn about it in calc 3
@@kathode1 I learned about it within the next few days after that 😁 Then there was even some guy named Jordan who apparently had a lemma
Who tf puts the dx like that. It's almost like the dx closed the integral
Thanks man
I legitimately shed tears everytime I try to learn math
A thousand likes! Good job!
Yea, this is why I stopped at calculus 1.
This is merely the preface for multiple integral of calc 3. The whole calculus is a baby stuff
@@spiderjerusalem4009 🤓
0:08
Dx in front nooo
copy paste eh ???
Ok, but how: 0:08 why is there a matrix 😭
@@danialjeelani but those are vector based? Is there supposed to be vectors in the Gaussian integral
@@BlueMushroomSmurfCatkinda, you're transforming the integral from R->R to R²->R. I wouldn't call them vectors (they are still outputting a scalar number), but there is a vectorial explanation of what is going on there
from what I understand, because you're transforming space from the xy basis to the rθ basis, and because you can interpret differential forms as covector fields, they transform with the Jacobian, which is the determinant of that matrix
@@BlueMushroomSmurfCat 𝐫:uv-plane → xy-plane 𝐫(u,v)=(x,y,0) 𝝏ᵤ𝐫 Δᵤ ≈ 𝐫(u+Δᵤ,v)-𝐫(u,v) 𝝏ᵥ𝐫 Δᵥ ≈ 𝐫(u,v+Δᵥ)-𝐫(u,v) (Δᵤ,Δᵥ)→(0,0) 𝐫ᵤ = 𝝏ᵤ𝐫 = (𝝏ᵤx, 𝝏ᵤy, 0) 𝐫ᵥ = 𝝏ᵥ𝐫 = (𝝏ᵥx, 𝝏ᵥy, 0) Although cross products do only work in three dimension, we can extend those elements to have them lie on the plane z=0 Area = Sum of norm of cross products of 2 infinitesmall vectors, one of which goes in u-direction, whilst the other in v-direction = 𝜮 ||[𝐫(u+Δᵤ,v)-𝐫(u,v)]×[𝐫(u,v+Δᵥ)-𝐫(u,v)]|| (Δᵤ,Δᵥ)→(0,0) = 𝜮 ||(𝝏ᵤ𝐫 Δᵤ)×(𝝏ᵥ𝐫 Δᵥ)|| (Δᵤ,Δᵥ)→(0,0) = 𝜮 ||𝝏ᵤ𝐫 ×𝝏ᵥ𝐫|| |ΔᵤΔᵥ| (Δᵤ,Δᵥ)→(0,0) = 𝜮 |Δx Δy|, (Δx,Δy)→(0,0) whence Area = ∫ dA = ∫∫ dxdy = ∫∫ ||𝐫ᵤ×𝐫ᵥ|| dudv hence the imposition that dxdy = ||𝐫ᵤ×𝐫ᵥ|| dudv = |det((xᵤ,xᵥ),(yᵤ,yᵥ))| du dv
The Jacobian is just the first-order derivative for functions f : R^n -> R^m
Thanks man! you rock brother!
They're less complex ways to find the solution
Yep
This is actually the easiest. Nothing else works. Not u sub, trig sub, integration with parts. You could try this using Laplace transform but then again, why keep a table of Laplace transformations at all times
@@TheHellBoy05 yes, using polar coordinates sub for double integrals
@@silveykmbro, that is what the jacobian does
@@TheHellBoy05Feyman technique could do. Laplace solved it too (reference to the person, not his transformation. Bprp covered it)
NameError: name 'FRAME_WIDTH' is not defined every single time
so edgy
WHO THE FUCK PUTS THE DX IN FRONT
wouldn't it make sense to pin your version of manim in "my-manim-environment" to the one that was released as of 2021? (assuming that ChatGPT when trained was using the latest version of manim at the time)
Thanks! Didn't know that was possible. "pip uninstall manim" and "pip install manim==0.11.0" worked well for me
Thx for help me!
wtf is that
the gaussian integral, its just the normal distribution mean 0 sd 1 being integrated to infinity, comes out as sqrt(pi)
@@_mekk_ ah right thx mate
@the brain yea np, there's a nice video that explains it rather simply using polar coordinates, the premise is that the definite integral from 0-♾️ of e^-x^2 is = to 0-♾️ of e^-y^2 so u can then change it into double integral of e^-(y^2+x^2) and then u can draw it in 3d and find it using tubes and simple geometry and a simple improper integral
Just opening to calc 3 regarding multiple integrals. Nothing hard, notably if you're already into gamma/beta function
@spiderjerusalem4009 yeah im not american so i dont know what calc 3 is, but actually in my own time i found a way of doing this with volumes of revolutions rather that whatever the fuck this is and actually it turned out pretty nice. I also have no idea what the gamma or beta functions are, do you cover that at university?
Y is the dx in front:((
Gross physicist notation, it hurts the eyes
because he deserves hell
Leibniz thats why
Weird preference
Don’t worry, you only have to integrate 1 from -inf to inf and multiply it by “e^-x^2”!!!
You have to ask more specific requests from the AI. For example, you should ask the AI to draw the object near the center of the screen. You could also ask for the dots to be linear horizontally, and that the left dot should be connected to the center dot, and the center dot connected to the right dot. The more you put in, the more you'll get out. It's AI, not telepathic 😉
hello can you plz tell me what software do you use to make this video is it manim ?
Yes, it is manim
:OO OMG --------•---- 1:37 IQ 100
Like, Share or Subscribe if you want.
Like, Share or Subscribe (if you want)