
- Видео 524
- Просмотров 118 298
wisfrank
Добавлен 18 апр 2023
Harvard University Admission interview Tricks
Harvard University Admission interview Tricks
Просмотров: 0
Видео
A Very tricky Cambridge University Admission algebra exam | entrance aptitude Test.
Просмотров 4719 часов назад
A Very tricky Cambridge University Admission algebra exam | entrance aptitude Test.
Maths Olympiad | How to solve for X & Y in this equation
Просмотров 432 часа назад
Maths Olympiad | How to solve for X & Y in this equation
Germany | Maths Olympaid | let's solve this in a beautiful way
Просмотров 1204 часа назад
Germany | Maths Olympaid | let's solve this in a beautiful way
Germany | Maths Olympaid | let's solve this in a beautiful way
Просмотров 5997 часов назад
Germany | Maths Olympaid | let's solve this in a beautiful way
Germany | Maths Olympaid | can you solve this
Просмотров 1669 часов назад
Germany | Maths Olympaid | can you solve this
Germany | Maths Olympaid | can you solve this
Просмотров 429 часов назад
Germany | Maths Olympaid | can you solve this
Germany | Maths Olympaid | can you solve this
Просмотров 30912 часов назад
Germany | Maths Olympaid | can you solve this
Germany | Maths Olympiad Exponential Equation | solve for the value of X
Просмотров 1,6 тыс.14 часов назад
Germany | Maths Olympiad Exponential Equation | solve for the value of X
Germany | Maths Olympaid | can you solve this
Просмотров 72016 часов назад
Germany | Maths Olympaid | can you solve this
Word Problem | Find the numbers in the statement
Просмотров 5119 часов назад
Word Problem | Find the numbers in the statement
Harvard University Admission Entrance interview Tricks
Просмотров 36521 час назад
Harvard University Admission Entrance interview Tricks
A Nice Algebra Problem Solving: Find the value of X in the equation|important Olympiad questions
Просмотров 218День назад
A Nice Algebra Problem Solving: Find the value of X in the equation|important Olympiad questions
A Nice Olympiad Exponential Maths Problem
Просмотров 494День назад
A Nice Olympiad Exponential Maths Problem
Germany maths Olympiad Exponential Equation | maths important questions
Просмотров 268День назад
Germany maths Olympiad Exponential Equation | maths important questions
A Nice Maths Olympiad Exponential Equation | The Six solution
Просмотров 329День назад
A Nice Maths Olympiad Exponential Equation | The Six solution
Germany Olympiad Exponential Equation | How can we solve this? | maths important questions
Просмотров 1,1 тыс.14 дней назад
Germany Olympiad Exponential Equation | How can we solve this? | maths important questions
A Nice Radical Equation | Maths Olympiad Question
Просмотров 24814 дней назад
A Nice Radical Equation | Maths Olympiad Question
A Nice Exponential Equation | Maths important question.
Просмотров 3414 дней назад
A Nice Exponential Equation | Maths important question.
Very Nice Olympiad Maths Exponential Equation | Maths important question
Просмотров 28614 дней назад
Very Nice Olympiad Maths Exponential Equation | Maths important question
A Nice Algebra Olympiad equation| Maths important question | similar to Olympiad maths
Просмотров 4014 дней назад
A Nice Algebra Olympiad equation| Maths important question | similar to Olympiad maths
Japanese Maths Olympiad Algebra Equation | Maths important question | similar to Olympiad maths
Просмотров 53014 дней назад
Japanese Maths Olympiad Algebra Equation | Maths important question | similar to Olympiad maths
Germany maths Olympiad Exponential Question | Maths important question | similar to Olympiad maths.
Просмотров 91321 день назад
Germany maths Olympiad Exponential Question | Maths important question | similar to Olympiad maths.
Harvard University Admission Entrance Tricks | Maths important question | similar to Olympiad maths
Просмотров 2,4 тыс.21 день назад
Harvard University Admission Entrance Tricks | Maths important question | similar to Olympiad maths
Harvard University Admission Entrance Tricks | Maths important question | similar to Olympiad maths
Просмотров 1,2 тыс.21 день назад
Harvard University Admission Entrance Tricks | Maths important question | similar to Olympiad maths
Harvard University Admission Entrance Exam | maths important questions.
Просмотров 13921 день назад
Harvard University Admission Entrance Exam | maths important questions.
Harvard University Admission interview Tricks | maths important questions.
Просмотров 20721 день назад
Harvard University Admission interview Tricks | maths important questions.
Harvard University Admission interview Tricks | Similar to Olympiad maths | maths important question
Просмотров 12121 день назад
Harvard University Admission interview Tricks | Similar to Olympiad maths | maths important question
Harvard University Admission interview Tricks | Find the value of K? | maths important questions
Просмотров 55528 дней назад
Harvard University Admission interview Tricks | Find the value of K? | maths important questions
A nice exponential algebraic equation | Olympiad Maths | maths important questions
Просмотров 15128 дней назад
A nice exponential algebraic equation | Olympiad Maths | maths important questions


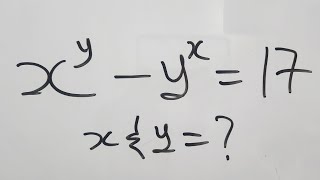
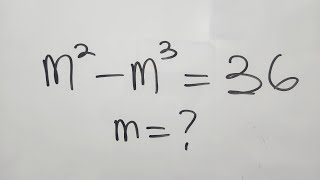

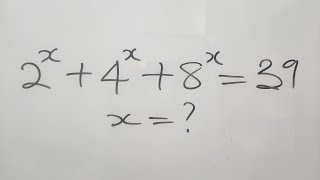

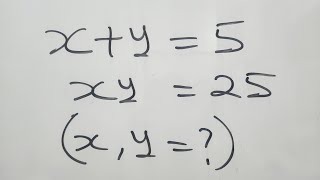

👍
Thanks
We solve for x first, second we solve for y to thrid plog the values on the equations...
You are right
You solved it the difficult way😅
Pls can you show us the easiest way
@wisfrank-zc6yp guessing
Great work. Thanks
Glad you liked it!
Awesome!!!!
Thank you! Cheers!
What's about factorizing 16^4 out and have 16^4(16-1)
There are different ways to arrive at the answer, the one you are familiar with is what you can use
Arigato gozaimasu. You have given me more confidence
Thank you, that is maths it is just the application of rules
y=-i*sqrt(8). To solve you have to take sqrt(y) as c+id, where c and d are real values and i=sqrt(-1)
You are on the right path, that's right
@@wisfrank-zc6yp More simple. If we take a square of both parts we get 2iy = 16.
I started with dividing by 5^x and ended up with 5^2x-5^x-1=0 solving to log base 5 (-1+sqrt(5)/2) any idea why i got root 5 instead?
You need to apply the rule you understand, but many thanks
This is a 30sec problem without pen and paper. Your method is way too complicated. And there is only one solution, not two.
Your opinion is valid, but in this tutorial we need to give all the explanation so that everyone will understand all the steps,.
Je ne comprends pas anglais mais j'ai tout compris très bon professeur
Thank you very much
The fact that this takes more than two lines eludes me. Twice 5^k = 100, 5^k = 50, k = log5(50). The end...
You correct tho, but what of some people that don't understand the way you do, I could solve it more short than that but we need to give more explanation for others that don't have such knowledge.
Too long
That is the full explanation
at 1:42 where you cancelled out the square root and the raised to the second power, shoudn't you have taken the absolute value of what was under the square root, leaving you with y instead of -y?
(Sqrt-y)^2, here the power of 2 will cancel the sqrt leaving only -y
that was really smart, can you make more videos with problems that use difference/sum of two cubes?
Ok,
Solution: f(x) = f(x+3-3) = (x-3)²+3*(x-3)+2 = x²-6x+9+3x-9+2 = x²-3x+2 Checking the result: f(x+3) = (x+3)²-3*(x+3)+2 = x²+6x+9-3x-9+2 = x²+3x+2 everything o.k.
You are on the right track, many thanks.
How did you obtain the square root of -1 in your first application of square root?
Square of -1 is iota which equal to i
@wisfrank-zc6yp I don't understand how you got -1 when you were finding the square of -4 .
-4= 4x-1, root4=2 and root -1 =iota i
Great but I think your "Note" at the end has an error in the explanation. Your 2^ log(3) base(2) does not match a^ log(a) base(b)
Yes you are right, I saw it myself
Is this really necessary ?
Yes it does
I want to be a great mathematician.
What you need to do is to study continuously and know maths rules
wow ok got it
Yes, just a simple step by step
X Is 2
Correct
But in exams One had less than a minute to solve this without a calculator 😂
You know, in this context, we give you everything for you to understand. If it were to be an exam, there are steps I would not go through
Nice
Yes sir
Guru!! I hail u oo
Thank you sir
Simplified?
Thanks for your support, I really appreciate
great explanation! i enjoyed it very much.
Glad you liked it!
that was a really good video i enjoyed it thank you
I'm glad to hear it! Thanks for your support.
how do you input the lambert w function into the lambert w function into the calculator?
Not all calculator has this function
😂😂😂 i cant make it one of difficult math problem ever
All what you need is understanding the steps which is well explained
what if you meet it for the first time..would you reach those steps?
Mathematics is all about application of rules to arrive at the answer
You can't do all these in an interview. An easy method is expected from the student. The quicker way is to list the 6th roots of the complex number z=2^6. Which are 2e^{ipik/3} for k=0,1,...,5
You when you have a constant to the power of 6, the answers are 6, so doing the student should understand how to solve this first before looking for a shortage way.
fair enough
Thanks for your support
Why not simply writing : Sqrt(x) = 2 - Sqrt(2) . So (Sqrt(x))^2 = (2-Sqrt(2))^2 and x = 4+2-4Sqrt(2) = 6-4Sqrt(2)
You are correct though
I got lost a bit in the middle but then when you were wrapping up it just clicked. Cool problem
Is always good to follow up little by little
super ! thank you
😊😊😊Thank you too!
You are welcome
There is only 1 correct answer that is X2 (X1 is not the correct one but it formed from the "square both side" method)
X2 = 6-4Sqrt(2) = 2+4-2Sqrt(2)Sqrt(4)= (2-Sqrt(2))^2 so Sqrt (X2) = 2-Sqrt(2) substitute back and get 2 X1 = 6+4Sqrt(2) = 2+4+2Sqrt(2)Sqrt(4)=(2+Sqrt(2))^2 so Sqrt (X1) = 2+Sqrt(2) substitute back and get 2+2Sqrt(2) (X1 is not the correct answer) By the way, Nice question!
You are correct, only one answer is correct@fame-ht4ex
@@fame-ht4ex Perhaps a nice question, but a stupid demonstration from wisfrank. As said by a german proverb "Warum es einfach machen, wenn kompliziert auch geht".
nice !
Thank you! Cheers!
Lovely maths… because nude girls are not here twerking people are not interested 😊
You are correct though
Man, you are so stupid
27; 1,1508... .
27 is the correct answer
@@wisfrank-zc6yp The equation has 2 roots. Check.
It has one root, only quadratic equation has 2 roots, this is not a quadratic Equation @Misha-g3b
You are wrong, and I said to check up for 1.1508... . @@wisfrank-zc6yp
@@wisfrank-zc6ypYou are wrong, and l said to check up for x=1.1508... .
Simple rootx = 2 - root2 X = (2-root2)2 X = 4+2-4root2 X = 6-4root2
This is excellent
2(3-2V2).
Pls give us more details
@@wisfrank-zc6yp About what?
Good video! One thing though, by squaring both sides two times you introduced an extraneous solution, namely 6 + 4*sqrt(2). To show this, you can write 6 + 4*sqrt(2) as 4 + 4*sqrt(2) + 2, which is precisely (2 + sqrt(2))^2. If you plug this solution in the original equation, this happens: sqrt(2) + sqrt((2 + sqrt(2))^2) = 2 sqrt(2) + 2 + sqrt(2) = 2 2*sqrt(2) = 0 sqrt(2) = 0 (absurd) Notice that you can do the same process with 6 - 4*sqrt(2) to show that it is in fact a solution to the original equation: 6 - 4*sqrt(2) = 4 + 4*sqrt(2) + 2 = (2 - sqrt(2))^2 sqrt(2) + sqrt((2 - sqrt(2))^2) = 2 sqrt(2) + 2 - sqrt(2) = 2 2 = 2 I found this out because I tried this problem for myself and this is how I did it: sqrt(2) + sqrt(x) = 2 sqrt(x) = 2 - sqrt(2) By squaring both sides you get: x = 4 - 4*sqrt(2) + 2 x = 6 - 4*sqrt(2) Hope this helps and my explaination is clear, keep up the good work!
Yessssss, you are correct. ❤
why you didn't subtract sqrt2 from both sides and then squared the equation? and also you need to check your answers because one of them in not right. The plus one solution is not right
Pls which one is not correct, can you expatriate for us to see, thanks
@@wisfrank-zc6yp 6+4sqrt2
I like your helmet !
Thank you very much
Thanks 🙂
You are welcome
Excellent clear & concise demonstration ! Thanks for sharing ……..😉
Thanks for watching and subscribing
cubic equations have 3 roots.
Yes but two of them are complex numbers in this case and he's looking for real solutions. So he didn't bother calculating them.
@@DerekRoss1958 I guess I heard him wrong, he seemed to reject the imaginary one.
Well, sometimes you want the imaginary solutions; sometimes you don't. I guess he didn't this time.
I rejected the imaginary one because it does not have real root, the question says all the answers must be real root
You are correct
Great video!
Thanks you very much