
- Видео 39
- Просмотров 277 278
Graph Theory for Educators
Добавлен 19 янв 2016
An introduction to graph theory for high-school educators or hobbyists. The videos on this channel focus on exposing the viewer to concepts in graph theory without including a lot of rigor or detail. I recommend that you view these videos with a textbook or two handy in case you would like more detail on the discussed topics.
Welcome video
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Просмотров: 954
Видео
Face Coloring and Flows - 38
Просмотров 8508 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
More on Flows - 37
Просмотров 5198 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Introduction to Flows - 36
Просмотров 6948 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
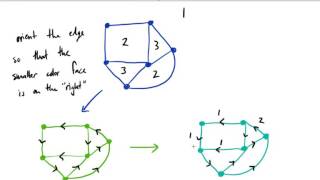
Face Coloring - 35
Просмотров 1,9 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
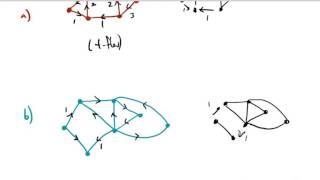
Edge Coloring - 34
Просмотров 16 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Hall's Theorem - 33
Просмотров 82 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Excluded Minors for Outerplanar Graphs - 32
Просмотров 1,9 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Outerplanar Graphs - 31
Просмотров 6 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Euler Characteristic (non planar) - 30
Просмотров 1,6 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Euler Characteristic (planar) - 29
Просмотров 8008 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Graphs on the Torus - 28
Просмотров 5 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Intro to Surfaces - 27
Просмотров 9768 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
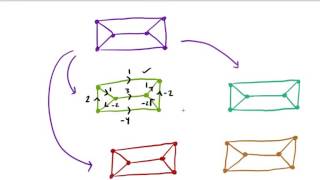
Dual Graphs - 26
Просмотров 49 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.
Planar Graphs - 25
Просмотров 1,3 тыс.8 лет назад
This video was made for educational purposes. It may be used as such after obtaining written permission from the author.






Hey mate, cheers for the video. You've explained it really well for me to undestand it.
awesome clear and simple explanation !!! understood the proof😀
This was so concise! Thanks for showing actual examples :D
How did I get here? 😂❤
thanks!
What can one do with all of this then? Is this just theoretical mathematics?
34
Thank you❤
Good work man. Thanks.
chup kr chobu
wow what a good explanation, u made that sound so easy, Thanks!
great explanation
Thank you very much, this explanation make so much sense and explains every detail
wow!! Great explanation
Suppose we contract 2 vertices v2 and v3 and then if we delete vertex v2 then what will happen? Only v2 will be deleted or v2 with all the edges associated with it will be deleted. Kindly answer asap...
Thank you so much. The only lesson on internet where maximum non separable term was described clearly.
Love from kerala✨️
Merci beaucoup tu me sauve la vie
Thank you sir, .... from India😃😃😃
It is very to find out that.. Is a diagraph eulerian or not.. It is theorem that you can find easy.. The statement of theorem is.. A diagraph is eulerian iff each vertex of it has same Indegree and outdegree.
Can I have your mail please,? Can you recommend some a good references for graph theory?
I'm not the creator of the series, but I use West's Introduction to Graph Theory Second Edition when I teach Graph Theory.
Very good explanation, thank you sir!
I’ve rarely seen such a good and concise explanation. Thanks a lot!
Thanks alot for that very helpfull clip
Is there a graph with degrees 3, 3, 3, 3, 3, 5, 5, 6, 6, 6, 6? true or false
false
That's help a lot thank u
thank you so much <3
Thank Sir
another min max relationship I can think of is König’s theorem for bipartite graph.
Nice examples and explanation. Thanks!
Sir can you make playlist of each topic..it may be easier for us to access the content
I understood but its hard to find counter examples sometimes
Thanks!!!
what is the theorem name?
Havel-Hakimi theorem
Very helpful to me. I was looking for such videos. Can you please upload some more about graphs on surfaces and the genus stuff ?
this is a great explanation :) the theorem should say ... iff it contains no subgraph that is a subdivision of K4 or K2,3 though
Can u plz make a video on theorem every tournament has a directed Hamiltonian path
Great video.. very intuitive. Thanks
Thanks
Great video! Just a slight error in 7:50 , 4-6+4 = 2 not -2
Thank you, very helpful
great explanation, thank you
Thanks! This was GREAT!
can one count equivalence classes in advance ?
Should we apply the theorem used in Video 4 and 5 to determine whether a sequence is graphical? I ask because a comment on video 4 stated the sequence s:{3,3,3,1} is not graphical, yet the theorem used in video 4 can be used to illustrate this sequence as graphical, but video 5 doesn't allow it to be simple graphical.
Well, that was easy. Graph Theory for Educators? Looks like my Educators need this video! Thank you Jessie!
thank you very much, that helped
can you post about ford fulkerson method
WoW. Wee need more of this. Sadly i can not send private messages because i have some questions. So how can i ask you smth?
But how do we know v1,v2, v3, v4 existed as a path in the first place?
this video made the concept very clear to me. thanks!