
- Видео 237
- Просмотров 10 990
Zach's Math Zone
Добавлен 27 окт 2024
This channel provides math educational videos that can help anyone learn any topic in math.
How to Find the Equation of a Perpendicular Bisector
In this video I explain how to find the equation of a perpendicular bisector, including a step-by-step example.
Thanks for watching! Be sure to like and subscribe if you enjoyed the video.
You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
Thanks for watching! Be sure to like and subscribe if you enjoyed the video.
You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
Просмотров: 3
Видео
The Angle Addition Postulate With Examples
Просмотров 52 часа назад
In this video I provide an explanation of the angle addition postulate, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Find Area of Circle Given the Diameter
Просмотров 22 часа назад
In this video I explain how to find the area of a circle given the diameter, including an example. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Find Radius of Circle Given the Area
Просмотров 202 часа назад
In this video I explain how to find the radius of a circle given the area, including an example. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
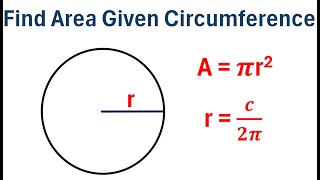
How to Find Area of Circle Given the Circumference
Просмотров 44 часа назад
In this video I explain how to find the area of a circle given the circumference, including an example. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Check if Three Points Are Collinear
Просмотров 154 часа назад
In this video I explain how to check if three points are collinear, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Find Diameter of Circle Given the Area
Просмотров 204 часа назад
In this video I explain how to find the diameter of a circle given the area, including a step-by-step example. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
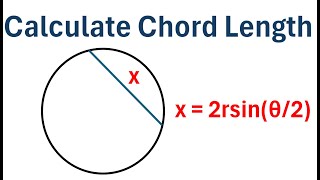
How to Calculate Chord Length in a Circle
Просмотров 324 часа назад
In this video I explain how to calculate the chord length in a circle, including a step-by-step example. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Convert Base 10 to Base 4
Просмотров 77 часов назад
In this video I explain how to convert base 10 numbers to base 4 numbers, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Convert Base 3 to Base 10
Просмотров 127 часов назад
In this video I explain how to convert base 3 numbers to base 10 numbers, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Convert Base 10 to Base 5
Просмотров 97 часов назад
In this video I explain how to convert base 10 numbers to base 5 numbers, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Convert Base 5 to Base 10
Просмотров 157 часов назад
In this video I explain how to convert base 5 numbers to base 10 numbers, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Divide Numbers in Base 5
Просмотров 107 часов назад
In this video I explain how to divide numbers in base 5, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Multiply Numbers in Base 5
Просмотров 147 часов назад
In this video I explain how to multiply numbers in base 5, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.
How to Subtract Numbers in Base 5
Просмотров 57 часов назад
In this video I explain how to subtract numbers in base 5, including several examples. Thanks for watching! Be sure to like and subscribe if you enjoyed the video. You can also send me an email at zachsmathzone@gmail.com with any questions or comments.







A^2/(C-B)=B+C 3^2/1=B+(B+1)=4+5 But 6^2/2=B+(B+1)=18=8+10 does. 5^2/1=25=B+(B+1)=12+13 But 7^2/1=49=B+(B+1)=24+25
Nice circle!
Pivot entrie should be other than 1 in 3rd row how it's possible in row echelon form leading entry is 1 you wrote -4 plz explain this point
Some textbooks define "row echelon form" as having all 1's as pivot entries while others do not. I typically do not consider row echelon form to need 1's as pivot entries. However, *reduced* row echelon form does require that all pivot entries be equal to 1.
Pls do some more problems of eigen values
4.1 x 4.1 = 16.81 4.2 x 4.2 = 17.64 4.125 x 4.125 =17.0156 4.1245 x 4.1245 = 17.0115 4.123 x 4.123 = 16.999 √17 is about 4.123
FYI the doubling the value and using that as the denominator, is just taking the second value of the continued fraction. Also can be found via newton's method.
Great 🎉
Learned this 50 years ago in high school... never had occasion to use it in the real world. However, I did have occasion to use matrix math to do non-linear regression a couple of times about 10 years later. (Imagine storing thermocouple tables in just 5 or 6 floats!) I was never very good at the hand calculations, but I was great at coding it in C. Worked just fine! :)
Thank you for the explanation
You're very welcome!
Isn't this just a single pass of Newton"s method?
5+3+2+1/2+3/5+1/4 = 10+3/4+3/5 = 10+(15+12)/20 = 10+(20+7)/20 = 11+7/20
about 5+3+2+10/20+12/20+5/20+=11 7/20 or 11 1/4 1/1O with a pencil....?
i i captain. >>;=) Been so long since I fooled with these, but thankfully it comes right back. Like in √-90, or i√90, you know 9*10 for instance; if you know your squares, then you know the 9 is 3² and you can steal the 3 out and leave that 10 behind. It may not stand out so obviously with most numbers though, but can cut down on the amt of factorization you have to do. Full factorization of course guarantees you don't miss anything. Pulling out 2s is quick if you can see the last 2 digits of a # is div by 4.
Why we subtract 1 and add 1later in finding n ??
The formula to find the total number of terms is: (number on top of sigma symbol) - (number on bottom of sigma symbol) + 1. Thus, in the first example, the total number of terms is (15) - (1) + 1
@ZachsMathZone thank you
Many people wonder why radians do not appear when we have radians*meters (rad • m). Here is an attempt at an explanation: Let s denote the length of an arc of a circle whose radius measures r. If the arc subtends an angle measuring β = n°, we can pose a rule of three: 360° _______ 2 • 𝜋 • r n° _______ s Then s = (n° / 360°) • 2 • 𝜋 • r If β = 180° (which means that n = 180, the number of degrees), then s = (180° / 360°) • 2 • 𝜋 • r The units "degrees" cancel out and the result is s = (1 / 2) • 2 • 𝜋 • r s = 𝜋 • r that is, half of the circumference 2 • 𝜋 • r. If the arc subtends an angle measuring β = θ rad, we can pose a rule of three: 2 • 𝜋 rad _______ 2 • 𝜋 • r θ rad _______ s Then s = (θ rad / 2 • 𝜋 rad) • 2 • 𝜋 • r If β = 𝜋 rad (which means that θ = 𝜋, the number of radians), then s = (𝜋 rad / 2 • 𝜋 rad) • 2 • 𝜋 • r The units "radians" cancel out and the result is s = (1 / 2) • 2 • 𝜋 • r s = 𝜋 • r that is, half of the circumference 2 • 𝜋 • r. If we take the formula with the angles measured in radians, we can simplify s = (θ rad / 2 • 𝜋 rad) • 2 • 𝜋 • r s = θ • r where θ denotes the "number of radians" (it does not have the unit "rad"). θ = β / (1 rad) and θ is a dimensionless variable [rad/rad = 1]. However, many consider θ to denote the measure of the angle and for the example believe that θ = 𝜋 rad and radians*meter results in meters rad • m = m since, according to them, the radian is a dimensionless unit. This solves the problem of units for them and, as it has served them for a long time, they see no need to change it. But the truth is that the solution is simpler, what they have to take into account is the meaning of the variables that appear in the formulas, i.e. θ is just the number of radians without the unit rad. Mathematics and Physics textbooks state that s = θ • r and then θ = s / r It seems that this formula led to the error of believing that 1 rad = 1 m/m = 1 and that the radian is a dimensionless derived unit as it appears in the International System of Units (SI), when in reality θ = 1 m/m = 1 and knowing θ = 1, the angle measures β = 1 rad. In the formula s = θ • r the variable θ is a dimensionless variable, it is a number without units, it is the number of radians. When confusing what θ represents in the formula, some mistakes are made in Physics in the units of certain quantities, such as angular speed. My guess is that actually the angular speed ω is not measured in rad/s but in (rad/rad)/s = 1/s = s^(-1).
At minute 0:55 you calculate θ by substituting the arc and radius lengths in the formula θ = s / r θ = (50 m) / (25 m) θ = 2 rad. Actually the result is θ = 2 since θ is a dimensionless variable in the formula, it is the “number of radians”, and the measure of the angle, let's call it β, is You believe like most of the scientific community and the International System of Units (SI) that θ is measured in radians. That is not true. I will write you another comment where I show how the formula is obtained and what the variables represent.
Great video!
why do you name video "how to evaluate natural logarithms" ? these formulas works for any other real positive number (except 1)
Not bad.
@Zach's Math Zone --
great trick thanks
square root of 68 is just 2sqrt(17)
sqrt(68) = sqrt( 4 * 17) = sqrt(4) * sqrt(17) = 2 * sqrt(17) - good find! The only thing I struggle with is how he calculates the fraction to be "double", e.g. from 8^2 to the approximation 2 * 8 as the fraction part.
@@frankoptis It is because the derivative of sqrt(x) is 1/(2*sqrt(x)). This approximation finds the tangent to a known point on the sqrt curve A: f(x) = sqrt(A) + (x-A) sqrt'(A) = sqrt(A) + (x-A)/(s*sqrt(A)). As such it works well for the examples given in the video that are just over a square number, and less well for values that are just under a square number (like 24 or 35). Those will have quite a bit more error.
If you’re going to calculate the square root by hand anyway, just use the square root algorithm.
is the square root algorithm involve those fraction a+b and a+2b and stuff? Not sure which one are you talking about.
Wow! Really informative and concise.
Thanks for watching!