
- Видео 10
- Просмотров 224 680
The Applied Maths Tutor
Добавлен 8 дек 2013
A one stop shop for (eventually) all your applied mathematical needs.
Feel free to submit questions or requests.
Feel free to submit questions or requests.
Curvilinear III Intrinsic N T Coordinates
This is part 3/3 of Curvilinear motion in which i cover the use and derivation of Intrinsic Coordinates.
Просмотров: 3 065
Видео
Curvilinear II Polar Coordinates
Просмотров 4,1 тыс.10 лет назад
This is video 2/3 on Curvilinear motion in which I introduce the use and derive the equations of motion using a polar coordinate system.
Curvilinear I Parametric
Просмотров 88410 лет назад
This is part 1/3 for curvilinear motion. In this video I use assume our y displacement and our x displacement are given by functions of time and we use these to find speed and acceleration at given time values
Resisted motion in a straight line - Air resistance
Просмотров 85710 лет назад
In this video I introduce using calculus to deal with forces that are a function of the object's velocity.
Equation of Trajectory - Kinematics
Просмотров 85 тыс.10 лет назад
In this video I derive the equation of trajectory and use it to find the range of trajectory and the maximum height obtained during this motion
1st Moment of Area/Centroid
Просмотров 69 тыс.10 лет назад
This video goes through a couple of examples of finding the centroid of simple composite shapes using both the arithmetic mean and arguments of symmetry
Second Moment of Area from 1st principles
Просмотров 50 тыс.10 лет назад
In this video I introduce the method of finding the second moments of area of basic shapes from first principles.
Differentiation from first principles - Calculus
Просмотров 11 тыс.10 лет назад
This video tries to explain where our simplified rules for differentiation come from. Deriving the result from first principles.
Kinematics - SUVAT
Просмотров 1,5 тыс.10 лет назад
In this video, I derive the 4 main SUVAT equations graphically. Note that this derivation requires no calculus knowledge.
Linear Simultaneous Equations
Просмотров 15910 лет назад
This video is a introduction to solving Linear Simultaneous Equations using both the Substitution and Elimination methods



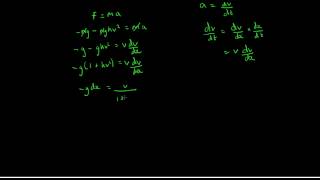





now i can calculate the trajectory of my piss at the urinal!
do you still post educational content somewhere? I find your teaching method of going into the whys of equations exceptionally helpful
Hello everyone from the past, present and future of year 12 ATAR Physics :)
I am going to use this in Bedwars
What I'm asking is how did the first formular come about. The integral of y squared d A
What is a "Tantitem" and a "Cosliter"?
if someone sees my comment by any change can you tell me how to apply this math if you already know the height that the object is being thrown at and the distance it travels
I don't know but I want to learn the capabilities of my mortar and how high and far and fast the shell will fly with a certain powder charge/gas seal and firing angle.
at max height the y component of the velocity will be 0; the distance it travels in x is the x component of the initial velocity times the time it takes for the object to fall down (height =0)
in this situation you could use the equation he made at around 4:15, replace y with the height the max height that you said you already know and replace x with 1/2 of the distance it travels and then finally solve for u to get the initial velocity.
@@fallaway-lol he mentioned he only knows the maximum height and the total distance travelled. He probably wants to find the initial velocity.
Ok but how about the reverse kinematics?
So good
Thank You!
Thanks
Math ia type beat
I'm in 8th grade why am I here.
Great explanation and use of the local extrema! Love these tutorials and breaking equations down into what they symbolize.
legend
my brain goes this can't work in case you throw the object in dir zenith, as this would require you to divide with something that could be zero, at which point the term for t can't be valid either. Which im guessing i why i remember the problem from highschool described as "sloped throw", please enlighten me if I am forgetting or missing something.
thank you sir
Consider to use the program POLYGONS to calculate and verify easy all this properties of triangles and polygons (moments of inertia, principal moments of inertia, product of inertia, centroid and more) -> jamarana.com/polygons
Great Great Thanks for video and Great explanation. Once more Great Thanks. Applying above logic in opencv
I'm the 600 sub
This is the best method for derivation of the trajectory formula!
thanks
Thanks
You're a fuckin beauty, bud. Great explanation.
I have been trying to work this out on my own--impressively presented. thanks!
Lol I’m in sixth grade and I still understood, good job and thx man!
thank you! amazing
who else is here a day before there exam XD
Thanks slot guys
Great explanation! Cheers
Excellent dude.....!
sir ,I have a. doubt there should be dy in place of dx and y in place of x because of the particular directions of x and y axis.when you will go in x direction the distance should me measured in terms of x and same for the y direction
Please consider the right axes.
How to consider the value of u ?
Not quite sure what you mean - u is the initial speed of the projectile, usually expressed in m/s.
I mean to say that how to find the value of initial velocity ?
It is a parameter, just like the initial angle, theta, and the gravitational field strength, g. It will have to be provided or some other information provided in order to work it out. For example, if you were given the maximum height or maximum range, you could use these values to estimate the initial speed, u.
Think of it as how fast is the bullet (projectile) traveling the instant it leaves the gun. The bullets Initial Velocity (that's if we are talking about guns and bullets in our example). So the bigger or more powerful the gun fired, the faster the bullet will be traveling once it leave the gun. This info must be given to you before you can do any of these calculations. It can be calculated separately but you must know all the variables of Internal ballistics, like how much powder is in the bullet and how big the bullet is etc...etc. This type of callulation is a whole subject to its own.
If you want to consider the value of u that means you already took the shot or threw the stone, therefore, you should have a result of an experiment that gives you the horizontal distance, and from that variable, you can now talk about the initial velocity by simply calculating with your observational values.
You are wrong. The definition you gave is not for a centroid but for a centre of gravity. The centroid is the geometrical point of an object from which the object itself is equally distributed. If assumed that the density and gravitational field are constant throughout the object then yes, the centroid, the centre of gravity and the centre of mass coincide. But it-s not correct to define the centroid as you do in the beginning.
Although I agree that the centroid and centre of gravity are distinct, for students first learning these concepts (particularly those struggling with the intuition) equating these ideas allows access to solving related problems. The main application which utilises the centroid is that of structural mechanics, particularly bending of beams. And when students first approach these concepts they deal with isotropic beams that exist in uniform gravitational fields, in these, most common situations, the centroid and the centre of gravity are one and the same. Furthermore, any formulation which models objects from the real world is bounded by numerous assumptions and restrictions; and in my experience of teaching, particularly when students are first approaching these concepts, the fine details of these modelling assumptions can get between the student and the concept at hand. For example, would your extended definition be useful for dealing with composite material problems including fluids? Any problem can be abstracted to positions which cause the simple model we use to breakdown, do Newton's laws hold inside a black hole, for example? Or is the basic linear response of a spring valid for large deflections? Would a cubic model be better for that situation? The point is, that doesn't help the person who is struggling to grasp the concept of restoring forces or gravity or even finding the neutral axis of a structural beam. Finally, this is not a peer-reviewed paper published in a journal, it's a video to help students grasp an idea they may be struggling with. It's not a place for pedantry. It's a place for learning and helping and coming together.
You sir, are a legend.
great explanation dude.. Thumbs up!
what a theta?
Jean-Luc Belanger ikr xD
Theta is a Greek symbol used as a variable in mathematics and in this physics calculation Theta represents the angle of launch of the projectile, relative to the horizontal axis (X-axis). The angle is in units of degrees (0-360 degrees) and can be converted to radians.
the launch angle of the projectile .
Wow. Never really thought of how equations were formed until you walked through this. Looking at it makes sense but yeah, I don't think I'd be able to come up with that myself lol. Anyway, great vid; it was educational and well done.
how to deal with questions where one part of the figure lies below the X- axis ?
erripuku la cheppavu. nice broo
erripuku la cheppavu. nice broo
gr8 explanation man !
great explanation. is there one for centroid of volumes?
very helpful tutorial.
The tutor is very very WRONG . . .Why ? The Xs are not the same thing that the Ys. Teaching mixing them is a very huge mistake. . . . Everybody knows it. We aren't GENIOUS.
Genius #correction.
REEEEEEEEEEEE
is this video for university level
This is really cool! I've been trying to find something this detailed for a long time now.
Really good video. Thanks. I like the use of different colours, as it makes it easy go see what you are doing.
thank god umi looked for thus then trajectory from flash was everywhere
Thanks mate. Helpful stuff