
- Видео 9
- Просмотров 5 760
Solving Math Problems
Япония
Добавлен 16 фев 2022
solving math problems, especially geometry problems.
Please subscribe my channel!!
Please subscribe my channel!!
Find the area of the blue region 20250112
Solving geometric math problem.
"Find the area of the green region"
Add a line, find another shape.
"Find the area of the green region"
Add a line, find another shape.
Просмотров: 547
Видео
Find the area of the green region 20250105
Просмотров 32814 дней назад
Solving geometric math problem. "Find the area of the green region"
Find the area of the blue square Pythagorean Theorem Ver. 20241229
Просмотров 50721 день назад
Solving geometric math problem. "Find the area of the blue square" Using Pythagorean Theorem Version.
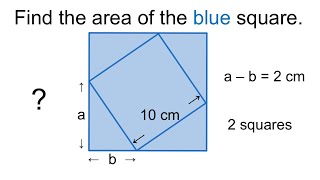
Find the area of the blue square 20241220
Просмотров 1,7 тыс.Месяц назад
Solving geometric math problem. "Find the area of the blue square" Add lines, find another square.
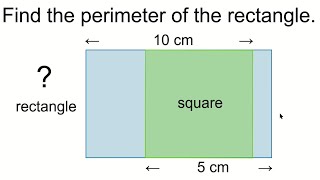
Find the perimeter of the rectangle 20241214
Просмотров 259Месяц назад
Solving geometric math problem. "Find the perimeter of the rectangle"
Find the area of the red region 20241125
Просмотров 4252 месяца назад
Solving geometric math problem. "Find the area of the red region" Find another shape with the same area.
Find the area of the red region;Trapezoid, Triangle
Просмотров 1,2 тыс.2 месяца назад
solving geometric math problem "Find the area of the red region" Find another shape with the same area.
Find the Area of the Shaded Region; 1 Square, 2 Semicircles, 1 quarter sector
Просмотров 2552 месяца назад
solving geometric math problem "Find the Area of the Shaded Region; 1 Square, 2 Semicircles, 1 quarter sector"
Find the Area of the Shaded Region; 2 Semicircles
Просмотров 6752 года назад
solving geometric math problem "find the area of the shaded region; 2 semicircles"







Area is 132
Yes
Good morning from PATRAS, GREECE. I saw your clever and more geometrical solution. My solution, i think, is more "learning" with using more Algebra. Let's name ABCD the given square and KLMN the green quadrilateral in which: AK=a, BL=b, CM=c and DN=d. Then AL=16-b, BM=16-c, CN=16-d and DK=16-a. Let's (X) the aria of KLMN. Then, (X)=(ABCD)-S (1) where S=the sum of the areas all the 4 right triangles. We know that (ABCD)= 16^2=256CM^2 (2) (AKL)=1/2[a(16-b)]=(16a-ab)/2. In the same way, (BLM)=(16b-bc)/2, (CMN)=(16c-cd)/2 and (DKN)=(16d-ad)/2. Adding S=(AKL)+(BLM)+(CMN)+(DKN)=...={16(a+b+c+d)+[(a+c)+(b+d)]}/2=> S=112cm^2 (3) So, replacing on (1) by (2), (3) we easily have (X)=144cm^2.
Thank you for your alternative solution. Yes, we can reach the summit by any route.
a = 2 + b (b+2)² + b² = 10² b² + 4b + 4 + b² = 100 2b² + 4b - 96 = 0 ∆ = 16 + 768 = 784 √784 = 28 -4 + 28 /4 = 6 b = 6 > a = 8 A = (6+8)² = 196 cm²
Algebraic vs. Geometric Solutions
To make it more simple, it is twice the area of the middle square minus the area of the small square, ie 2×10^2-2^2=196
I see
Thank you 😊
You're welcome 😊
A = 10 cm x 2 = 20 cm B = 5 cm x 2 = 10 cm Therefore, A + B = 20 cm + 10 cm = 30 cm
yes
Use Paithagorus theorem and common sense. 8+6=14 14x14=196 easy
Thank you for your comment. This video gives a solution that even an elementary school student can solve. The solution using Pythagoras theorum would be shown in the next video.
This is easy way to get answer means 14*14=196
100 (square inside is also blue)
exactly
Thanks
you're welcome