
- Видео 5
- Просмотров 562 936
Ben Gobler
США
Добавлен 22 авг 2021
Can you guess a shape from its shadows?
This video explores the question of whether you can determine the shape of a 3D object by observing a few of its shadows. The results are surprising and beautifully rich!
I created the slides in PowerPoint, and I wrote the music using a trial version of Ableton Live 11.
For more on this topic, here are some resources from Hideki Tsuiki (@hidekitsuiki1551) :
- Video showing the 3D prints and their various shadows (Watch This!): ruclips.net/video/VQvyxG4X4iA/видео.html
- Imaginary cubes webpage: u.kyoto-u.jp/icube
- Imaginary cube sculptures and Latin squares: archive.bridgesmathart.org/2010/bridges2010-159.html#gsc.tab=0
- Imaginary cubes and fractals: archive.bridgesmathart.org/2007/bridges...
I created the slides in PowerPoint, and I wrote the music using a trial version of Ableton Live 11.
For more on this topic, here are some resources from Hideki Tsuiki (@hidekitsuiki1551) :
- Video showing the 3D prints and their various shadows (Watch This!): ruclips.net/video/VQvyxG4X4iA/видео.html
- Imaginary cubes webpage: u.kyoto-u.jp/icube
- Imaginary cube sculptures and Latin squares: archive.bridgesmathart.org/2010/bridges2010-159.html#gsc.tab=0
- Imaginary cubes and fractals: archive.bridgesmathart.org/2007/bridges...
Просмотров: 558 235
Видео
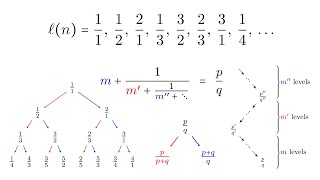
Listing the Rationals Using Continued Fractions Part 1
Просмотров 1,5 тыс.Год назад
This video motivates the series with a prompt: "Can you make a list of the rationals, where each number appears exactly once?" The Calkin-Wilf tree offers a surprisingly methodical way to make such a list. We learn that the rationals in the tree are organized by the Euclidean algorithm, which corresponds with the process of generating continued fractions. This connection produces a two-way algo...
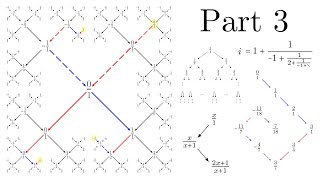
Listing the Rationals Using Continued Fractions Part 3
Просмотров 8102 года назад
In this video, we extend the Calkin-Wilf tree as fully as possible, and we study the properties of this new tree. For the third time, we improve our understanding of the golden ratio and the square root of 2 with a more sensible treatment of periodic paths. These paths have shocking consequences in the extended tree; we discover ordinary continued fractions for complex numbers, including the im...
Listing the Rationals Using Continued Fractions, Part 2
Просмотров 7322 года назад
This video provides rigor to the ideas from the first video. We verify the essential properties of the Calkin-Wilf tree, as well as its correspondence with continued fractions. Applications to irrational numbers are explored, including the golden ratio and the square root of 2, which become running examples in the series. Finally, we revisit an important case of the Euclidean algorithm relating...
[SoME1] Listing the Rationals Using Continued Fractions
Просмотров 1,6 тыс.3 года назад
This video was produced for the #SoME1 exposition in 2021. See the full series here: ruclips.net/p/PLWhQvrZCGE5IHCqO21zo75NEGOSTANmQN This video follows from a talk I gave in August 2021. The early elements of my method are attributed to work done by Jack Graver in his paper "Listing the Positive Rationals" - www.tandfonline.com/doi/pdf/10.1080/0025570X.2021.1843338 . The rest of the content- u...


![[SoME1] Listing the Rationals Using Continued Fractions](http://i.ytimg.com/vi/cSD3moYu3cs/mqdefault.jpg)
I want this sirpinsky triangle ! This is so tatisfaying
Click bait. This is all trivial and the geometry showed in the thumbnail is not even here. Dislike and move on.
the largest possible imgainary sphere is the tricylinder steinmetz solid.
what about the thumbnail?
Thumbnail problem - My answer is a cone with an infinitely thin square wall in the middle.
It's a chicken nugget
I feel like that one guy in Idiocracy
These shapes all go in the square hole.
I KNOW THE SHAPE FROM THE THUMBNAIL ITS A GUITAR AND ITS MUSIC WAS ELECTRIC
an imaginary sphere is an imaginary cube just in a sphere shape
it's like 1am, my first thought is that that might be interesting for crystallography.
Wow
First i came to thia video thinking it would be just a challenge video to guess shapes, but it turned out to be something a lot better, "i came here looking for Cooper but i ended with gold instead"
Amazing video! One interesting note is that the right rule on a fraction x can be stated as x+1. And the left rule has a similarly concise statement: x || 1, where "||" is the "parallel combination" operator, famously used in electric circuit analysis to find the total resistance of two resistors in parallel. By extension, m consecutive right moves can be stated as x + m, and m consecutive left moves as x || (1/m).
Looks like witchcraft 😂😂
Me thinking this was just a simple game: 🤡
Now just add another shadow
2:30 actually these shadows are wrong, (two of them should be stairs shaped like [][][] [][][] [][][]
There is a video game just about that called Viewpoint
5:40 Maybe the latin squares work because since each row and column have all the numbers, which means there isn't a gap on the shadows.
you could do the same process you did to the cube as the sphere i think, just imagine the sphere being in a cube
Another imaginary cube is an octahedron and the octahedron can be a fractal but it can’t possibly use cubes to make it
He never returned
Potato: I am shape 🥔
Very nice video :D
The initial picture i saw was basically the tip of a flathead.
Woah it's good a
You expected a cube, but it was me! The Sierpiński pyramid!
now for the imginary sphere pls
Damn. I was three months sober from fractals. I just wanted to watch an innocent video about shadows and finite shapes, and you just had to bring up fractals.
So, what's the answer of the thumbnail?
It’s a cylinder!
I do think that the serpinskis pyramid fractal making the square shadows is cool but something that I’m curious about is if it physically could make three perpendicular square shadows because from what I gathered, it’s shadow only makes a square when the light source is looking straight at the edge of the shape, but since none of the edges are perpendicular to eachother, I don’t think the serpinskis pyramid would actually be a solution to the 3 square shadow question (this is assuming that the light sources in the posed question are perpendicular to eachother). I may be wrong though and if I am I’d greatly appreciate if someone could correct me
Blues Clues for adults
7:59 Ball
This is tingling my autoCAD days.
Man, I woulda watched this sooner if the thumbnail was more accurate to the content. This was really good! That said, I do understand the grind.
If thats not a 7D spheroid from hell thats bull. 0:50
Brilliant work
I got the second one wrong, but called it a circular prism
This reminds me a lot of the illusion created by making 3D shapes that appear to say one word from a certain angle, and a different word from another angle. I believe those are constructed using Boolean geometry, usually, by creating the letters of one word in 3D and then subtracting the negative space of the letters of the other word from the shapes at a 90 degree angle.
dude i was here for the quiz :(
Oh... clickbait. 🤦
I literally figured this out with out watching the vid. i'd say that the q on the thumbnail is easy
Is it a triangular prism with a 2d circle on bottom? I'm so confused
@@amazingfireboy1848 no, think of a cone, with the flat facing down, then in the exact middle there is a flat square.
@@RobosaurasGolden That works too, although that still uses a 2d shape. I don't think there's an entirely 3d answer.
@@amazingfireboy1848 well, it would be 3d, just really flat
@@RobosaurasGolden I mean, it'd have to be EXTREMELY thin to not show up at the tip of the triangle shadow at all. But I guess if you want to be technical 🤷
when I saw the thumbnail I yelled peanut
This video has instantly become one of my favorite videos on the website. It's been a long time since I've ever been so baffled by something so simply complex. Love it, hope there's more in the future!
This video popped up after I had an after thought on my calculus classes last year about projections and parametrizations. And I do believe it would be such an interesting excercise just to go around doing the projection of random irregular objects
If 3D fractals can make square shadows… then is a Klein Bottle a three dimensional shadow of something arbitrarily more complex in the fourth dimension? My brain is hurting thinking of what fourth dimensional fractals would look like…
whatever it is, it fits in the square whole.
7:38 oh com on that joke was so *shady*