Видео

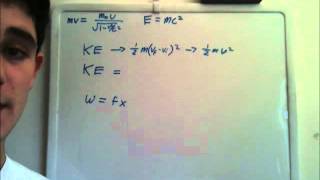
Big thumbs up to you. This helped me clear things up.

Thank You so much for you showed how Dr. Einstein did that and explained very clearly

Thank u, I totally understood it's derivation

thanks for clearing my doubts

just a little addition t = t' + vx'/(c^2)(how????) x'=x-vt dividing the whole equation by c x'/c=x/c-vt/c and as t=x/v or in this case t=x/c we get the result t = t' + vx'/(c^2)

Very nicely done! I wonder if this can extend to relativistic acceleration, i.e. a spaceship can accelerate at 1g to a distant star, but obviously cannot continue to do so because of the light speed barrier. How would we get a relativistic version of a=vt with an upper asymptote of c?

Advice: first prepare the stuff you want to present!

please first be confident yourself.don't upload such rubbish videos to confuse the other guys

I don't think that's what the word "derivation" means. The formulas just come falling out of the sky... It would have been interesting to see how Einstein's formulas follow from the principle of the constancy of the speed of light. (I have no idea about the answer, I'm not a physicist.)

Don't know if you read the comments on your videos, but why do you divide +- vx by c^2 every time?

Thanks dude! That was a huge help to me, keep up the good work.

Nice tutorial, why are you so smart?

you explain this really well. helps out a lot man, thanks.

Kinetic Energy=(1/2)mVf^2 - (1/2)mVi^2 Not (1/2)m(Vf-Vi)^2

Cool

exactly what i needed to know!! YOU´RE AWESOME!

where do you study dude?

I think there is a problem at 3:22 in the video. It assumes that the relativistic mass observed by A is the same before and after the collision: m1 u1 + m2 u2 = m1 v + m2 v. This is not the case since the observed mass depends on the observed velocity and the observed velocities are different before and after the collision.

thankyou sir

Please Upload other videos !!!!! I love you

How old are you ?

Thank you very much for such a smooth, logical proof. Your algebra skills are outstanding!

he did (C+V) for the light going in the direction the train is going, and (C-V) for the light traveling opposite the direction of the train (this V faster than C, and V slower than C)

This is the best explanation so far on youtube. Thanks a lot!

nice explained..

Are you sure this is the Lorentz Transformation for time? I thought it was t'=gamma(t-v*x/c^2)?

hi, could you please tell me how u derived the formula for t = t' + vx'/(c^2) etcetc at 4:35 please? thank you!

cheers man

thumbs up

I guess the only issue however with them coming to a complete stop would be the conservation of energy law would then be broken (unless the kinetic energy can be completely transferred to potential in some way I'm unaware of)

For this derivation, do we not have to assume that both m1 and m2 are identical in every way? If this is the case and they hit "head on" as your drawing shows, would they not just come to a complete stop given that the initial total momentum is zero (keeping in mind the assumption that the momentum is a vector, directed in the direction of velocity)? If you reference the Feynman Lectures on Physics he has another way of explaining it in chapter 16-4 Relativistic Mass

I need to learn Calculus HELP!!!

First, thanks for making this! What confuses me is that I'm not totally sure what's going on in the two reference frames. Is prime traveling away from nonprime towards the event? What exactly are x & x' and how do you derive the x= and x'= equations? Since x is the distance from non-prime's POV, and the time from non-prime's point of view is t, not t', so why is x = x' + vt' and not x = x' + vt ?

At 4:13 you have the two velocities inside the train as v+c and v-c. But I thought the speed of light was constant and you can't add/subtract from c

Brilliant video, very well explained :)

Great job explaining this.

Thanks for this, great video.

That was Awesome. Thank You.

I have a question for you. When you were taking the integral for KE, and you had: [Integral] vd(mv) Could you have done: [Integral] vd(p) Where the x-axis variable would be "dp" (Momentum)? I learned Calculus but this is the first time I have worked with Physics while doing Calculus. But i really appreciate these videos. Keep up the good work!

thanks for this-, makes more sense to me now :) one question though, why at around 9:30, did you use ∆t with L0 and ∆t0 with L, and not the other way around? :S