
- Видео 4
- Просмотров 109 819
OnePlusOneSpace
Великобритания
Добавлен 19 мар 2022
Hi! I'm interested in mathematical physics, and visualisation.
All animations are produced in python, using the community edition of Manim, the python library created by Grant Sanderson (a.k.a. 3Blue1Brown). Try it out here: www.manim.community/.
All animations are produced in python, using the community edition of Manim, the python library created by Grant Sanderson (a.k.a. 3Blue1Brown). Try it out here: www.manim.community/.
Invitation to Conformal Field Theory: Through the Looking Glass of Conformal Symmetry
At its simplest, a conformal field theory is a theory which has conformal symmetry (and is described in the language of fields). This video seeks to explain what conformal symmetry is, in visual terms, to provide an introduction to the rich theory of CFT.
0:00 Introduction
1:50 Why is conformal symmetry weird?
2:50 Conformal symmetry in the plane
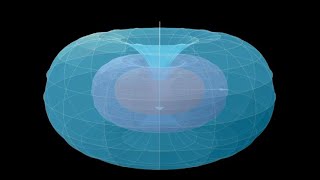
6:40 The conformally extended plane
8:00 Angles on spheres
10:30 Extended symmetry of the extended plane
Animations produced in Manim Community Edition.
0:00 Introduction
1:50 Why is conformal symmetry weird?
2:50 Conformal symmetry in the plane
6:40 The conformally extended plane
8:00 Angles on spheres
10:30 Extended symmetry of the extended plane
Animations produced in Manim Community Edition.
Просмотров: 26 620
Видео
Slicing bagels to learn gauge theory (Hopf fibration)
Просмотров 19 тыс.Год назад
Getting the perfect bagel slice is harder than it looks. Chapters: 0:00 Introduction 0:52 Basepoints and fibres 2:53 Three ways to slice a bagel 8:06 A taste of the mathematics of the Hopf fibration 11:38 Gauge theory Links: wikipedia: en.wikipedia.org/wiki/Hopf_fibration Niles Johnson's RUclips video: ruclips.net/video/AKotMPGFJYk/видео.html&ab_channel=NilesJohnson A nice set of notes (not min...
The well behaved infinity (Möbius maps and flows)
Просмотров 9 тыс.2 года назад
A fresh way to see spacetime symmetries. What makes an infinity well behaved? What does it mean to add together transformations? Chapters 0:00 Spacetime symmetries as Möbius maps 2:08 Stereographic projection/the point at infinity 3:27 Möbius maps 5:25 Even flow 7:02 x-rotations, complexly 8:00 Lost in translation 9:05 Epilogue This is an entry for a contest of Theories of Everything with Curt ...
The meme that teaches relativity (Spacetime symmetries and the celestial sphere)
Просмотров 55 тыс.2 года назад
Can a joke teach one of the most surprising aspects of relativity? How can we see four-dimensional transformations? What would we see if we accelerated to relativistic speeds? Mathematical jokes: en.wikipedia.org/wiki/Mathematical_joke Chapters: 0:00 The impossible triangle 1:11 Euclidean distance vs Pseudo-distance 2:43 Alice and Bob 3:30 Euclidean symmetries (in two dimensions) 4:35 Spacetime...



5:05 this is very good
I lived in New York, Troy - I know what a baggle is!
You mention other content on it, but honestly yours have been the most approachable by *far* that I've seen.
Brilliant video, by the way. I have no significant prior exposure to these ideas (other than the fact that I am just now belatedly trying to begin to explore quantum mechanics and quantum field theory beyond the "popularizations"), and yet your...illustrations (?) and explanations were entirely logical and clear. I'm sure I don't yet get more than a tiny fraction of the information being conveyed, but you've certainly piqued my curiosity and made me want to learn more.
"...sucked...into...a bagel."
I need more answers, what is the image of reality?
Mom: " Who the hell cut up all the bagels!" 🤣
This video helped me a lot and was fun to watch. Thanks. BTW,... A bread knife would've make thing much easier.
just seen the CFT video, cool visual
cool, excited for rhe 2nd part
Very cool!!!
very good!
Orbits (rotations) are dual to stabilizers (reflections) -- group theory. Two reflections give a rotation. "Always two there are" -- Yoda.
Space is dual to time -- Einstein. Space/time symmetries are dual to mobius maps. AdS is dual to CFT. Time dilation is dual to length contraction -- Einstein, special relativity. "Always two there are" -- Yoda.
I described the Hopf fibration to my teenage nephew. It helped that I'd previously shown him the game Hyperbolica. There's a level that takes place on the surface of a 3-Sphere.
the second life image at 14:01, that hopf fibration sculpture, is made by henry segerman www.youtube.com/@henryseg . and thx for mentioning of my site.
Is there some reason we don't visually represent the 3 sphere as a 2 sphere + its volume? The 4th coordinate (say, w) is the distance to the edge, or (1-r). The edge is w = 0, and the origin is w = 1. I guess w couldn't be negative; is that it, though? Just use a different color for -w.
A line is an infinitely large circle. What else would it be?
Very good video!!! I would like to put forward the idea that the sphere exists as in Huygens’ Principle of 1670 that says, “Every point on a light wave front has the potential for a new spherical 4πr² light wave". We can think of the point as a photon ∆E=hf. The spherical surface forms a boundary condition or manifold with light photon energy continuously transforming potential energy PE into kinetic Eₖ=½mv² energy of matter in the form of electrons. This form our ever-changing world with the movement of positive and negative charges. Because of the spherical geometry, we have to square the radius r² as in Ψ², t², e² and c².
Wonderful. Thank You.
This is awesome
Wait, so does the general unit circle have radius 0 then in the complex plane? Or does this 'meme' only say that for a 45 degree line out from the origin (an X centered at origin) ?
Only the X has a pseudo-distance of zero. In general a 'circle' with non-zero pseudo-distance is a hyperbola.
@@OnePlusOneSpace Thank you. Is there a name for this zero pseudo distance/spacetime way of looking at the complex plane? I know you say it's a meme but I can't find it. It seems really fascinating that the complex plane has this 45 degree speed of light sort of built into it! I'd like to learn more
It was actually the original formulation of Minkowski space (the technical name for spacetime), but later gave way to a formulation using only real coordinates, see here en.wikipedia.org/wiki/Minkowski_space#Complex_Minkowski_spacetime
@@OnePlusOneSpace Wow I had no idea, seems like Poincare was onto something with the 4d sphere... reminds me of Twistor space!
When you talk about transformations of the celestial sphere, would it be correct to identify that with vision itself? In other words, is the sequence of successive of light cones (celestial spheres) coming into our eyes EXCLUSIVELY Möbius transformations, of a spherical family of light rays/photons? Penrose starts his twistor lectures by giving the example of imagining oneself in deep space, and states the way the stars move is conformal as you move around. What I'm not clear on is whether this conformal mapping of light is true only at high/relativistic speeds without gravity/mass around, or whether it's a general truth about vision no matter where you are/what you're seeing.
Both Matter and Energy described as "Quanta" of Spatial Curvature. (A string is revealed to be a twisted cord when viewed up close.) Is there an alternative interpretation of "Asymptotic Freedom"? What if Quarks are actually made up of twisted tubes which become physically entangled with two other twisted tubes to produce a proton? Instead of the Strong Force being mediated by the constant exchange of gluons, it would be mediated by the physical entanglement of these twisted tubes. When only two twisted tubules are entangled, a meson is produced which is unstable and rapidly unwinds (decays) into something else. A proton would be analogous to three twisted rubber bands becoming entangled and the "Quarks" would be the places where the tubes are tangled together. The behavior would be the same as rubber balls (representing the Quarks) connected with twisted rubber bands being separated from each other or placed closer together producing the exact same phenomenon as "Asymptotic Freedom" in protons and neutrons. The force would become greater as the balls are separated, but the force would become less if the balls were placed closer together. Therefore, the gluon is a synthetic particle (zero mass, zero charge) invented to explain the Strong Force. An artificial Christmas tree can hold the ornaments in place, but it is not a real tree. String Theory was not a waste of time, because Geometry is the key to Math and Physics. However, can we describe Standard Model interactions using only one extra spatial dimension? What did some of the old clockmakers use to store the energy to power the clock? Was it a string or was it a spring? What if we describe subatomic particles as spatial curvature, instead of trying to describe General Relativity as being mediated by particles? Fixing the Standard Model with more particles is like trying to mend a torn fishing net with small rubber balls, instead of a piece of twisted twine. Quantum Entangled Twisted Tubules: “We are all agreed that your theory is crazy. The question which divides us is whether it is crazy enough to have a chance of being correct.” Neils Bohr (lecture on a theory of elementary particles given by Wolfgang Pauli in New York, c. 1957-8, in Scientific American vol. 199, no. 3, 1958) The following is meant to be a generalized framework for an extension of Kaluza-Klein Theory. Does it agree with some aspects of the “Twistor Theory” of Roger Penrose, and the work of Eric Weinstein on “Geometric Unity”, and the work of Dr. Lisa Randall on the possibility of one extra spatial dimension? During the early history of mankind, the twisting of fibers was used to produce thread, and this thread was used to produce fabrics. The twist of the thread is locked up within these fabrics. Is matter made up of twisted 3D-4D structures which store spatial curvature that we describe as “particles"? Are the twist cycles the "quanta" of Quantum Mechanics? When we draw a sine wave on a blackboard, we are representing spatial curvature. Does a photon transfer spatial curvature from one location to another? Wrap a piece of wire around a pencil and it can produce a 3D coil of wire, much like a spring. When viewed from the side it can look like a two-dimensional sine wave. You could coil the wire with either a right-hand twist, or with a left-hand twist. Could Planck's Constant be proportional to the twist cycles. A photon with a higher frequency has more energy. ( E=hf, More spatial curvature as the frequency increases = more Energy ). What if Quark/Gluons are actually made up of these twisted tubes which become entangled with other tubes to produce quarks where the tubes are entangled? (In the same way twisted electrical extension cords can become entangled.) Therefore, the gluons are a part of the quarks. Quarks cannot exist without gluons, and vice-versa. Mesons are made up of two entangled tubes (Quarks/Gluons), while protons and neutrons would be made up of three entangled tubes. (Quarks/Gluons) The "Color Charge" would be related to the XYZ coordinates (orientation) of entanglement. "Asymptotic Freedom", and "flux tubes" are logically based on this concept. The Dirac “belt trick” also reveals the concept of twist in the ½ spin of subatomic particles. If each twist cycle is proportional to h, we have identified the source of Quantum Mechanics as a consequence twist cycle geometry. Modern physicists say the Strong Force is mediated by a constant exchange of Gluons. The diagrams produced by some modern physicists actually represent the Strong Force like a spring connecting the two quarks. Asymptotic Freedom acts like real springs. Their drawing is actually more correct than their theory and matches perfectly to what I am saying in this model. You cannot separate the Gluons from the Quarks because they are a part of the same thing. The Quarks are the places where the Gluons are entangled with each other. Neutrinos would be made up of a twisted torus (like a twisted donut) within this model. The twist in the torus can either be Right-Hand or Left-Hand. Some twisted donuts can be larger than others, which can produce three different types of neutrinos. If a twisted tube winds up on one end and unwinds on the other end as it moves through space, this would help explain the “spin” of normal particles, and perhaps also the “Higgs Field”. However, if the end of the twisted tube joins to the other end of the twisted tube forming a twisted torus (neutrino), would this help explain “Parity Symmetry” violation in Beta Decay? Could the conversion of twist cycles to writhe cycles through the process of supercoiling help explain “neutrino oscillations”? Spatial curvature (mass) would be conserved, but the structure could change. ===================== Gravity is a result of a very small curvature imbalance within atoms. (This is why the force of gravity is so small.) Instead of attempting to explain matter as "particles", this concept attempts to explain matter more in the manner of our current understanding of the space-time curvature of gravity. If an electron has qualities of both a particle and a wave, it cannot be either one. It must be something else. Therefore, a "particle" is actually a structure which stores spatial curvature. Can an electron-positron pair (which are made up of opposite directions of twist) annihilate each other by unwinding into each other producing Gamma Ray photons? Does an electron travel through space like a threaded nut traveling down a threaded rod, with each twist cycle proportional to Planck’s Constant? Does it wind up on one end, while unwinding on the other end? Is this related to the Higgs field? Does this help explain the strange ½ spin of many subatomic particles? Does the 720 degree rotation of a 1/2 spin particle require at least one extra dimension? Alpha decay occurs when the two protons and two neutrons (which are bound together by entangled tubes), become un-entangled from the rest of the nucleons . Beta decay occurs when the tube of a down quark/gluon in a neutron becomes overtwisted and breaks producing a twisted torus (neutrino) and an up quark, and the ejected electron. The production of the torus may help explain the “Symmetry Violation” in Beta Decay, because one end of the broken tube section is connected to the other end of the tube produced, like a snake eating its tail. The phenomenon of Supercoiling involving twist and writhe cycles may reveal how overtwisted quarks can produce these new particles. The conversion of twists into writhes, and vice-versa, is an interesting process, which is also found in DNA molecules. Could the production of multiple writhe cycles help explain the three generations of quarks and neutrinos? If the twist cycles increase, the writhe cycles would also have a tendency to increase. Gamma photons are produced when a tube unwinds producing electromagnetic waves. ( Mass=1/Length ) The “Electric Charge” of electrons or positrons would be the result of one twist cycle being displayed at the 3D-4D surface interface of the particle. The physical entanglement of twisted tubes in quarks within protons and neutrons and mesons displays an overall external surface charge of an integer number. Because the neutrinos do not have open tube ends, (They are a twisted torus.) they have no overall electric charge. Within this model a black hole could represent a quantum of gravity, because it is one cycle of spatial gravitational curvature. Therefore, instead of a graviton being a subatomic particle it could be considered to be a black hole. The overall gravitational attraction would be caused by a very tiny curvature imbalance within atoms. In this model Alpha equals the compactification ratio within the twistor cone, which is approximately 1/137. 1= Hypertubule diameter at 4D interface 137= Cone’s larger end diameter at 3D interface where the photons are absorbed or emitted. The 4D twisted Hypertubule gets longer or shorter as twisting or untwisting occurs. (720 degrees per twist cycle.) How many neutrinos are left over from the Big Bang? They have a small mass, but they could be very large in number. Could this help explain Dark Matter? Why did Paul Dirac use the twist in a belt to help explain particle spin? Is Dirac’s belt trick related to this model? Is the “Quantum” unit based on twist cycles? I started out imagining a subatomic Einstein-Rosen Bridge whose internal surface is twisted with either a Right-Hand twist, or a Left-Hand twist producing a twisted 3D/4D membrane. This topological Soliton model grew out of that simple idea. I was also trying to imagine a way to stuff the curvature of a 3 D sine wave into subatomic particles. ==
It is fantastic. Thank you
Gaussian curvature preserves isometries but missed out on dilations. Maybe there is a curvature that preserves all conformal mappings?
I learned something from this; appreciate it! I'm not sure how far toward understanding Ads/CFT I might go though... This is just the baby step. There are earlier and simpler uses of conformal mapping, that solve useful problems in classical physics. One of the most famous ones arose very early in aerodynamics, where conformal mapping can transform a circle into an airfoil shape, and then the known solutions for a dipole plus a rotation can be mapped by this, to solve the airflow around the wing in the Euler flow approximation. This isn't physical because there is no drag. As a result an extra "trick" must be assumed: the rotation (and hence the lift) is specified so that the rear stagnation line does leave the cusp of the trailing edge. This approximation is about as far as analytic methods can take you in aerodynamics. . . The Navier Stokes equation being a bitch. It cannot get the drag at all, and cannot predict behavior near stall. But it does get the pressures over the wing surface pretty well. This plus Prandtl boundary layer scaling and a large body of empirical knowledge basically was the state of aerodynamics up through the 1930s
“A remarkable structure of nested tori”. Honestly, it’s just the same shape at different scales - we see this frequently in math. This topic couldn’t be more uninteresting. Outside of computer graphics, I don’t think fibers are useful in mathematics. Depends on what you consider to be basically a fiber though (is interpolation a fiber for example? because interpolation is necessary in calculus).
i am confused why the circles are tilted in 3D when you rotate them around z to obtain torus
This is an absolutely awesome video! Thanks for sharing your knowledge in such a digestible way. May I ask, how do you do those sleek animations?
Hey, thanks for the kind comment! I make my animations using the community edition of Manim, a free use python library based on a library developed by 3b1b.
Liked, subbed, and notifications set. Looking forward to part 2!
So you see how these EMF’s are organised like a Russian doll and they can all transmit information to each other. From the inner field to the outer fields and vice versa. You understand this now? So now understand that your brain makes an electro magnetic field like the ones you can see in this video; then understand that the earth also has one. The earths magnetic field is the one your brain is in and they both feed information back and forth. There is no way what so ever this is not the case because as physics will tell you. It is how it works. How this mechanism manifests is subject to question but it would explain some of the more abstract organic concepts that people come across when their brain is working in a particular way. This is perhaps something that your brain has evolved to filter out for the sake of surviving what is going on outside. The long and short of it is that your brain can function in a particular way but over time it has used this function less; however it does not mean it is completely overwritten. This function is like getting a shark that is normally hunting and flipping it on its back so it can relax and have a belly rub. You wouldn’t think it is possible. But it is.
Wonderful video. Thank you 🙏
[[ Obligatory geometric algebra comment (conformal geometric algebra)]]
5:00 looks like the equipotential surfaces of 2 infinite line charges
At 4:28 you say that compositions of translations, rotations and dilatations are the only (smooth) conformal mappings of the plane. This is not true, in 2D the conformal maps are the holomorphic (complex differentiable) functions with nonzero derivative. However, for dimensions greater than 2 a similar statement is correct! (Liouville’s theorem for conformal maps) I guess n>2 is the case we ultimately care about for physics, but unfortunately it’s much harder to visualize because of the 3-sphere required.
Anggap aja Allah yang lewat..❤
Astagfirullah gbs apa-apa.. modar!
Buktikan pd Allah, Yehuda kalo Einstein dkk satu genetika sama luh
Paling males gw jalur Yehuda. Lgsg abis otak gw
Hehe Jacobians.
My dad once used to say Science is simpled for not complexed.❤ I cannot go surfacing without my dad's assertation
Thank you for this video. It might be interesting for some to mention that while it is true that the described transformations are all transformations of the plane (2d flat space) and of the 2-sphere, there is a very interesting detour hiding here. As explained in the video, a conformal map is one which preserves angles. This is a local condition, for to find out what happens to any angle, you can (and have to) zoom in as far as you like into the angle. On the other hand, most (or, depending who you ask, all) maps we consider can be seen as being very nicely approximated by linear maps when you zoom in far enough. This is a generalisation of the derivative for functions \R -> \R, which also says that if you zoom in close enough, the function is roughly a line. For conformal transformations, this linear approximation then also has to preserve angles. In all dimensions, we understand well which linear transformations are conformal, i.e. preserve angles. In 2 dimensions, these turn out to be most maps (a bit more precisely: a linear transformation in 2 dimensions is given by 4 parameters, and a general conformal linear transformation is given by 2 parameters). However, in 3 and more dimensions dimensions, a smaller and smaller „portion“ of linear transformations is conformal (again more precisely: in 3 dimensions, a general linear transformation is given by 9 parameters, but a conformal linear transformation is given by only 4 parameters, and in 4 dimensions, the figures are 16 and 7 respectively - the number of parameters for conformal linear transformations is roughly half that for general linear transformations, but what counts is the absolute difference of the number of parameters). So in high dimensions, we might expect that requiring that the function should behave like a conformal linear map is a very strong restriction. This is indeed the case. Liouville‘s theorem states that a („nice“) conformal map defined on some subset of \R^n for n > 2 must in fact come from linear orthogonal transformations, translations, and „inversion“ (which is just one special map). But what about n = 2? Maybe it‘s not so bad in 2 dimensions? In fact, it is not. While conformal linear maps in 2 dimensions are much more restricted than general linear maps, there is a nice way to restate that restriction. It turns out (and this is in fact very easy to see when you look into the formulas) that you can view these linear approximations as complex numbers - so conformal maps defined on subsets of the plane may be viewed as maps from complex numbers to complex numbers which are locally approximated by complex numbers. These maps are called „complex differentiable“ maps. There’s quite a lot of them, and the study of them, complex analysis, is rich and beautiful. But how come then that there still only are few conformal transformations of the plane or the sphere? This is because while there are a lot of complex differentiable maps, their behaviour is very restricted in a lot of ways. For instance, a conformal transformation of the plane must be a complex differentiable map which is in addition injective (one-to-one). One can show that there are only few injective complex differentiable maps. That way, one recovers a version of the above Liouville theorem for dimension 2 (and although this requires one to develop some chunk of complex analysis, I‘d argue it‘s simpler than the Liouville theorem for high dimensions).
Upvoted just because you explained how the "physics" and "math" meanings are actually related. More critically, you lost me at the end. "do it upside down"? I don't see what the transformation was in the animation. A couple other things could be clearer.
completely unclear what the special transformation does
Worth noting that dilatations and rotations are not enough to produce all linear maps, and (in general) must center around the origin to be linear maps.
The most well known nonconformal transformation, while technically also a shearing, would be uneven scaling, aka stretching/squishing
Thank you very much for this great video! It has cleared up several questions that I have had about conformal field theory. Most resources I have found on this subject have been hard to understand. This one is a lot easier.