
- Видео 275
- Просмотров 131 369
finmath
Германия
Добавлен 25 апр 2020
Mathematical Models, Computational Finance
Lecture 2024-1 (43): Numerical Methods: American Monte-Carlo: Conditional Expectation in MC Sim(2/2)
Lecture 2024-1 (43): Numerical Methods: American Monte-Carlo: Conditional Expectation in MC Sim(2/2)
Просмотров: 211
Видео
Lecture 2024-1 (42): Numerical Methods: American Monte-Carlo: Conditional Expectation in MC Sim(1/2)
Просмотров 5755 месяцев назад
Lecture 2024-1 (42): Numerical Methods: American Monte-Carlo: Conditional Expectation in MC Sim(1/2)
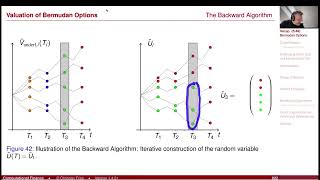
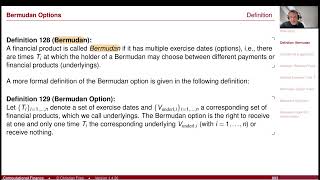
Lecture 2024-1 (41): Numerical Methods: Bermudan Options / American Monte-Carlo
Просмотров 2066 месяцев назад
Lecture 2024-1 (41): Numerical Methods: Bermudan Options / American Monte-Carlo
Lecture 2024-1 (40): Numerical Methods: Excursus: Density of the Underlying of a European Call Opt.
Просмотров 1776 месяцев назад
Lecture 2024-1 (40): Numerical Methods: Excursus: Density of the Underlying of a European Call Opt.
Lecture 2024-1 (39): Numerical Methods: Approx. of Partial Derivatives (3/3): Error Estimate
Просмотров 1226 месяцев назад
Lecture 2024-1 (39): Numerical Methods: Approx. of Partial Derivatives (3/3): Error Estimate
Lecture 2024-1 (38): Numerical Methods: Approx. of Partial Derivatives (2/3): Numerical Experiment
Просмотров 1666 месяцев назад
Lecture 2024-1 (38): Numerical Methods: Approx. of Partial Derivatives (2/3): Numerical Experiment
Lecture 2024-1 (37): Numerical Methods: Approx. of Partial Derivatives (1/3): Finite Differences
Просмотров 1246 месяцев назад
Lecture 2024-1 (37): Numerical Methods: Approx. of Partial Derivatives (1/3): Finite Differences
Lecture 2024 1 Session 26 - Poisson Process
Просмотров 1296 месяцев назад
Lecture 2024 1 Session 26 - Poisson Process
Lecture 2024 1 Session 36 - Control Variates
Просмотров 1706 месяцев назад
Lecture 2024 1 Session 36 - Control Variates
Lecture 2024-1 (22): Numerical Methods: Random Number Gen. (10): Acceptance Rejection Method (1)
Просмотров 1926 месяцев назад
Lecture 2024-1 (22): Numerical Methods: Random Number Gen. (10): Acceptance Rejection Method (1)
Lecture 2024-1 (21): Numerical Methods: Random Number Gen. (9): Other Distributions (3): Exponential
Просмотров 1567 месяцев назад
Lecture 2024-1 (21): Numerical Methods: Random Number Gen. (9): Other Distributions (3): Exponential
Lecture 2024-1 (20): Numerical Methods: Random Number Gen. (8): Other Distributions (2): Normal Dist
Просмотров 1347 месяцев назад
Lecture 2024-1 (20): Numerical Methods: Random Number Gen. (8): Other Distributions (2): Normal Dist
Lecture 2024-1 (19): Numerical Methods: Random Number Gen. (7): Other Distributions (1): ICDF Method
Просмотров 1677 месяцев назад
Lecture 2024-1 (19): Numerical Methods: Random Number Gen. (7): Other Distributions (1): ICDF Method
Lecture 2024-1 (16): Numerical Methods: Random Number Gen. (5): Low Discrepancy Seq. 2: Experiment
Просмотров 1277 месяцев назад
Lecture 2024-1 (16): Numerical Methods: Random Number Gen. (5): Low Discrepancy Seq. 2: Experiment
Lecture 2024-1 (17): Numerical Methods: Random Number Gen. (6): Low Discrepancy Seq. 3: Halton Seq.
Просмотров 1577 месяцев назад
Lecture 2024-1 (17): Numerical Methods: Random Number Gen. (6): Low Discrepancy Seq. 3: Halton Seq.
Lecture 2024-1 Session 15: Numerical Methods: Random Number Generation (4/5): Low Discrepancy Seq, 1
Просмотров 1268 месяцев назад
Lecture 2024-1 Session 15: Numerical Methods: Random Number Generation (4/5): Low Discrepancy Seq, 1
Lecture 2024-1 Session 14: Numerical Methods: Random Number Generation (3/5): Koksma-Hlawka Ineq.
Просмотров 1528 месяцев назад
Lecture 2024-1 Session 14: Numerical Methods: Random Number Generation (3/5): Koksma-Hlawka Ineq.
Lecture 2024-1 Session 13: Numerical Methods: Random Number Generation (2/5): Discrepancy
Просмотров 1188 месяцев назад
Lecture 2024-1 Session 13: Numerical Methods: Random Number Generation (2/5): Discrepancy
Lecture 2024-1 Session 12: Numerical Methods: Random Number Generation (1/5): Pseudo RNG
Просмотров 1808 месяцев назад
Lecture 2024-1 Session 12: Numerical Methods: Random Number Generation (1/5): Pseudo RNG
Lecture 2024-1 Session 11: Numerical Methods: Monte-Carlo Method (6/6): Monte-Carlo Integration 3/3
Просмотров 1608 месяцев назад
Lecture 2024-1 Session 11: Numerical Methods: Monte-Carlo Method (6/6): Monte-Carlo Integration 3/3
Lecture 2024-1 Session 10: Numerical Methods: Monte-Carlo Method (5/6): Monte-Carlo Integration 2/3
Просмотров 1448 месяцев назад
Lecture 2024-1 Session 10: Numerical Methods: Monte-Carlo Method (5/6): Monte-Carlo Integration 2/3
Lecture 2024-1 Session 09: Numerical Methods: Monte-Carlo Method (4/6): Monte-Carlo Integration 1/3
Просмотров 1728 месяцев назад
Lecture 2024-1 Session 09: Numerical Methods: Monte-Carlo Method (4/6): Monte-Carlo Integration 1/3
Lecture 2024-1 Session 08: Numerical Methods: Monte-Carlo Method (3/6)
Просмотров 2298 месяцев назад
Lecture 2024-1 Session 08: Numerical Methods: Monte-Carlo Method (3/6)





Vielen Dank!
Incredible lecture. Super clear! I'm doing my final project for a class exactly on weighted Monte-Carlo, so this is super helpful.
Thank you for making these videos available - They are brilliant
These have to be the two best lectures out there on American Monte Carlo algorithms. Explanations are clear, and the math behind it is solid! Thanks Professor.
Very interesting thanks
Thank you for the course, very intuitive.
I really love Christians work as well as Daniel Duffy’s.
Viele Grüße!
SPICY STUFF!
Thank you professor! Just navigated from your personal website. Appreciate all your work!
Thanks for sharing!
great video, thank you!
Thank you very much for posting the videos of the course on RUclips 👍🔥 Do you plan to update your book for a 2nd extended edition❓ ✔️I bought your book more then 13 years ago and I still read it today, there is no book equivalent on the market. ✔️At the same time the content of the videos on your RUclips channel is the best course I've ever seen. So I think a 2nd edition of your book with update from the new stuff in the videos would be a gift for everybody♥️🎁 🤗
Very good explanation
Great Lecture! Thank you for uploading this great lessons. There is still a question left: How do you interpret the value of the conditional expectation from the graphs on slide 783 shown at 47:00? I somehow do not get it, whereas it should be obvious.
Such great and lucid lecture series, making a complex topic simple! Thank you, Prof. Fries! Got to order your textbook.
0:24
12:49
7:23
33:57
It is a great lecture, may I ask if is there any repository to share the slides, please?
😍😍😍😍
Citadel and FTX sent me
Best course in RUclips thanks
Hello Professor, Could you please tell me which package you are using and if it is open source?
This is such a gem can't believe it has 912 views.
Great series Christian. Around 1:05:30 - is it fair to say that this is just a fully collateralized version of the put-call parity? So instead of a forward contract, you get the value of a collateralized forward (replicate by entering a repo)?
Many thanks for the very insightful content. Please what reading materials do you base your content on?
Amazing thank you so much.
There is one thing I don't understand: given any pair (T, K), I can either calculate sigma_loc(T, K) using Dupire's formula, or I can calculate sigma_iv(T, K) using Black-Scholes implied volatility function. In either case I will end up with a grid of volatilities which I then can interpolate to construct a volatility surface. So what exactly is the rationale for using Dupire instead of implied volatility?
sigma_iv(T,K) is the parameter sigma (a constant) you have to use in BS model to reproduce the value of that specific option C(T,,K). choosing this parameter the model will likely not reproduce the other option prices (they have different sigma_iv's). So there is no "one model" that reproduces all Europeans. (T,K) -> sigma_loc(T,K) is the surface you have to use in a Local Vol model to reproduce all option prices C(T,K) observed. So choosing just one point for one (T,K) is not sufficient. If the option prices observed were created with a single BS model you will find that sigma_loc(T,K) = sigma_bs (if sigma_loc is the local volatitliy in lognormal form). Hope this helps a bit. The two thinks are different quantities. Analogy: It like the velocity observed at a specific time compared to the average velocity oberserved up to a specific time. The two are related (one is an integral (average) over the other) and for constant velocity the two are the same.
Thank you for answering. I think I didn't ask the question clearly enough. I am not looking at the BS model, I am ONLY looking at the LV model dSt = r St dt + sigma(t, St) St dWt. My question relates to how we determine the sigma(t, St) given the market prices of a bunch of European call options. I can either use Dupire's formula to determine sigma_loc(T, K), or I can use BS implied volatility function to get sigma_iv(T, K). In either case I will end up with a grid of (varying) volatilities which reproduce the market prices and which I can then interpolate to construct sigma(t, St). But in both cases I want to use "one model", namely the local volatility model. I use BS only to determine the implied volatilities. So, my question is: why use Dupire if I can as well BS implied vols to determine sigma(t, St)?
@@fondueeundof3351 I am not 100% sure if I understand the question. If you interpolate sigma_iv(T,K) you have a kind of model to value all European options (just pick the corresponding sigma_iv(T,K) and plug it to BS formula, but you do not have a model for the stochastic process. The local volatility model is a model for the stochastic process S that would allow you to value - for example - an Asian option with a Monte-Carlo simulation,, where the model is consistent with the observed European options - so if you would use a Monte-Carlo simulation of S and value a European option, you will get the observed input prices (apart from numerical errors). Also: when interpolating local volatilities it is much easier to ensure absence of arbitrage. That said: if you are only interested in European option prices, a good (arbitrage-free) interpolation of BS volaitlites is an of course alternative (with possible advantages in performance or accuracy).
@@finmath6357 Ok I think I understand. I am looking at the stochastic process dSt = r St dt + sigma(t, St) St dWt, and am ONLY wondering how to estimate sigma(t, St) given market data. From your answer I gather that if I used BS impl vol function to determine the sigma(t, St), the resulting stochastic process would (probably) not reproduce the prices of the European calls that were used to calibrate the model, let alone price anything more exotic correctly. Thanks a lot for your time!
It was misleading to me denoting the gradient of f by J in 26:32, because in case f: R^n -> R we have J = gradient of f. And y-f(x) is just a scalar, not a vector, so there is no need to transpose it. Shame that the lecturer didnt mention that.
I see your point. The transpose is there to make it comparable to the "transposed" of (140). This transposed is there, because the gradient is a row-vector, not a column vector (as the Delta x). - But for m=1 that transposed is not needed - a column with 1 element is a row with one element. (It would be needed for m > 1 with f:R^n -> Rm). Thanks for the feedback. I try to improve this! Thank you.
@@finmath6357 Thank you for the anwser and thanks for your lectures, i love them! :)
@47:20: what about resampling W2 (or maybe W2 and W1) when in the next step V(t) would become negative?
Good question. One major disadvantage is, that resampling would be more complex from the implementation side. So instead: you could immediately sample a cut-of normal such that you do not require re-sampling. But then: The distribution we get from truncation and the distribution we get from reflection and the distribution we get from resampling, all have a bias. So you actually have to show if this bias improves the situation or if it makes it worse. And maybe it should be mentioned that the distribution we have to sample is known and it is possible to create an exact scheme, see Broadie and Kaya: www.columbia.edu/~mnb2/broadie/Assets/broadie_kaya_exact_sim_or_2006.pdf
@@finmath6357 Isn't sampling arguably the operation that is carried out most frequently in like an MC simulation, won't it therefore be highly efficient and shouldn't therefore an occasional resampling hardly impair performance? And also, truncation will introduce a discontinuity and reflection non-monotonicity, while resampling doesn't. That's why resampling might be preferable, but that's just my gutfeeling...
@@fondueeundof3351 I personally would not advice to do a resampling, because resampling also introduces some discontinuity and this discontinuity may be even worse: Assume you model parameters are such that V(t_i, omega_k) < 0. In that case you would trigger a resampling on this time step and path (t_i, omega_k). Now assume a change to the model parameters that will result in V(t_i, omega_k) >= 0. In the case you would not trigger a resamplling. Clearly, this is a discontinutity. The big problem is: if you use a 1-D random number generator to sample the 2-D factors, taking one more random number for the resample could result in a complete change of the random numbers for (dW1, dW2). - Of course, resampling is not completely forbidden, but one has be very careful (and there are better options).
@38:41: It's not clear to me how we get from mue in Feynman-Kac to rK in Dupire. Could you elaborate on this?
Yes. Maybe this should be elaborates in more detail. The rK corresponds to the mu = rS in the Feynman-Kac, where the K corresponds to the S. Of course: One had to proof this correspondence. The remark here is just for illustration that one could "guess" the formula. I am sorry for being not rigorous here..Maybe I should elaborate on this. (Christian)
Very nice lecture. Enjoyed learning the subtleties. Thank you!
Thank you.
Great lecture! Loved this
Beautiful lecture! Very clear exposition
Can I find the slides for these lectures?
Great explanation, thanks!
love your videos. Any chance you can upload the slides?
Great video. thanks you for making the time to make this video. The amount of work that is necessary to produce this content is quite impressive
Great video. the pace of explanation is right: the professor does not show off or try to impress. He just tries that we (the students) understand. Thanks for this generosity in taking the time to explain
Thank you, please can you give me a book or code for simulation
I am not 100% if I understand the request correctly. The derivation shown here is more or less taken from the book ISBN 978-0470047224. The simulation in shown there uses the code from www.finmath.net/finmath-lib/
Thank you very much
Thank you for the fantastic video. I have a question, ho wis r = log (1+ F.Delta T)/Delta T defined or derived?
👏
Will the professor covers the FMM - forward market model by mercurio and lyachenko? or does the professor think that their proposed generalization is not needed in practice? thanks so much
I am not (yet) covering it explicitly in this lecture, but the lecture on "The Short Period Bond" (Session 18 - ruclips.net/video/nu6LX7apbJI/видео.html ) is related. The extension is just that you "fill the gap" by simulating the short period bond (or the backward rate). If you are interested in having a model that allows to have finer (e.g. daily) tenors on the short end, you might also consider the time-homogenous forward rate model I have described here: papers.ssrn.com/sol3/papers.cfm?abstract_id=3664034 (this approach is actually a bit more general). I do not know if I will add a session on either one of the two this year, but if not, this is a good suggestion for next year! Thx.
Thank you for clear explanation on Quanto Adjustment factor through chosing domestic bond as numeraire.. I would try to derive through path for it.
Very thanks for kindly explanation of 5.Efficient implementation.
👊 ᵖʳᵒᵐᵒˢᵐ
LIKE 👍 👍👍 👍👍 👍 💌 💌 😻😻😻 😻😻😻
How do discussions of correlation apply to quasi random numbers?