
- Видео 244
- Просмотров 2 494
Allan Lind Jensen
Дания
Добавлен 11 окт 2011
problem 4-2-9 follow up
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms.
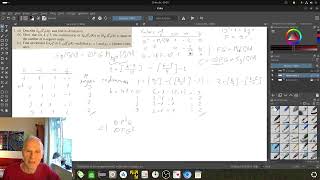
0:10 The class number of the number fields is related to the value of the L-function at s = 1. That ambition was ruled out from the onset. On the other hand, we become able to compute the values at 2 and -1.
6:00 I am using (2.15)
0:10 The class number of the number fields is related to the value of the L-function at s = 1. That ambition was ruled out from the onset. On the other hand, we become able to compute the values at 2 and -1.
6:00 I am using (2.15)
Просмотров: 33
Видео
problem 4-2-9
Просмотров 2214 дней назад
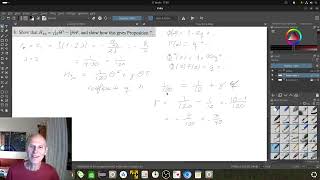
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. I cannot check the result for k = 7, because I don't know L(x_(-1), -2). But I will check k = 5 later.
problem 4 2 8
Просмотров 2314 дней назад
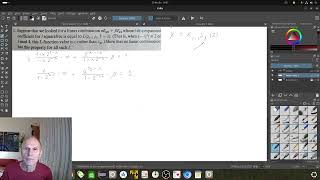
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. In my formula for number of ways to write n as a sum of 5 integers, then coefficient must be 20, and one should only sum over those n-j^2 that are odd. Off course, the formula only holds for n equivalent to 2 or 3 modulo 4. But I consider it a wo...
problem 4-2-7
Просмотров 1714 дней назад
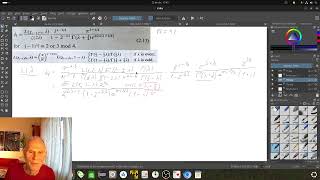
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. The formula for the Riemann zeta function, that I derive, turns out to be (23.2.15) in "Handbook of Mathematical Functions" by Abramowitz and Stegun. Unfortunately, we need the value at 1- 2 lambda. That is easy to correct.
problem 4-2-6
Просмотров 2921 день назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. I only prove the statement for l square-free. The general result follows from (2.33).
problem 4-2-5
Просмотров 1921 день назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. I failed to close the argument: There must be squarefree positive integers, such that (2/n) = -1 as well as 1.
problem 4-2-3 and 4
Просмотров 3021 день назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. Sorry, that I wrote a formula behind my head. Hope I didn't scare anybody.
problem 4-2-2
Просмотров 1421 день назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. 18:54 If you just wantto check your own results, compare with my display of the four cases here.
problem 4-2-1
Просмотров 828 дней назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. 14.00 I set k = 1 here. What happens, if we add 2 to the value of k? Then the result is multiplied by 1/4, still a positive number. 14.30 Not quite, rather 2^(-k/2) . 21.50 It is actually all of H that maps to the open, pierced unit circle.
Studying Chapter 4, Section 2
Просмотров 269Месяц назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. Studying Chapter 4, section 2 was hard. It led me to study the Gauss sums and reformulating the computations on page 188-9 and 195-8. This is a short presentation of the work, which can be downloaded from danishlightning.dk/al
problem 4-1-7
Просмотров 223 месяца назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. 16:07 Almost at once, I found problem 3-3-8a, so no coffee break to me. The sound was corrupted, while saying this; I cut it out. 19:01 It's not the last paragraph, but on page 182. It is shown that one can factor out q^(-r/h)
problem 4-1-6
Просмотров 433 месяца назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. The recording was marred by short bursts of white noise, which I deleted during editing. This ate some syllables, making some sentences more difficult to understand. If you wish, I can upload the document with my solution to my web-site.
problem 4-1-5
Просмотров 103 месяца назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. 04:03 Using the expansion at infinity and not the expansion at nought, sucks. We know that the sum of the order of zeroes of a form in M_2(Gamma_(4)) is unity. Every zero is a simple one, and the only one. 16:40 should be S_13/2(Gamma_0(4))
problem 4-1-4
Просмотров 113 месяца назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. 1:00 It should be f(\gamma z), of course. And j(\gamma,z) must be raised to -k. 3:00 I am comparing with the definition f(z)|[\gamma]_k from chapter 3. Did I mention that?
problem 4-1-3
Просмотров 63 месяца назад
This is part of the series of videos, where you can see a mathematician struggle with the problems of Neal Koblitz: Elliptic Curves and Modular Forms. At the end, I get for the cusp c = 0, that h = 4 and t = -i.





math without numbers looks like curse spell
Can u solve the discrete logarithm problem for koblitz curve?
I certainly can't. I will only try, if it comes up as a problem in the book; that would tell me, that it can be solved
@@allanlindjensen2306 if i may ask one more do you know anything about the 8 prime spirals?
p̾r̾o̾m̾o̾s̾m̾
I believe how you thought of taking sides 9,40,41 in the beginning is quite creative or a very smart guess. This is because guessing X,Y,Z for a given n is hard!.
Hi Truth, correct! I like working out explicit examples, always with a view to making the calculations easy.
Greetings Allan!! At 8:20 are you saying 4 divides (x^2+y^2) AND 4 divides (x^2-y^2)? But 4 divides u^2 does not imply 4 divides both. For example 4 divides 8x2=16 does not mean 4 divides 2 . We can say that 2 divides either (x^2+y^2) or (x^2-y^2).
Well done, Truth! I think I was looking at a case, where both x and y are odd, for instance x = 3 and y = 1. That example shows that you are right.
Thank you very much Sir. I am learning from this book and has started recently. Are you teaching this course or you are doing it for your own learning? Will you cover modular forms too?
Hi Truth. I thought my identity was visible to viewers, I am Allan Lind Jensen, allanl.jensen@gmail.com. Home page: danishlightning.dk/al Number Theory has always fascinated me; I am studying out of interest. It is my intention to cover the entire book - a project that seems to be taking three or four years. I have never in my entire life learned as much math as this last year!