
- Видео 18
- Просмотров 487 149
Numb3r Tr33
Италия
Добавлен 4 июн 2023
Numb3r Tr33 is all about visualizing the beauty of math.
Satisfying Space Filling Curves: 1D Becoming 2D
Here's a short compilation exclusively for fractal space filling curves, the most satisfying type of fractal.
Animation Tool: Manim library, Python
#maths #art #visualization #geometry #python #visual #satisfying #satisfyingvideo #algorithm #fractal #fractals #dragon #flowsnake #anklets #triangle #hilbert #fractalgeometry #coding #programming #visualprogramming #relaxing #manim
Animation Tool: Manim library, Python
#maths #art #visualization #geometry #python #visual #satisfying #satisfyingvideo #algorithm #fractal #fractals #dragon #flowsnake #anklets #triangle #hilbert #fractalgeometry #coding #programming #visualprogramming #relaxing #manim
Просмотров: 15 748
Видео
Turning Math Into Art With Amazing Fractals
Просмотров 62 тыс.Год назад
Here's the reloaded compilation of the algorithms used to obtain some of the most famous fractals, a clear example of how one can turn mathematics into art! #maths #art #visualization #geometry #python #visual #algorithm #fractal #fractals #dragon #tree #snowflake #hilbert #fractalgeometry #coding #programming #visualprogramming #relaxing #manim Visualization Tool: Manim library, Python
Turning Math Into Art With Beautiful Fractals
Просмотров 385 тыс.Год назад
Here's a compilation of the algorithms used to obtain the most famous and beautiful fractals, a clear example of how one can turn mathematics into art! #maths #art #visualization #geometry #python #visual #algorithm #fractal #fractals #dragon #tree #snowflake #hilbert #fractalgeometry #coding #programming #visualprogramming #relaxing #manim Visualization Tool: Manim library, Python
Top 3 Pythagorean Theorem Visualizations
Просмотров 2 тыс.Год назад
Here's the top 3 list of the Pythagorean theorem visualizations. These are the most immediate, clear and intuitive visualizations amongst the existing ones. #maths #visualization #geometry #python #visualproof #proof #pythagoras #theorem
Visual Proof for the Square and the Cube of a Binomial
Просмотров 2,4 тыс.Год назад
In this video two famous visual proofs to show where the square and the cube of a binomial come from. #maths #algebra #geometry #proof #visualization #visualproof #python Visualization tool: Manim library, Python
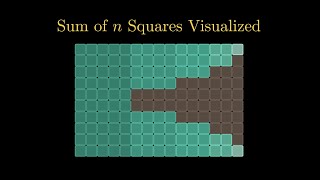
Visual Proof for the Sum of the First n Cubes
Просмотров 2,3 тыс.Год назад
Here's the famous visual proof for the sum of the squares of the first n natural numbers. #maths #numbertheory #algebra #geometry #visualization #visualproof #python Visualization tool: Manim library, Python
Hilarious New Proof for the Sum of the First n Squares
Просмотров 1,1 тыс.Год назад
This video shows a different way of finding the formula for the sum of n squares, through an alternative visualization. The process of proofing has been simplified in a non-rigorous way, in order to make the understanding of the concept smoother. The rigorous proof is coming soon in a paper that will be posted in the description of this video, for which I want to thank my best friend Luigi, who...
Visual Proof for the Sum of the First n Natural Numbers
Просмотров 1 тыс.Год назад
This is a short and sweet visualization of the famous Gauss formula, used to find the sum of the first n positive integers. #gaussian #formula #visualization #maths #algebra #geometry #numbertheory #python Visualization tool: Manim library, Python
Finding an Impossible Integral With Simulation
Просмотров 1,1 тыс.Год назад
Finding an Impossible Integral With Simulation
Law of Large Numbers - A Visual Intuition
Просмотров 775Год назад
Law of Large Numbers - A Visual Intuition








Sierpensi arrowhead curve - Sierpensi triangle
Snow 2:45
Love your videos - just a note on this one though, its 2D staying 2D, rather than 1D becoming 2D. The lines depicted have thickness ( a second dimension). If the lines were truly 1D (even if repeated infinite times) there would always be gaps between them. Imagine zooming in with every division, you'd notice the same amount of space between lines as when you started. Otherwise great stuff - nice music too
Hi! Actually I have to tell you, fractals have a weird geometry and when converging to infinity things change. Many fractals have a number of dimensions even irrational numbers, which is counter intuitive. If you search about fractal dimensions you'll find a lot of resources about it
Oh right - thank you, I didnt know about that @@Numb3rTr33
WOnderful
2:04 D4C
The "Fibonacci Snowflake" it starts with a ◆ and then multiplies but you can still see the ◆
This is why we have the Mona Lisa in squid games
Bentuk itu kayak buah
Bah kan lebih IMPOSSIBLE
Itu semua bentuknya IMPOSSIBLE
Numb3r Tr33 is a pythagorean tree😮
Mitsubishi 3:17
1:43 u just completed my childhood wishes. Always did those back in the copies wondering what it would look like but the copy never had a big space to it.
3:18 - Mitsubishi logo
I find it interesting that you can see Koch snowflakes within the hexaflake.
3:18 toyota 😂
there's like so much fractals I have never seen or heard like Photagrean tree
The Levy curve would have been amazing to end on, as it would have been the outline of the tree.
interessant das die sierpinski kurve die aus einem sierpinski dreieck entsteht am ende wie ein sierpinski dreieck aussieht.
2:32 🔶 💠
1:20 Pythagorean Tree 345 looks like a human brain!
1:40 squid game 2:
Osteoporosis
Whats the name of the song?
3:17 Handa!
The hexa flake has infinite koch snow flakes inside it
3:17 Mitsubishi
Hilbert and Gosper were strangers in real life(im dont speak english, iam Brazilian. And, this a joke)
in hexaflake, i'm seeing koch snowflakes too
Fractals are awesome.
This video is great! Thanks a lot!
i forgot to put 2:06
that looks like the shape player from game inside a game
Mandelbrot set?
0:07 the best by far organ in the body
But writing fractals in Qbasic isn't easy...
One of the chapters is 3:14
What software is this?
Koch Curve 85 is giving me evangelion flashbacks
This video is the gate to heaven.
(2⁴+5⁴) - [(1/e)/α^(π/5)]^(5/φ) = 0 φ = 1,6180339887... golden ratio, e = 2,7182818284... (Napier's constant, Euler's number), α = 0,0072973525677... (fine-structure constant)
4:20 umm familiar shape???🇩🇪
Wow so funny
2:36 oh hey, PK Freeze alpha
domain expansion: sierpinski triangle 1:10 transforms into sierpinski triangle 1:28
❤😊
They look peculiar
The hexafalke starts with a hexagon…
2:14 H fractal
Me: Spell Red Dummy: Red? L S T E R Me: What color is A Carrot? Dummy: I think It Is Umm… I Think It’s Uhhhhh… I think it’s A Carrot Uhmmm… Idk about Carrots (idk about carrots) Me: If you dig a 6ft Hole, how Deep is That Hole? Dummy: Uhh… 20ft. GET- Me: … 1 - 1 = ? Dummy: Equals? 35 Me: (I Give Up)
i hate the fact that you're not famous enough! this has to get more fame but youtube does its thing to push content creators like you far back :(